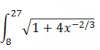-
Hola!
Alguien me ayuda con esto por favor?? Mañana tengo examen!!!
--------- ---------
2√ x - 1 = √ x + 6 +2
Antonio Silvio Palmitano
el 27/9/18Observa que los argumentos de las raíces cuadradas deben ser mayores o iguales que cero.
Luego, elevas al cuadrado en ambos miembros, y queda:
( 2*√(x-1) )2 = ( √(x+6) + 2 )2,
distribuyes la potencia en el primer miembro, desarrollas el cuadrado de una suma en el segundo miembro, y queda:
4*(x-1) = ( √(x+6) )2 + 4*√(x+6) + 4,
distribuyes el primer miembro, simplificas raíz y potencia en el primer término del segundo miembro, y queda:
4*x - 4 = x+6 + 4*√(x+6) + 4,
restas x y restas 10 en ambos miembros, y queda:
3*x - 14 = 4*√(x+6),
elevas al cuadrado en ambos miembros, y queda:
(3*x - 14)2 = ( 4*√(x+6) )2,
desarrollas el binomio elevado al cuadrado en el primer miembro, distribuyes la potencia en el segundo miembro (observa que simplificamos raíz y potencia en su segundo factor), y queda:
9*x2 - 84*x + 196 = 16*(x+6),
distribuyes el segundo miembro, y queda
9*x2 - 84*x + 196 = 16*x + 96,
restas 16*x y restas 96 en ambos miembros, y queda:
9*x2 - 100*x + 100 = 0,
que es una ecuación polinómica cuadrática, cuyas soluciones son:
x1 = 10/9.
x2 = 10,
y observa que las dos soluciones son válidas, ya que los dos valores no indeterminan a las raíces que tienes en los términos de la ecuación de tu enunciado.
Espero haberte ayudado.
-
aplicando el binomio de newton calcula (3ײ - ×)10
??????
Antonio Silvio Palmitano
el 27/9/18Recuerda la Fórmula de Newton para el desarrollo de un binomio elevado a una potencia cuyo exponente es un número natural:
(a + b)n = ∑(k=0,n) C(n,k)*ak*bn-k (1).
Luego, tienes los datos en la expresión de tu enunciado:
a = 3x2 (primer término del binomio),
b = -1x (segundo término del binomio),
n = 10 (exponente de la potencia);
luego, sustituyes expresiones en la Fórmula de Newton señalada (1), y queda:
(3x2 - 1x)10 =
= ∑(k=0,10) C(10,k)*(3x2)k*(-1x)10-k =
distribuyes y resuelves el exponente en el segundo factor del argumento de la sumatoria, distribuyes el exponente en el último factor, y queda:
= ∑(k=0,10) C(10,k)*32*x2k*(-1)10-k*x10-k =
ordenas factores en el argumento de la sumatoria, y queda:
= ∑(k=0,10) (-1)10-k*32C(10,k)*x2k*x10-k =
resuelves el segundo factor, aplicas la propiedad de la multiplicación de potencias con bases iguales en el producto de los dos últimos factores, y queda:
= ∑(k=0,10) (-1)10-k*9*C(10,k)*xk+10,
que es la expresión del desarrollo de la expresión que tienes en tu enunciado.
Espero haberte ayudado.
-
Hola, ¿ alguien me puede ayudar a resolver esta integral por partes?
(x^2-2x) e^x
Antonio Silvio Palmitano
el 27/9/18Plantea el método, y tienes:
u = x2-2x, de donde tienes: du = (2x-2)*dx;
dv = ex, de donde tienes: v = ex.
Luego, aplicas el método (I = u*v - ∫ v*du), y la integral de la función cuya expresión tienes en tu enunciado, queda:
I = (x2-2x)*ex - ∫ ex*(2x-2)*dx.
Luego, planteas el método para la integral secundaria, y tienes:
u = 2x-2, de donde tienes: du = 2*dx;
dv = ex, de donde tienes: v = ex.
Luego, aplicas el método en la integral secundaria, y la integral de la función cuya expresión tienes en tu enunciado, queda
I = (x2-2x)*ex - ( (2x-2)*ex - ∫ ex*2*dx );
luego, distribuyes el agrupamiento, y la integral queda:
I = (x2-2x)*ex - (2x-2)*ex + ∫ ex*2*dx;
luego, extraes el factor constante en la integral terciaria, y queda
I = (x2-2x)*ex - (2x-2)*ex + 2*∫ ex*dx;
luego, resuelves la integral terciaria (observa que es directa), y queda:
I = (x2-2x)*ex - (2x-2)*ex + 2*ex + C;
luego, extraes factor común entre los tres primeros términos, y queda:
I = ( (x2-2x) - (2x-2) + 2 )*ex + C;
distribuyes y resuelves la expresión en el factor polinómico, y queda:
I = (x2-4x+4)*ex + C;
factorizas el trinomio cuadrado perfecto que tienes en el agrupamiento, y queda:
I = (x-2)2*ex + C.
Espero haberte ayudado.
-
Hola!!
Necesitaría ayuda con un problema de probabilidad condicional por favor:
Para empezar no sé ni cómo interpretar esa tabla, tal vez hay error o algo y la tabla la interpreto así :
Bueno, como sea necesito ayuda :/
gracias
Antonius Benedictus
el 27/9/18Antonio Silvio Palmitano
el 27/9/18Yo entiendo que la tabla es de doble entrada, y que las cuatro cantidades corresponden a las probabilidades de las intersecciones:
p(Hs ∩ Ms) = 0,22,
p(Hs ∩ Mns) = 0,24,
p(Hns ∩ Ms) = 0,31,
p(Hns ∩ Mns) = 0,23.
Observa que tienes para los sucesos individuales:
p(Hs) = p(Hs ∩ Ms) + p(Hs ∩ Mns) = 0,22 + 0,24 = 0,46,
p(Hns) = p(Hns ∩ Ms) + p(Hns ∩ Mns) = 0,31 + 0,23 = 0,54,
y observa que la suma de ambas probabilidades es igual a uno;
p(Ms) = p(Hs ∩ Ms) + p(Hns ∩ Ms) = 0,22 + 0,31 = 0,53,
p(Mns) = p(Hs ∩ Mns) + p(Hns ∩ Mns) = 0,24 + 0,23 = 0,47,
y observa que la suma de ambas probabilidades es igual a uno.
Luego, piden en tu enunciado:
p(Hs|Ms) = p(Hs ∩ Ms) / p(Ms) = 0,22 / 0,53 ≅ 0,42.
Espero haberte ayudado.