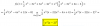-
Facu Imfeld
el 14/9/18Hola Unicoos....
f(x) = 2 - ∛(x-1)2
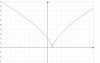
tengo que determinar máximos y/o mínimos de esa función
f`(x) = (-2/3)(x-1)-1/3
de acuerdo al procedimiento, al igualar f`(x) = 0, se obtiene como punto crítico x = 1
realizo la segunda derivada y obtengo
f``(x) = (2/9)(x-1)-4/3
y luego, se debería de evaluar el punto crítico obtenido, en la segunda derivada, si el signo resulta positivo, se trataría de un mínimo, si es negativo, se trataría de un máximo, pero como ven, al reemplazar x = 1 en la segunda derivada, se obtiene cero
si es un máximo o un mínimo se debería de poder apreciar un cambio de concavidad en la pendiente de la derivada , pero al darle un valor a izquierda de 1 y otro valor a derecha de 1, el signo de la pendiente se mantiene..
f``(0) = (2/9)(0-1)-4/3 = 2/9
f``(2) = (2/9)(2-1)-4/3 = 2/9
quisiera poder demostrar analíticamente que el punto es un máximo o un mínimo, pero aplico el contenido teórico y no llego a nada concluyente, no sé si tengo un error en este procedimiento o no. agradecería a quién pudiera demostrar si esta función tiene puntos críticos de manera analítica y no gráficamente. Gracias
Antonius Benedictus
el 14/9/18
Facu Imfeld
el 14/9/18 -
jorge gonzalez
el 14/9/18Saludos,
Por favor necesito ayuda para resolver este ejercicio de aljebra. El profesor dice que se hace con inversa y la solucion es
la imagen de abajo es la ecuacion.
Yauset Cabrera
el 15/9/18 -
coloso king
el 14/9/18Hola, ¿me podrian ayudar con este ejercicio de trigonometria?
Antonio Silvio Palmitano
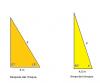
el 14/9/18
Observa las figuras, que son triángulos rectángulos cuyas bases corresponden a la sombra que hace el poste sobre el suelo, donde hemos indicado con p a la longitud de la hipotenusa que corresponde a la longitud del poste, y donde hemos indicado con α a la medida del ángulo de inclinación del poste con respecto al suelo antes del choque.
Luego, puedes plantear las relaciones:
cos(65°) = 5/p (1) (en el triángulo anaranjado),
cos(α) = 4,5/p (2) (en el triángulo amarillo).
Luego, multiplicas por p y divides por cos(65°) en ambos miembros de la ecuación señalada (1), y queda:
p = 5/cos(65°) (3), reemplazas valores, resuelves, y queda:
p ≅ 11,831 m.
Luego, multiplicas por p y divides por cos(α), y queda:
p = 4,5/cos(α) (4);
luego, igualas las expresiones señaladas (3) (4), y queda:
5/cos(65°) = 4,5/cos(α), multiplicas en ambos miembros por cos(65°)*cos(α), y queda:
5*cos(α) = 4,5*cos(65°), divides por 5 en ambos miembros, y queda:
cos(α) = 0,9*cos(65°), reemplazas valores, resuelves, y queda:
cos(α) ≅ 0,380, compones en ambos miembros con la función inversa del coseno, y queda:
α ≅ 67,644°.
Luego, planteas la expresión del ángulo de inclinación del poste con respecto al suelo, y queda:
Δα ≅ 65 - 67,644 ≅ -2,644°,
por lo que tienes que el ángulo de inclinación disminuyó 2,644° aproximadamente con respecto al ángulo de inclinación del poste antes del choque.
Espero haberte ayudado.
-
Alan Pariente
el 14/9/18 -
Guido Ferrari
el 14/9/18 -
Mariano Cornejo
el 14/9/18 -
Usuario eliminado
el 14/9/18 -
coloso king
el 14/9/18 -
José Carlos
el 14/9/18
Buenas, ¿me podeís ayudar en estos dos ejercicios?
Muchas gracias.
Antonius Benedictus
el 14/9/18¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
Mariano Cornejo
el 13/9/18Hola unicoos quería saber cómo resuelvo el ejercicio j), desde ya les agradezco.
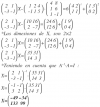
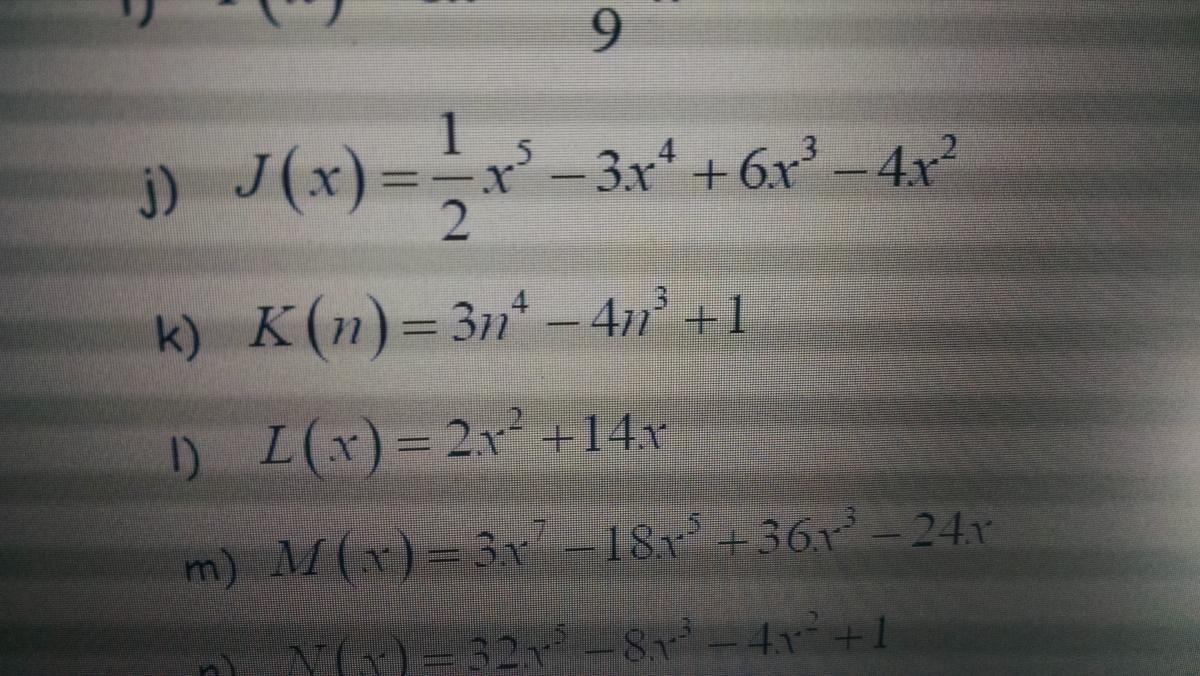Hola unicoos perdóneme por no entender, pero no puedo sacar factor común del punto j), gracias por la ayuda
