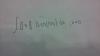-
Antonio Silvio Palmitano
el 11/9/18Observa que la primera función es continua en R, por ser una composición entre la función valor absoluto y una función polinómica, que son ambas continuas en el conjunto de los números reales.
Luego, planteas la condición de que su argumento sea mayor o igual que cero, y queda:
x2 - 4 ≥ 0, sumas 4 en ambos miembros, y queda:
x2 ≥ 4, extraes raíz cuadrada positiva en ambos miembros (observa que su índice es par), y queda:
|x| ≥ 2, que corresponde a las inecuaciones:
x ≤ -2 o x ≥ 2,
a las que les corresponde la expresión:
f(x) = x2 - 4, y observa que es válida para las condiciones: x < -2, x = -2, x = 2 y x > 2;
luego, por defecto, tienes que para las condición complementaria: -2 < x < 2, le corresponde la expresión: f(x) = -(x2 - 4);
y observa que los valores de corte son: x1 = -2 y x2 = 2.
Observa que la segunda función es continua en R, por ser una composición entre la función valor absoluto y una función polinómica, que son ambas continuas en el conjunto de los números reales.
Luego, planteas la condición de que su argumento sea mayor o igual que cero, y queda:
2x - x2 ≥ 0, sumas -1 en ambos miembros, y queda:
-1 + 2x - x2 ≥ -1, multiplicas por -1 en todos los términos de esta inecuación (observa que cambia la desigualdad), y queda:
1 - 2x + x2 ≤ 1, factorizas el trinomio cuadrado perfecto en el primer miembro, y queda:
(-1 + x)2 ≤ 1, extraes raíz cuadrada positiva en ambos miembros (observa que su índice es par), y queda:
|-1 + x| ≤ 1, que corresponde a la inecuación doble:-1 ≤ -1+ x ≤ 1, sumas 1 en los tres miembros de la inecuación doble, y queda la condición:
0 ≤ x ≤ 2,
a la que le corresponde la expresión:
g(x) = 2x - x2, y observa qe es válida para las condiciones: x = 0, 0 < x < 2 y x =2;
luego, por defecto, tienes que para las condiciones complementarias: x < 0 y x > 2, les corresponde la expresión: g(x) = -(2x - x2);
y observa que los valores de corte son: x3 = 0 y x2 = 2.
Luego, puedes plantear las expresiones de las dos funciones con todos los valores de corte expresados en particular, y quedan:
f(x) =
x2 - 4 si x < -2,
x2 - 4 si x = -2,
-(x2 - 4) si -2 < x < 0,
-(x2 - 4) si x = 0,
-(x2 - 4) si 0 < x < 2,
x2 - 4 si x = 2,
x2 - 4 si x > 2;
g(x) =
-(2x - x2) si x < -2,
-(2x - x2) si x = -2,
-(2x - x2) si -2 < x < 0,
2x - x2 si x = 0,
2x - x2 si 0 < x < 2,
2x - x2 si x = 2,
-(2x - x2) si x > 2.
Luego, sumas expresiones trozo a trozo, y la expresión de la función suma queda:
(f + g)(x) = f(x) + g(x) =
x2 - 4 - (2x - x2) si x < -2,
x2 - 4 - (2x - x2) si x = -2,
-(x2 - 4) - (2x - x2) si -2 < x < 0,
-(x2 - 4) + 2x - x2 si x = 0,
-(x2 - 4) + 2x - x2 si 0 < x < 2,
x2 - 4 + 2x - x2 si x = 2,
x2 - 4 - (2x - x2) si x > 2;
luego, distribuyes y reduces términos semejantes en las expresiones de los trozos, y queda:
(f + g)(x) =
2x2 - 2x - 4 si x < -2,
2x2 - 2x - 4 si x = -2,
-2x + 4 si -2 < x < 0,
-2x2 + 2x + 4 si x = 0,
-2x2 + 2x + 4 si 0 < x < 2,
2x - 4 si x = 2,
2x2 - 2x - 4 si x > 2;
luego, observa que puedes sintetizar las dos primeras condiciones, y también la cuarta con la quinta, y queda:
(f + g)(x) =
2x2 - 2x - 4 si x ≤ -2,
-2x + 4 si -2 < x < 0,
-2x2 + 2x + 4 si 0 ≤ x < 2,
2x - 4 si x = 2,
2x2 - 2x - 4 si x > 2.
Espero haberte ayudado.
-
¿Es lo mismo sen² x que sen x²? En caso de que no, además de qué diferencia hay me gustaría saber cómo se quitaría el cuadrado del primer miembro de las siguientes ecuaciones:
a) sen²x = (1 - cos x)/2
b) sen x² = (1- cos x)/2
-
Antonio Silvio Palmitano
el 12/9/18Comienza por operar en el numerador (N) y en el denominador (D) de la expresión por separado:
a)
N = 2-3*(-2)3*(-2)-3*(2*9)3*20,
aplicas la propiedad de la multiplicación de potencias con bases iguales en el segundo y el tercer factor, operas en el cuarto factor, resuelves el último factor, y queda:
N = 2-3*(-2)3-3*(2*32)3*1,
resuelves el exponente en el segundo factor, distribuyes el exponente en el tercer factor, y queda:
N = 2-3*(-2)0*23*(32)3*1,
resuelves el segundo factor, aplicas la propiedad de la potencia cuya base es otra potencia en el cuarto factor, y queda:
N = 2-3*1*23*36*1,
ordenas factores, y queda:
N = 2-3*23*36*1*1,
aplicas la propiedad de la multiplicación de potencias con bases iguales entre los dos primeros factores, y queda:
N = 2-3+3*36*1*1,
resuelves el exponente en el primer factor, y queda:
N = 20*36*1*1,
resuelves el primer factor, y queda:
N = 1*36*1*1,
resuelves la multiplicación del segundo factor por los otros tres factores que son neutros, y queda:
N = 36 (1).
b)
D = (3/2)-4*[(-3/2)3]2*(-3/2)-4*1-7,
aplicas la propiedad de una potencia cuya base es otra potencia en el segundo factor, resuelves el cuarto factor, y queda:
D = (3/2)-4*(-3/2)6*(-3/2)-4*1,
expresas a las bases del segundo y del tercer factor como multiplicaciones de -1 por un factor positivo, y queda:
D = (3/2)-4*(-1*3/2)6*(-1*3/2)-4*1,
distribuyes la potencia en el segundo y en el tercer factor, y queda:
D = (3/2)-4*(-1)6*(3/2)6*(-1)-4*(3/2)-4*1,
ordenas factores, y queda:
D = (3/2)-4*(3/2)6*(3/2)-4*(-1)6*(-1)-4*1,
aplicas la propiedad del la multiplicación de potencias con bases iguales entre los tres primeros factores, y entre el cuarto y el quinto factor, y queda.
D = (3/2)-4+6-4*(-1)6-4*1,
resuelves exponentes en los dos primeros factores, y queda:
D = (3/2)-2*(-1)2*1,
aplicas la propiedad de las potencias con exponente negativo en el primer factor, resuelves el segundo factor, y queda:
D = (2/3)2*1*1,
resuelves la multiplicación del primer factor por los otros dos factores que son neutros, y queda:
D = (2/3)2.
c)
Planteas la expresión formada por la división entre el numerador (N) y el denominador (D), y queda:
N/D =
sustituyes expresiones, y queda:
36 / (2/3)2 =
expresas al numerador en forma fraccionaria, distribuyes la potencia en el denominador, y queda:
= (36/1) / (22/32) =
resuelves la división entre expresiones fraccionarias, y queda:
= (36*32) / (1*22) =
aplicas la propiedad de la multiplicación de potencias con bases iguales en el numerador, resuelves la multiplicación en el denominador (observa que su primer factor es neutro), y queda:
= 38 / 22 =
resuelves el numerador y el denominador, y queda:
= 6561/4.
-
hola me podrian ayudar a entender interes compuesto ej: cual es el monto correspondiente a un capital de $120000 colocado a inters es compuesto al %12 anual, durante 2 1/2 , capitalizado semestralmente'?
otras preguntas: como : como se halla cuando preguntan Cual es el monto ? hallar el capital producido? a que tasa estuvo colocado?hallar el capital inicial? me dicen las formulas o ejemplos . otra pregunta como se saca cuando dice en meses cuatrimestres etc , ejemplo: capitalizacion cuatrismestral durante 4 años y 4 meses.
César
el 11/9/18 -
-
Buenas tardes, ¿ alguien me puede ayudar con las derivadas parciales de este sistema de ecuaciones?
f(x,y)=x(1- 0.01x -0.005y)
g(x,y)=0 .5y(1- 0.02y -0.02x)
Gracias
Antonio Silvio Palmitano
el 11/9/18Distribuyes en la expresión de la primera función, y queda:
f(x,y) = x - 0,01x2 - 0,005xy;
y observa que las expresiones de sus funciones derivadas parciales quedan:
fx(x,y) = 1 - 0,02x - 0,005y,
fy(x,y) = -0,005x.
Distribuyes en la expresión de la segunda función, y queda:
g(x,y) = 0,5y - 0,01y2 - 0,01xy;
y observa que las expresiones de sus funciones derivadas parciales quedan:
gx(x,y) = -0,01y,
gy(x,y) = 0,5 - 0,02y - 0,01x.
Espero haberte ayudado.