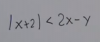-
Buenas tardes, se me ha presentado una duda con respecto al último apartado del siguiente ejercicio. Creo que se hace con producto escalar, por lo que he visto, pero no lo entiendo.

Antonio Silvio Palmitano
el 7/9/18Tienes la expresión de la función vectorial de posición:
r(t) = < t , (1/2)*t2 , t >;
luego derivas, y la expresión de la función velocidad queda:
r ' (t) = < 1 , t , 1 >,
cuyo módulo queda:
|r ' (t)| = √(2+t2) = (2+t2)1/2;
luego derivas la expresión de la función velocidad, y la expresión de la función aceleración queda:
r ' ' (t) = < 0 , 1 , 0 >.
Luego, planteas la expresión de la función vector tangente unitario, y queda:
T(t) = r ' (t) / |r ' (t)| = < 1/(2+t2)1/2 , t/(2+t2)1/2 , 1/(2+t2)1/2 > =
= < (2+t2)-1/2, t*(2+t2)-1/2 , (2+t2)-1/2 >.
Luego, ya tienes todo para plantear la expresión de la componente tangencial de la aceleración:
aT = r ' ' (t) ∗ T(t) = t*(2+t2)-1/2.
Luego, derivas la expresión del vector tangente unitario, y queda
T ' (t) = < -t*(2+t2)-3/2 , (2+t2)-1/2 - t2*(2+t2)-3/2 , -t*(2+t2)-3/2 >,
extraes factor común en la segunda componente, resuelves, y queda:
T ' (t) = < -t*(2+t2)-3/2 , 2*(2+t2)-3/2 , -t*(2+t2)-3/2 >,
cuyo módulo queda:
|T ' (t)| = √(t2*(2+t2)-3+4*(2+t2)-3+t2*(2+t2)-3) =
= √( (2*t2+4)*(2+t2)-3 ) = √( (2*t2+4) )*√( (2+t2)-3 ) = (2*t2+4)1/2*(2+t2)-3/2.
Luego, planteas la expresión de la función vector normal unitario, y queda
N(t) = T ' (t) / |T ' (t)| = < -t/(2*t2+4)1/2 , 2/(2*t2+4)1/2 , -t/(2*t2+4)1/2 >.
Luego, ya tienes todo para plantear la expresión de la componente normal de la aceleración:
aN = r ' ' (t) • N(t) = 2/(2*t2+4)1/2 = 2*(2*t2+4)-1/2.
Espero haberte ayudado.
-
Hola Unicoos, tengo el siguiente problema.
De un poste,se pinta la sexta parte de rojo;la cuarta parte,de verde;y los cuatro quintos de lo que queda,de azul.Si faltan pintar 7 metros,¿Cuánto mide el poste?
Saludos Cordiales
Yauset Cabrera
el 7/9/18
1/6 → va pintada de rojo,
1/4 → va pintada de verde,
A continuación, para hallar la proporción para el color azul, hemos de asumir la siguiente ecuación: 1/6 + 1/4 + x = 1, siendo x en este caso: lo que queda.
 Sin embargo, no nos olvidemos de un detalle: lo que va pintado son los 4/5 de x:
Sin embargo, no nos olvidemos de un detalle: lo que va pintado son los 4/5 de x: .
Por tanto, la proporción del poste que va pintada de azul es 7/15. Lo
restante, aplicando que la suma de las proporciones es igual a la
unidad: se corresponde con 7/60.Por tanto, aplicando reglas de tres:
7/60 → 7
7/15 → y ⇔x= (7/15 • 7) / (7/60) → y=28 metros
7/60 → 7
1/6 → z ⇔ z=(1/6 • 7) / (7/60) → z=10 metros
7/60 → 7
1/4 → φ ⇔ φ= (1/4 • 7)/(7/60) → φ=15 metros
Finalmente,
teniendo ya calculados los metros de las cantidades pintadas, lo que
mide realmente el poste, será la suma de todas las zonas:Longitud del poste = 7+y+z+φ ⇔ Longitud del poste = 60 metros
Espero haberte ayudado
Guillem De La Calle Vicente
el 7/9/18 -
Cuál es la asintota vertical, horizontal y oblicua de x+1/x
Antonio Silvio Palmitano
el 6/9/18Observa que si x toma valores muy grandes en valor absoluto, entonces tienes que el segundo término toma valores muy pequeños en valor absoluto, y que el primer término, por el contrario, toma valores muy grandes en valor absoluto. Por lo tanto, desprecias el segundo término, y queda la expresión:
y = x,
que es la ecuación de una asíntota oblicua de la gráfica de la función.
Si aplicas el mismo procedimiento, y llegas a una ecuación del tipo: y = constante, entonces tienes que esta ecuación corresponde a una asíntota horizontal, y recuerda que la gráfica de una función no puede tener a la vez asíntota oblicua y asíntota horizontal, ya sea para valores positivos muy grandes o para valores negativos muy grandes.
Luego, observa que el dominio de la función es: D = R - {0}, y observa que si consideras valores muy pequeños (muy próximos a cero) en valor absoluto, entonces tienes que el primer término toma valores muy pequeños, y que el segundo término toma valores muy grandes. Por lo tanto, tienes que la gráfica de la función tiene asíntota vertical cuya ecuación es:
x = 0.
Sería muy conveniente que recurras a un graficador para que puedas observar la gráfica de la función, junto con las gráficas de sus dos asíntotas.
Espero haberte ayudado.
-
Hola, una pregunta, a la hora de tener que discutir un sistema de ecuaciones según los parámetros A y B por el método de Gauss,
que me podeís aconsejar antes de empezar a reducir por Gauss, para que no se me complique el problema, para que sea más fácil, por ejemplo en que me baso para cambiar el orden de las filas o columnas.
A veces se me complica el ejercicio o se me hace muy largo y resulta que había otra forma de resolverlo muy corta.
Gracias de antemano.
-
Buenas días, me podrían ayudar con el problema 7 y 8 , bueno el 7 tengo una idea de como hacerlo con aritmética aplicando porcentajes pero hacerlo con derivadas no lo sé y bueno el 8 si estoy confundido, gracias.
Antonio Silvio Palmitano
el 6/9/187)
Observa que el hiperboloide es una superficie de nivel de la función diferenciable de tres variables cuya expesión es:
f(x,y,z) = z2 - 2x2 - 2y2,
cuya función vector gradiente tiene la expresión:
∇f(x,y,z) = < -4x , -4y , 2z >,
luego, evalúas para el punto en estudio: A(1,-1,4), y queda:
∇f(1,-1,4) = < -4 , 4 , 8 >,
que es un vector normal a la superficie en el punto en estudio.
Luego, con el punto en estudio y este vector, puedes plantear una ecuación del plano tangente, y también unas ecuaciones cartesianas paramétricas de la recta normal correspondiente (te dejo la tarea).
Espero haberte ayudado.
Antonio Silvio Palmitano
el 6/9/188)
Observa que la expresión del volumen del cilindro corresponde a una función diferenciable de dos variables, cuya expresión es:
V(R,H) = π*R2*H;
cuyas derivadas parciales tienen las expresiones:
VR(R,H) = 2π*R*H,
VH(R,H) = π*R2;
luego, planteas la expresión de su diferencial total, y queda:
dV = VR(R,H)*dR + VH(R,H)*dH,
sustituyes expresiones, y queda:
dV = 2π*R*H*dR + π*R2*dH.
Luego, tienes los datos:
R = 3 cm, H = 12 cm , dR ≅ +1 cm, dH = 0,
reemplazas valores, y queda:
dV ≅ 2π*3*12*1 + π*32*0 = 72π + 0 = +72π cm3,
por lo que puedes concluir que el volumen del cilindro aumenta aproximadamente la cantidad remarcada.
Espero haberte ayudado.
-
Me pueden ayudar con esta inecuación?
Es de un vídeo de unicoos que estaba escrita en la pizarra pero David no resolvió
Yauset Cabrera
el 6/9/18Vemos que podemos aplicar la propiedad de simetría |x|=|-x|. De esta manera, nos quedan dos inecuaciones a resolver:
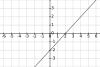
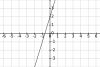
x+2<2x-y / -x-2<2x-y → Hemos de despejar y: x-2>y / 3x+2>y. Finalmente, representamos ambas funciones, como si de una igualdad se tratara: (Están en su orden correspondientes
Finalmente, escogemos un punto para cada función, que no pertenezca a la misma. Posteriormente, verificaremos la inecuación que nos había quedado...Para x-2>y, escogemos el punto (0,0), y sustituimos: -2>0 INECUACIÓN FALSA, significa que la solución a esta inecuación, es la región contraria al punto...
Para 3x+2>y, escogemos el punto (2,3), y sustituimos: 8>3 INECUACIÓN VERDADERA, significa que la solución es la región que contiene al punto...
Finalmente, la solución al ejercicio: será la intersección de ambas soluciones. Aquí te dejo la solución graficada:
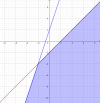
ESPERO HABERTE AYUDADO
-
Una consulta al realizar una división de polinomios, al tener el resultado del cociente y del resto, como acomodo esto nuevamente para proseguir con mi problema. La idea es tener el numerados con un grado menor, pero no comprendo que hacer cuando termino la división de polinomios












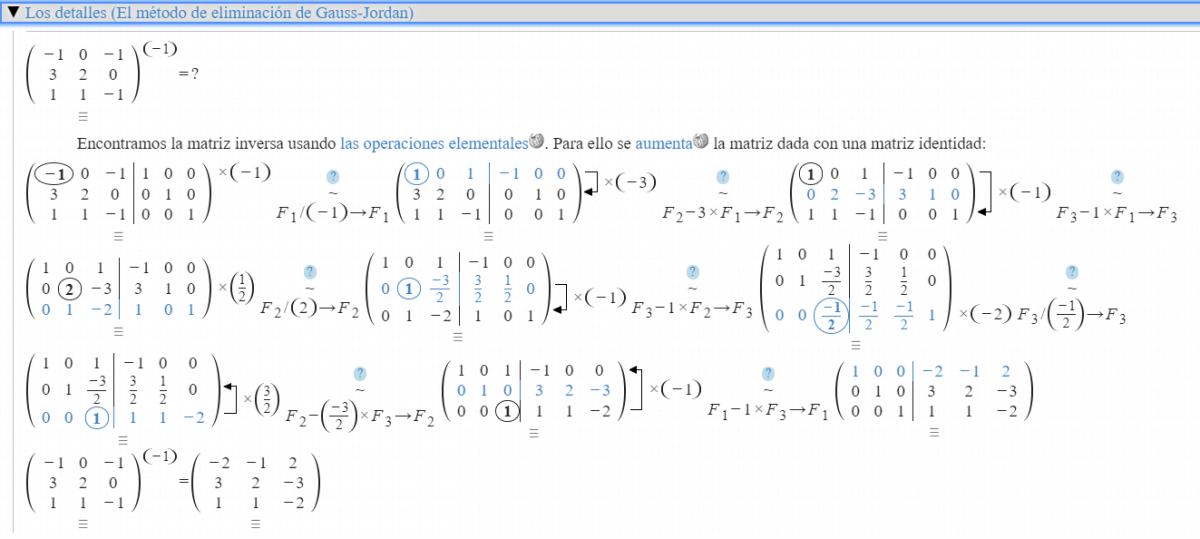


























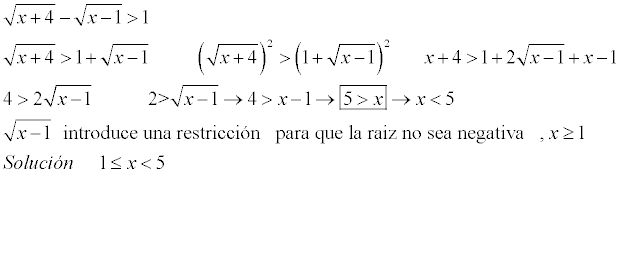 Casi la tenias
Casi la tenias