-
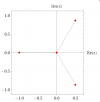
¿Qué explicación geométrica tiene que la integral de f(x)=1/x diverja y, sin embargo, la de g(x)=1/x2 converja a 1? ¿No deberían diverger las dos integrales puesto que ambas funciones poseen asíntotas en x=0 e y=0 y, por tanto, no deben encerrar ningún área?
Espero haberme explicado claramente. Un saludo.
César
el 4/9/18Diaz Daniel Victor
el 4/9/18Para empezar ¿Qué es una integral?
Una integral se la define como el Límite de la Sumatoria.
Si tomamos primero la sumatoria, podemos hablar de una serie, es decir la suma de una sucesión de números; Ya que estás hablando de las funciones tienen la forma 1/xp "Donde P es el exponente". Existen varias formas de demostrar que cuando P≤1 la serie diverge por lo tanto la integral también, por ejemplo, el método que utilizó Nicolas Oresme a través de la comparación... buscando una serie que sea mayor y que diverge, ya que por el teorema del sandwich o de compresión una serie que sea mayor que otra, que tenga la misma forma, va a tender al mismo límite osea si la primera converge la segunda también, en caso contrario ambas divergen.
Para las series que tienen a P>1 van a ser convergentes, ya que al ser el denominador cada vez mayor, la fracción tendrá menor valor, esto quiere decir que van a ir sumándose términos cada vez más chicos (de menor valor) llegando a un punto en donde al sumar el siguiente término no afectará a la suma total... al aplicar el límite este si existirá, a diferencia del caso anterior que sucede todo lo contrario.
Si estás habituado y leíste sobre esto creo que con la explicación intuitiva alcanza pero por si acaso te dejo unas fotos de un material donde está explicado es del libro Steward
Demostración de Oresme
Teorema de compresión
Serie P
José Carlos
el 4/9/18A ver si me ha quedado una cosa clara: ¿la integral de f(x) es equivalente a la serie cuyo término general es f(n)?
Por ejemplo, si f(x)=1/x, ¿la integral de 1/x es equivalente (por tanto el resultado es el mismo) que el sumatorio de 1/n?
PD: Quizás sea algo tremendamente obvio pero mis profesores no me lo llegaron a aclarar en ningún momento.
Diaz Daniel Victor
el 11/9/18Hola José perdón por la tardanza.
La integral nace de hacer la sumatoria y luego aplicarle el límite, es decir con la sumatoria solo encontras una suma parcial a n pero con el límite encontrás el valor exacto de esa suma. el signo de integrar es una s alargada debido a que la integral es el límite de una suma.
PD: Y sí esa sería la notación f(n)... pero como te dije uno da exacto y el otro no! Espero haber sido de ayuda! Por alguna duda me escribes a mi face Daniel V. Diaz
-
Antonius Benedictus
el 4/9/18Yauset Cabrera
el 4/9/18Aquí te dejo algunos recortes, que te ayudarán a calcular los dominios para el ejercicio 01:
En cuanto al ejercicio 02, lo más importante en cuanto a información, será calcular las asíntotas y los extremos locales de las funciones. Con eso y unos pocos puntos más, listo...
Aquí te dejo el primer ejercicio resuelto (con cálculos):
-
Ayuda, yo digo que da la D porque por las perpendiculares me queda que es un triangulo 45 45 90. La gente me dice que no es así, ¿está correcto?

-
Antonius Benedictus
el 4/9/18¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
Hola... me podrían ayudar a calcular el siguiente determinante, aplicando las propiedades de los determinantes... MIL GRACIAS
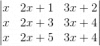
Antonio Silvio Palmitano
el 4/9/18Recuerda que a una fila le puedes sumar o restar un múltiplo de otra fila.
Luego, a la segunda fila le restas la primera, a la tercera fila le restas la primera, y el determinante de tu enunciado queda:
D =
x 2x+1 3x+2
0 2 2
0 4 2.
Recuerda que a una columna le puedes sumar o restar un múltiplo de otra columna.
Luego, a la segunda columna le restas el doble de la primera, a la tercera columna le restas el triple de la primera, y el determinante queda:
D =
x 1 2
0 2 2
0 4 2.
Recuerda que un factor común en una fila puede ser extraído como factor del determinante.
Luego, extraes factor común 2 en la segunda fila, extraes factor común 2 en la tercera fila, y el determinante queda:
D = 2*2*
x 1 2
0 1 1
0 2 1.
A la primera fila le restas la segunda, a la tercera fila le restas el doble de la segunda, y el determinante queda:
D = 2*2*
x 0 1
0 1 1
0 0 -1.
A la primera fila le sumas la tercera, a la segunda fila le sumas la tercera, y el determinante queda:
D = 2*2*
x 0 0
0 1 0
0 0 -1.
Recuerda que el determinante de una matriz diagonal es igual al producto de los elementos de su diagonal principal, por lo que el determinante de tu enunciado queda:
D = 2*2 * x*1*(-1) = -4*x.
Espero haberte ayudado.
-
Hola tengo una duda, me ayudan a resolver esto? No sé donde está mi error
4= (0,50+x)(050+x) (todo esto dividido entre) / (0,40-x) (0,40-x)
Lo tengo que hacer sí o sí utilizando la formula para resolver las ecuaciones de segundo grado me dio x=-0,10 y no veo mi error.
4= 0,25+0,5x+0,50x+x^2/ 0,16-0,40x-0,40x+x^2---> 4= x^1+1x+0,25/x^2-0,80x+0,16
3x^2 -4,2x + 0,39=0
Pero está mal y no veo mi error...
Gracias
:)
Antonio Silvio Palmitano
el 4/9/18Tienes la ecuación:
4 = (0,5+x)(0,5+x) / (0,4-x)(0,4-x) (observa que x no puede tomar el valor 0,4);
luego, multiplicas en ambos miembros por (0,4-x)(0,4-x), y queda:
4(0,4-x)(0,4-x) = (0,5+x)(0,5+x);
luego, distribuyes los dos últimos factores del primer miembro, distribuyes el segundo miembro, reduces términos semejantes, y queda:
4(0,16 - 0,8x + x2) = 0,25 + x + x2;
distribuyes el primer miembro, y queda:
0,64 - 3,2x + 4x2 = 0,25 + x + x2;
multiplicas por 100 en todos los términos de la ecuación, y quedA:
64 - 320x + 400x2 = 25 + 100x + 100x2;
restas 25, restas 100x y restas 100x2 en ambos miembros, reduces términos semejantes, y queda:
300x2 - 420x + 39 = 0;
divides por 3 en todos los términos de la ecuación, y queda:
100x2 - 140x + 13 = 0,
que es una ecuación polinómica cuadrática cuyas soluciones son:
x1 = (140 - 120)/200 = 20/200 = 1/10 = 0,1,
x2 = (140 + 120)/200 = 260/200 = 13/10 =1,3.
Espero haberte ayudado.
E
el 4/9/18Antonio Silvio Palmitano
el 4/9/18Cuando multiplicamos por cien en todos los términos de nuestra ecuación, lo hicimos para obtener coeficientes enteros, pero si prefieres puedes trabajar con coeficientes decimales.
Observa que restas 0,25, restas x y restas x2 en ambos miembros de tu ecuación, y queda:
3x2 - 4,2x + 0,39 = 0, divides por 3 en todos los términos de la ecuación, y queda:
x2 - 1,4x + 0,13 = 0, que es una ecuación polinómica cuadrática cuyas soluciones son: x1 = 0,1 y x2 = 1,3.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
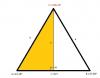
el 3/9/18Aplicas la propiedad de la suma de los ángulos interiores de un triángulo, y tienes para el ángulo faltante:
C = 180° - 24,16° - 47,66° = 108,18°.
Aplicas el Teorema del Seno en el triángulo ABC,y tienes:
sen(C) / c = sen(B) / b, de aquí despejas:
b = c*sen(B) / sen(C) = 8,4*sen(47,66°) / sen(108,18°) ≅ 6,535 millas.
Luego, tienes para el triángulo rectángulo AMC:
h/b = sen(A), de aquí despejas:
h = b*sen(A) ≅ 6,535*sen(24,16°) ≅ 2,675 millas,
que es el valor de altura del globo con respecto al suelo.
Espero haberte ayudado.