-
me podeis ayudar?
Encontrad las parametras "m" i "n" para que las rectas 2x +3y -2 =0 y x+my +n =0 sean:
a) paralelas b) perpendiculares c)una misma recta
Antonio Silvio Palmitano
el 2/9/18Tienes a las rectas presentadas por sus ecuaciones cartesianas implícitas.
Luego, despejas y en la expresión de la primera recta, y queda:
y = -(2/3)x + 2/3 (1),
y observa que su pendiente es: M1 = -2/3, y que su ordenada al origen es: N1 = 2/3.
Luego, despejas la expresión de la segunda recta, y queda:
y = -(1/m)x - n/m (2),
y observa que su pendiente queda expresada: M2 = -1/m, y que su ordenada al origen queda expresada: N2 = -n/m,
y observa que m debe tomar un valor distinto de cero.
Luego, planteas la condición de paralelismo (las pendientes de las rectas son iguales), y queda la ecuación:
M1 = M2, sustituyes expresiones, y queda:
-2/3 = -1/m, y de aquí despejas:
m = 3/2 (1);
luego, tienes dos casos para esta pendiente:
a)
las rectas son paralelas no coincidentes:
N2 ≠ N1, sustituyes expresiones, y queda:
-n/m = 2/3, multiplicas en ambos miembros por -m y queda:
n ≠ -(2/3)m, reemplazas el valor señalado (1), resuelve, y queda:
n ≠ -1,
por lo que tienes que las rectas son paralelas no coincidentes para: m = 3/2 y n ≠ -1;
c)
las rectas son paralelas coincidentes para m = 3/2 y n = -1.
b)
Planteas la condición de perpendicularidad (las pendientes de las rectas son contrarias y recíprocas), y queda la ecuación:
-1/M1 = M2, sustituyes expresiones, resuelves el primer miembro, y queda:
3/2 = -1/m, multiplicas en ambos miembros por 2m/3, y queda:
m = -2/3,
por lo que tienes que las rectas son perpendiculares para m = -2/3, y para cualquier valor real n.
Espero haberte ayudado.
-
 Me podríais ayudar a resolver este ejercicio, es q no me sale ni la continuidad ni la derivabilidad. Gracia!
Me podríais ayudar a resolver este ejercicio, es q no me sale ni la continuidad ni la derivabilidad. Gracia!Antonio Silvio Palmitano
el 2/9/18Observa que tienes la expresión en tres trozos de una función cuyo dominio es: D = R (observa que la expresión central se indetermina para x = 0, pero este valor no pertenece a su intervalo de definición).
Observa además que las expresiones de los tres trazos son continuas, por lo que tienes que los valores críticos a considerar son: x1 = 2 y x2 = 4, por lo que debes emplear la definición para estudiar la continuidad de la función para ellos.
a)
Continuidad en x1 = 2:
1°)
f(2) = 8/2 = 4;
2°)
Límites laterales:
Lím(x→2-) f(x) = Lím(x→2-) (3x - 2) = 3(2) - 2 = 6 - 2 = 4,
Lím(x→2+) f(x) = Lím(x→2+) (8/x) = 8/2 = 4,
por lo que tienes para el límite de la función:
Lím(x→2) f(x) = 4;
3°)
Como el valor de la función y su límite coinciden para este valor crítico, tienes que la función es continua en x1 = 2,
y podría ser derivable para este valor crítico.
b)
Continuidad en x2 = 4:
1°)
f(4) = 42 - 3(4) = 16 - 12 = 4;
2°)
Límites laterales:
Lím(x→2-) f(x) = Lím(x→2-) (8/x) = 8/4 = 2,
Lím(x→2+) f(x) = Lím(x→2+) (x2 - 3x) = 42 - 3(4) = 16 - 12 = 4,
por lo que tienes que los límites laterales no coinciden por lo que el límite de la función no existe para este valor crítico.
3°)
Como el límite de la función no existe para este valor crítico, tienes que la función no es continua en x2 = 4 y, por lo tanto,
tienes que la función no es derivable para este valor crítico.
c)
Planteas la expresión de la función derivada, y queda:
f ' (x) =
3 si x < 2,
a determinar si x = 2,
-8/x2 si 2 < x < 4,
no está definida si x = 4,
2x - 3 si x > 4;
luego, planteas los límites de las derivadas laterales para x1 = 2, y quedan:
Lím(x→2-) f ' (x) = Lím(x→2-) 3 = 3,
Lím(x→2+) f ' (x) = Lím(x→2+) -8/22 = -8/4 = -2,
y como los límites laterales de la función derivada no coinciden, puedes inferir que la función no es derivable en este valor crítico,
aunque debes aplicar la definición (te dejo la tarea) para mostrar claramente que las derivadas laterales son diferentes para x2 = 4.
Espero haberte ayudado.
Yauset Cabrera
el 2/9/18En sí, las funciones que constituyen a f(x), son continuas y derivables en R, por tanto: sólo hemos de fijarnos en los números en los que se producen el cambio de una función a otra. Me refiero a x=2, y x=4:
- Empezemos por x=2:
Evaluamos el lim x→2+f(x): si tenemos en cuenta que para x≥2, la función es 8/x → lim x→2+ 8/x=4
Evaluamos el lim x→2- f(x) = lim x→2- (3x-2)=4
∴lim x→2 f(x)=4. Ahora nos toca comprobar si este límite, se corresponde con la imagen de la función en x=2:
f(2)=8/2=4=lim x→2 f(x).
Por tanto, podemos confirmar que f(x) es continua en x=2...
- Vamos ahora con x=4
lim x→4+f(x) = lim x→4+(x2-3x) = 4
lim x→4- f(x)= lim x→4+(8/x)= 2
∴ lim x→4+f(x) ≠ lim x→4- f(x) → ∃lim x→4 f(x), lo que significa que f(x) no es continua en x=4
Ahora pasaremos a estudiar la derivabilidad de la función. Hallamos la función derivada de x:
f'(x)= | 3 si x<2
{ -8/x2 si 2≤x<4
| 2x-3 si x≥4
Concluimos con que f(x) es continua y derivable en R - {2,4}
f(x) no es continua y tampoco derivable en x=4
f(x) es continua pero no derivable en x=2, dado que f'(2+)≠f'(2-)
-
Hola! Podrías ayudarme a hacer este problema: el producto de dos números es 125. halla los números de forma que el cuadrado del primero más el doble sea mínimo
me he quedado atascado en xy=125
º x2 +2y=.....
Gracias de antemano!!!
Antonio Silvio Palmitano
el 2/9/18Observa que puedes despejar en tu primera ecuación:
y = 125/x (1) (observa que x no puede tomar el valor cero).
Observa que en tu segunda línea tienes la expresión de la función de dos variables:
f(x,y) = x2 + 2y.
Luego, sustituyes la expresión señalada (1) en la expresión de la función, resuelves el coeficiente del segundo término, y queda la expresión de la función de una variable:
f(x) = x2 + 250/x (2), cuyo dominio es: D = R - {0};
luego, planteas la expresión de la función derivada primera, y queda:
f ' (x) = 2x - 250/x2 (3) (observa que está definida en todo el dominio de la función);
luego, planteas la expresión de la función derivada segunda, y queda:
f ' ' (x) = 2 + 500/x3 (4) (observa que está definida en todo el dominio de la función).
Luego, planteas la condición de valor crítico (posible máximo o posible mínimo) de la función, y queda:
f ' (x) = 0, sustituyes la expresión señalada (3), y queda:
2x - 250/x2 = 0, multiplicas por x2 (observa que no toma el valor cero) y divides por 2 en todos los términos de esta ecuación, y queda:
x3 - 125 = 0, sumas 125 en ambos miembros, luego extraes raíz cúbica en ambos miembros, y queda:
x = 5, que pertenece al dominio de la función.
Luego, evalúas la expresión señalada (4) para el valor crítico remarcado, y tienes:
f ' ' (5) = 2 + 500/23 = 2 + 125/2 = 129/125 > 0,
por lo que tienes que la gráfica de la función es cóncava hacia arriba para el valor crítico, por lo que puedes concluir que este valor corresponde a un mínimo.
Luego, evalúas la expresión señalada (1) para el valor crítico, y queda: y = 25,
por lo que tienes que los números buscados son 5 y 25,
y observa que el valor mínimo de la función es (observa que reemplazamos el primer número en la expresión señalada (2) de la función):
f(5) = 52 + 250/5 = 25 + 25 = 50.
Espero haberte ayudado.
aversimesacoyaelbachiller
el 2/9/18Antonio Silvio Palmitano
el 2/9/18Tienes las ecuaciones cartesianas simétricas (o continuas) de la recta, y recuerda que tienes las componentes de un vector director en los denominadores de los miembros, por lo que puedes plantear que un vector director de la recta es:
u = < -1, 1 , 1 >, cuyo módulo es (te dejo la tarea del plantearlo y calcularlo): |u| = √(3).
Tienes una ecuación cartesiana implícita del plano, y recuerda que tienes las componentes de un vector normal en los coeficientes de los términos con incógnitas, por lo que puedes plantear que un vector normal al plano es:
n = < 1 , 1 , 1 >, cuyo módulo es (te dejo la tarea de plantearlo y calcularlo): |n| = √(3).
Luego, puedes plantear el producto escalar entre los dos vectores, y queda:
u • n = < -1, 1 , 1 > • < 1 , 1 , 1 > = -1 + 1 + 1 = 1.
Luego, planteas la expresión del producto escalar entre los vectores en función de sus módulos y del coseno del ángulo determinado por ellos, y queda:
|u|*|n|*cosθ = u • n,
divides en ambos miembros por |u|*|n|, y queda:
cosθ = u • n / |u|*|n|,
reemplazas valores, resuelves, y queda.
cosθ = 1/3,
compones en ambos miembros con la función inversa del coseno, y queda:
θ ≅ 70,529°, que es la medida del ángulo determinado por la recta y la dirección normal al plano.
Espero haberte ayudado.
-
Hola! Me podeis ayudar con el apartado c) y d)?
Consideramos las rectas : r: x=-1-3t
y=4+t
c) Encuentre el angulo que forma la recta r con el eje OY
d) Pertenecen el punto P(1,2) a la recta r? Y el punto Q(-4,5)? Justifique su respuesta.
-
Hola! ¿Cómo termino este ejercicio? Al pedirme la inversa de la matriz se refiere a la nueva o a la original del enunciado? Es el determinante correcto?
Gracias de antemano!!
Yauset Cabrera
el 2/9/18Hola de nuevo, se refiere a que determines si existe o no A-1.
¿De dónde sale la conclusión?, existe una fórmula simple, que si controlas los determinantes y la matrices en general; te recomiendo usar:
A-1=[adj(A)]t/|A|
-
Rubén
el 2/9/18En el ejercicio 14: a1+a2+a3=7
a4+a5+a6=56
Tienes que ver la relación que existe entre los dos números que conoces, el 7 y el 56, y te das cuenta de que el 56 es múltiplo de 7: 7 * 8 = 56; La solución sería (probando números teniendo cuenta que a1<a2<a3 al ser una progresión geométrica) 1+2+4=7, por la relación anterior la segunda ecuación quedaría 8+16+32=56. De ahí sabemos que a1=1 y que a4=8 por lo que a1+a4=1+8=9
-
Alejandro Ocaña Martín
el 2/9/18x² + (x+3)² < 29
x² + x² + 6x +9 < 29
2x² + 6x -20 <0
x1 = -5 ,x2 = 2
Comprueba que intervalo es válido
Intervalo válido: ( -5, 2)
Solución: como piden numeros naturales el intervalo se reduce a los números naturales, que son el 1, 2, 3...
La solución seria: 1 y 4. El caso de 2 y 5 no seria valido ya que al ser un intervalo abierto la suma de los cuadrados seria 29 y piden que sea menor que 29.
Espero que te ayude -
Hola! ¿Cómo termino este ejercicio? Al pedirme la inversa de la matriz se refiere a la nueva o a la original del enunciado? Es el determinante correcto?
Gracias de antemano!!
Daniel Pancorbo Delicado
el 1/9/18El apartado b seria: como el determinante de A es distinto de 0, A es invertible.
El determinante no lo tienes bien hecho, el procedimiento lo tienes bien pero se te ha olvidado hacer algo que hay que hacer cuando se usa ese método, fíjate en la primera división por 7.
Un saludo.
aversimesacoyaelbachiller
el 2/9/18Daniel Pancorbo Delicado
el 2/9/18Cuando usas este método, creo que se llamaba el de coefactores, cuando haces una operación en una linea tienes que hacer la operación contraria a la matriz. No me he explicado bien pero te pongo un ejemplo.
Si divides una fila por X (como has hecho en el primer caso) tienes que multiplicar la matriz por X. Y al revés, si multiplicas una fila por un numero, luego la matriz la tienes que dividir por ese mismo numero.
En tu caso, en el primer paso has dividido la dila entre 7, pues tienes que multiplicar toda la matriz por 7, de esta manera tienes que multiplicar por 7 el resultado que te ha dado y ya lo tendrías,
-
Buenas noches, a ver si alguien me puede echar una mano con este ejercicio, es un ejercicio de un examen de física pero es casi todo matemáticas.
He escrito al lado a boli el formula que creo que habría que usar, he intentado hacer la gradiente de B, una vez hecho eso integrar para eliminar la derivada y quedarnos con la E. Y cuando ya tenemos la E calculada de esta manera, igualarla con la que nos da el enunciado.
No se si el planteamiento está bien o si hay que hacerlo de alguna otra manera, pero no consigo sacarlo. Alguien me puede echar un cable?? Muchas gracias =)

























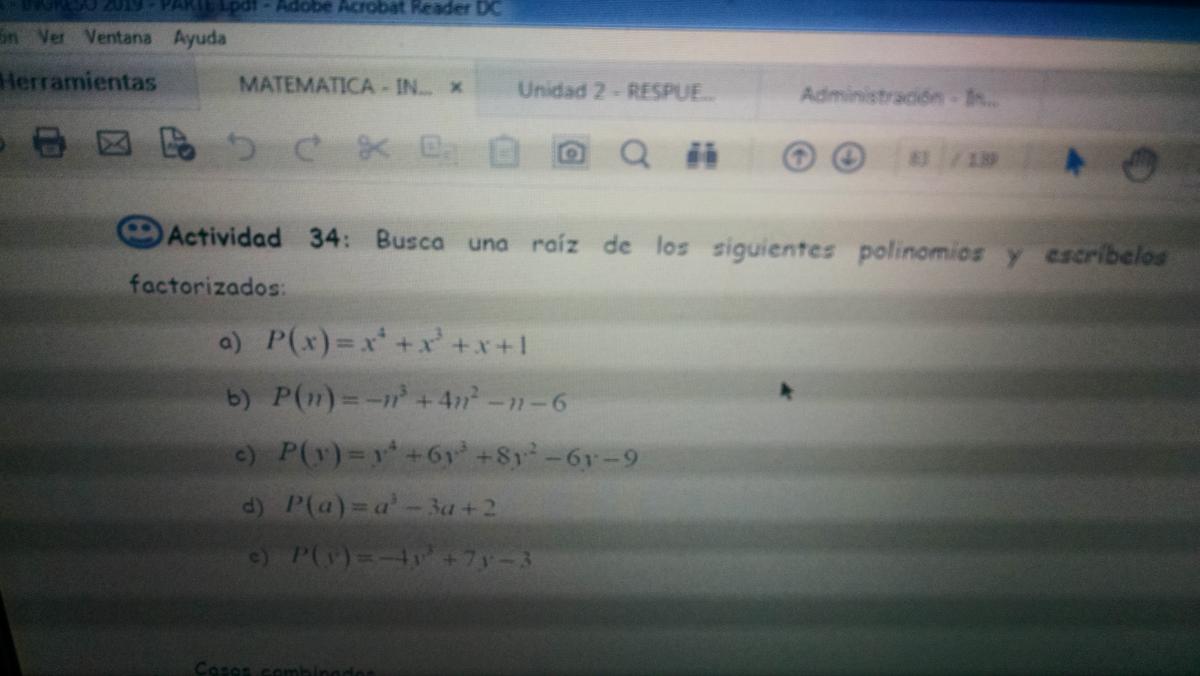 Hola unicoos quería saber cómo resuelvo el punto a), eso es todo, muchísimas gracias por la ayuda.
Hola unicoos quería saber cómo resuelvo el punto a), eso es todo, muchísimas gracias por la ayuda.










