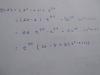¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que  lo entiendas.

Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).

Si los cálculos están bien hechos, sí. 

El procedimiento es correcto.

Te ayudo con la determinación del vector unitario dirección de máximo aumento de la temperatura.

Observa que la función temperatura es diferenciable en todo punto, por lo que planteas la expresión de su vector gradiente, y queda:

∇T(x,y) = < T_x , T_y > = < -4x , - 2y >;

luego, evalúas para el punto en estudio, y queda:

∇T(3,4) = < -12 , -8 >,

cuyo módulo queda expresado (te dejo el planteo y los cálculos):

|∇T(3,4)| = 4√(13).

Luego, planteas la expresión del vector unitario asociado al gradiente evaluado, y queda:

u = ∇T(3,4) / |∇T(3,4)| = < -12 , -8 > / 4√(13) = < -3/√(13) , -2/√(13) >,

que expresa la dirección de máximo aumento de la temperatura en el punto (3,4).

Espero haberte ayudado.

intuyo que la solución es correcta porque me dio lo mismo pero sin resolver al final, ya que lo deje en que cos²x=1

Has planteado correctamente la derivación, y solo quedaría que reduzcas el agrupamiento en tu última línea a su mínima expresión (observa que puedes distribuir el factor común 5, y luego reducir términos semejantes).

Espero haberte ayudado.

Has planteado correctamente las derivadas en ambos ejercicios.

Espero haberte ayudado.

a)

Observa que tienes la expresión de una función cuyo dominio es el conjunto de los números reales, observa que las expresiones de los trozos son continuas en sus intervalos de definición, por lo que tienes que estudiar la continuidad en los puntos de corte: x₁ = -1 y x₂ = 3, por medio de la definición.

Para x₁ = -1:

1°)

f(-1) = (-1)² + a(-1) = 1 - a (1);

2°)

Límites laterales:

Lím(x→-1-) f(x) = Lím(x→-1-) (x² + ax) = (-1)² + a(-1) = 1 - a,

Lím(x→-1+) f(x) = Lím(x→-1+) (b) = b,

y como los límites laterales deben coincidir para que el límite de la función en este punto de corte exista, tienes la ecuación:

b = 1 - a, aquí restas b y sumas a en ambos miembros, y queda:

a = 1 - b (2);

3°)

El valor del límite (que aún debemos determinar) debe ser igual al valor de la función (que aún debemos determinar).

Para x₂ = 3:

1°)

f(3) =2(3) - 4 = 6 - 4 = 2;

2°)

Límites laterales:

Lím(x→3-) f(x) = Lím(x→3-) (b) = b,

Lím(x→3+) f(x) = Lím(x→3+) (2x - 4) = 2(3) - 4 = 6 - 4 = 2,

y como los límites laterales de la función en este punto de corte deben coincider , tienes la ecuación:

b = 2;

3°)

Observa que el valor del límite y el valor de la función para este punto de corte son iguales a 2, por lo tanto tienes que la función es continua en este punto de corte.

Luego, reemplazas el valor remarcado en las ecuaciones señaladas (1) (2), y queda:

f(-1) = 1 - 2 = -1,

a = 1 - 2 = -1;

y observa que el límite de la función para el primer punto de corte es igual a 2.

Luego, la expresión de la función queda:

f(x) = 

x² - x                     si x ≤ -1,

2                            si -1 < x < 3,

2x - 4                     si x ≥ 3;

y observa que la función es continua en el conjunto de los números reales.

Espero haberte ayudado.

Tienes una ecuación cartesiana implícita de una recta:

x - 2y + 4 = 0;

luego, a fin de determinar su intersección con el eje OX, cuya ecuación cartesiana es y = 0, reemplazas el valor remarcado, cancelas el término nulo, y queda:

x + 4 = 0, restas 4 en ambos miembros de esta ecuación, y queda:

x = -4, por lo que tienes que el punto de intersección de esta recta con el eje coordenado OX es:

A(-4,0);

luego, a fin de determinar su intersección con el eje OY, cuya ecuación cartesiana es x = 0, reemplazas el valor remarcado, cancelas el término nulo, y queda:

-2y + 4 = 0, restas 4 en ambos miembros de esta ecuación, y queda:

-2y = -4, divides por -2 en ambos miembros, y queda:

y = 2, por lo que tienes que el punto de intersección de esta recta con el eje coordenado OY es:

B(0,2).

Luego, haz un gráfico cartesiano, y verás que la recta y los ejes coordenados determinan un triángulo rectángulo con vértices en los dos puntos remarcados, y cuyo tercer vértice es el origen de coordenadas.

Luego, planteas las distancias entre cada uno de los puntos remarcados y el origen de coordenadas, y tienes para este triángulo rectángulo:

b = |A0| = 4 (longitud de su cateto base),

h = |0B| = 2 (longitud de su cateto altura);

luego, tienes para el área del triángulo rectángulo:

A_TR = b*h/2 = 4*2/2 = 4.

Espero haberte ayudado.

A)

Tienes las ecuaciones cartesianas paramétricas de la recta r, y observa que un vector director de ella (recuerda que sus componentes son los coeficientes que multiplican al parámetro) es: u_r = < -1 , 2 >.

Luego, plantea la expresión de un vector genérico: U_s = < a , b > (1) que sea perpendicular al vector remarcado, por lo que puedes plantear que el producto escalar entre los dos vectores es igual a cero, y tienes la ecuación vectorial:

u_r • U_s = 0, sustituyes las expresiones de los vectores, y queda:

< -1 , 2 > • < a , b > = 0, desarrollas el producto escalar, y queda:

-a + 2b = 0, restas 2b en ambos miembros, y queda:

-a = -2b, multiplicas en ambos miembros por -1, y queda:

a = 2b (2);

luego, sustituyes en la expresión señalada (2) en la expresión del vector señalada (1), y queda:

U_s = < 2b , b >, extraes el factor escalar b, y queda:

U_s = b*< 2 , 1 >, 

por lo que tienes que cualquier múltiplo no nulo del vector:

u_s = < 2 , 1 > es perpendicular a la recta r.

Luego, con este último vector remarcado, y el punto P(-1,1) que tienes en tu enunciado, planteas las ecuaciones cartesianas paramétricas de una recta perpendicular a la recta r, y queda:

s:

x = -1 + 2p,

y =  1 + p,

con p ∈ R.

Luego, igualas expresiones entre las ecuaciones cartesianas paramétricas de ambas rectas, y queda el sistema de ecuaciones:

2 - t = -1 + 2p (3),

1 + 2t = 1 + p, aquí restas 1 en ambos miembros, y queda: 2t = p (4);

luego, sustituyes la expresión señalada (4) en la ecuación señalada (3), y queda:

2 - t = -1 + 4t, restas 2 y restas 4t en ambos miembros, y queda:

-5t = -3, divides por -5 en ambos miembros, y queda: t = 3/5;

luego, reemplazas el valor remarcado en la ecuación señalada (4), y queda: 6/5 = p;

luego, reemplazas los valores remarcados de los parámetros en sus correspondientes ecuaciones, y tienes para ambos: x = 7/5 e y = 11/5, por lo que tienes que las rectas perpendiculares r y s se cortan en el punto cuya expresión es:

Q(7/5,11/5).

Luego, tienes que la distancia entre el punto P(-1,1) y la recta r es igual a la distancia entre el punto P y el punto Q, por lo que puedes plantear:

d(P,r) = d(P,Q) = √( (7/5+1)²+(11/5-1)² ) = √( (12/5)²+(6/5)² ) = 

= √(144/25+36/25) = √(180/25) = 6√(5)/5.

Espero haberte ayudado.

B)

Sustituyes las expresiones que tienes en las ecuaciones cartesianas paramétricas de la recta r en la ecuación cartesiana implícita de la recta s, y queda:

2(2 - t) - 3(1 + 2t) + 1 = 0, distribuyes, reduces términos semejantes, y queda:

-8t + 2 = 0, restas 2 en ambos miembros, luego divides por -8 en ambos miembros, y queda: t = 1/4;

luego, reemplazas este valor del parámetro en las ecuaciones cartesianas paramétricas de la recta r, y queda: x = 7/4 e y = 3/2, por lo que tienes que el punto de intersección entre las dos rectas es:

T(7/4,3/2).

Espero haberte ayudado.