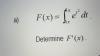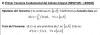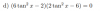Puedes plantear la definición de continuidad para el valor en estudio: x =2 (y observa que el dominio de la función es el conjunto de los números reales):

1°)

f(2) = 3(2) - 5 = 6 - 5 = 1,

por lo que tienes que la función está definida para este valor en estudio;

2°)

Lím(x→2) f(x) = Lím(x→2) (3x - 5) = 3(2) - 5 = 6 - 5 =1,

por lo que tienes que la función tiene límite para el valor en estudio (y observa que la resolución del límite es directa);

3°)

como el valor que toma la función y el límite coinciden para el valor en estudio, puedes concluir que la función es continua en x = 2.

Espero haberte ayudado.

Observa que el dominio de la función es R, y que cada trazo es continuo en su sector del dominio, por lo que solo queda estudiar la continuidad de la función en los puntos de corte (x₁ = 0 y x₂ = 2).

Para x₁ = 0:

1°)

f(0) = 3(0) + 1 = 0 + 1 = 1;

2°)

límites laterales:

Lím(x→0-) f(x) = Lím(x→0-) (3x + 1) = 3(0) + 1 = 0 + 1 = 1,

Lím(x→0+) f(x) = Lím(x→0+) (ax + b) = a(0) + b = 0 + b = b,

y como para que el límite exista tienes que los límites laterales deben coincidir, entonces tienes:

b = 1;

3°)

como el valor de la función y el límite coinciden, tienes que la función es continua en x₁ = 0.

Para x₂ = 2:

1°)

f(2) = 3(2)² - 2 = 3(4) - 2 = 12 - 2 = 10;

2°)

límites laterales:

Lím(x→2-) f(x) = Lím(x→2-) (ax + b) = a(2) + b = 2a + b,

Lím(x→2+) f(x) = Lím(x→2+) (x² - 2) = 4 - 2 = 2,

y como para que el límite exista tienes que los límites laterales deben coincidir, entonces tienes:

2a + b = 2, reemplazas el valor remarcado, y queda:

2a + 1 = 2, restas 1 en ambos miembros, y queda:

2a = 1, divides por 2 en ambos miembros, y queda.

a = 1/2;

3°)

como el valor de la función y el límite coinciden, tienes que la función es continua en x₂ = 2.

Luego, reemplazas los valores remarcados en la expresión de la función que tienes en tu enunciado, y queda:

f(x) =

x² - 2                            si x ≥ 2,

(1/2)x + 1                    si 0 < x < 2,

3x + 1                          si x ≤ 0.

Espero haberte ayudado.

Teorema de la altura y Thales

Observa el triángulo rectángulo sombreado en amarillo:

tienes que la longitud de su altura es la altura de la persona, y que la longitud de su base es la longitud de la sombra de la persona;

luego, planteas la razón entre la longitud de la altura y la longitud de la base, y queda:

r₁ = 1,7/3,4 = 0,5 (1).

Observa el triángulo rectángulo mayor (que incluye al anterior):

tienes que la longitud de su altura es la altura del farol (F), y que la longitud de su base es la suma de la distancia entre el pie del farol y los pies de la persona (4 m) más la longitud de la sombra (3,4 m);

luego, plantea la razón entre la longitud de la altura y la longitud de la base, y queda:

r₂ = F/7,4 (2).

Luego, como los dos triángulos rectángulos son semejantes (revisa en tus apuntes de clase los temas que indica el colega Antonio, y también semejanza de triángulos), tienes que las dos razones son iguales, por lo que puedes plantear:

r₂ = r₁, sustituyes las expresiones señaladas (2) (1), y queda:

F/7,4 = 0,5, multiplicas por 7,4 en ambos miembros, y queda:

F = 3,7 m.

Espero haberte ayudado.

Hola lo de sacar factor común 4 solo es comodidad de trabajar con números de menor valor, daría lo mismo si se hace sin sacar factor común

Hola Jóse,yo veo bien tus resultados,esa serie del último es un ejemplo bastante típico después de ver el teorema de Leibniz,,dice que si 

a1≥a2≥a3....≥0 y que lim an=0 cuando n→oo, entonces la serie 

∑(-1)ⁿ⁺¹ an=a1-a2+a3..... converge

Nota que en efecto la serie que tienes cumple con las hipotésis, y además,es una serie que converge condicionalmente,pues ∑ 1/n no converge,por otro lado,veamos que la suma parcial S2=-1/2 y el mismo teorema en la demostracion te indica que S2≥S (De hecho,como mencionas,converge a -ln2) la contradicción se da porque se da por supuesto que las operaciones váildas en sumas finitas conservan su válidez en sumas infinitas,normalmente así se comportan las series que convergen condicionalmente.Como "extra" te menciono que para las series condicionalmente convergentes,siempre podemos encontrar una "reordenacion" de la serie de tal modo que esa "reordenacion" converga a cualquier número.

Te dejo la prueba del teorema de Leibniz,cualquier cosa nos dices

http://www.ma.uva.es/~antonio/Industriales/Apuntes_12-13/Mat1/SucesionesSeries_Anexo.pdf

Muchas gracias Alejandro. Tengo dudas sobre todo en la última parte del ejercicio, que coincide con la última foto que he mandado. ¿Esa solución es correcta (S= -2•Ln2)? No estoy seguro ya que estoy contradiciendo el razonamiento del enunciado (S=0).