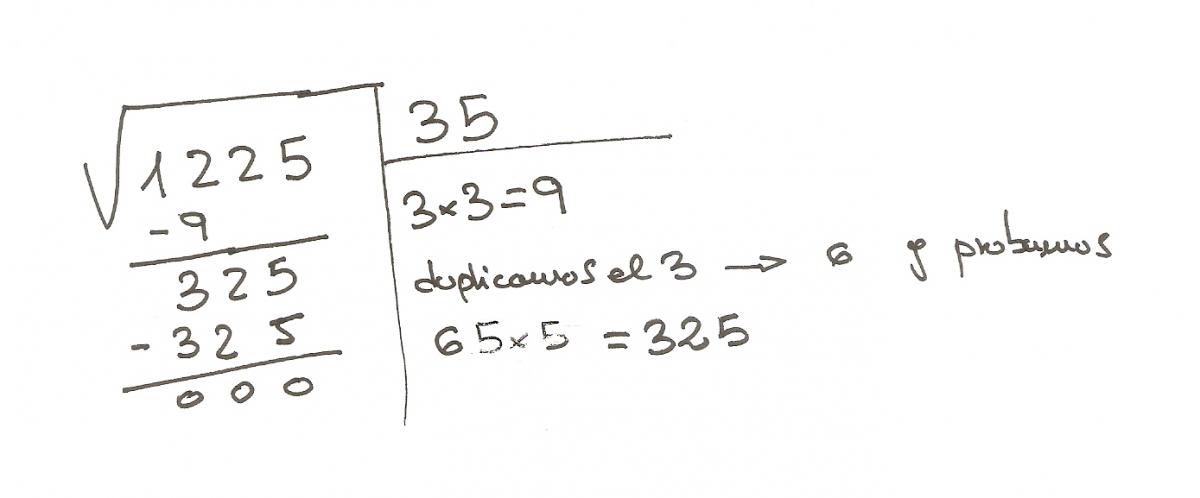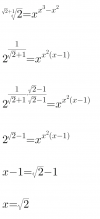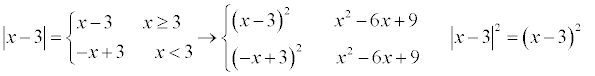-
Paula Sánchez
el 10/8/18 -
Rubén
el 10/8/18-¿La curva que forma la función racional 1/x es una hipérbola?
- Según la teoría, dicha función tiene una asíntota vertical en x = 0 y otra horizontal en y = 0. Pero también según la teoría, las asíntotas jamás cortan a la hipérbola y en esta función cuando y tiende a infinito x = 0 por lo que no se cumple lo anterior. ¿Entonces la curva de dicha función racional qué nombre recibe?
César
el 10/8/18Léete este artículo.
Verás que no es cierto.
https://www.gaussianos.com/calcular-las-asintotas-de-una-funcion/
Rubén
el 10/8/18Rubén
el 11/8/18 -
Gemma Urbano vegas
el 10/8/18 -
JUAN AMPIE
el 10/8/18
Hola muy buenas noches, quería saber si la lógica que usé para resolover la 1ra imágen esta bien por que estoy en duda púes trate de hacer lo mismo para la otra imagen y no es lo mismo.Quisiera saber si tuve suerte y cual sería el procedimiento correcto de antemano muchas gracias
-
Nicolas
el 10/8/18 -
Facu Imfeld
el 10/8/18
Buenas noches, una duda muy puntual respecto a esta inecuación
es válido para eliminar las barras de valor absoluto elevar la expresión al cuadrado?
o sea pasar de |x-3| a (x-3)^2
y de ser así, cuál sería el fundamento teórico que lo justifique? Muchas gracias
-
magui
el 9/8/18
Hola a todos, como resolvería ese ejercicio? Gracias 
Antonio Silvio Palmitano
el 9/8/18Vamos con la primera proposición:
0 < |x + 2| < 1;
observa que es una inecuación doble, de la que tratamos cada una de sus desigualdades por separado:
a)
0 < |x + 2|,
que es Verdadera para todo valor x perteneciente al conjunto de los números reales, excepto el -2 (observa que cero es menor o igual que cualquier valor absoluto, y que para x = -2 es el único valor para el cuál la inecuación es Falsa),
b)
|x + 2| < 1,
aquí observa que el argumento del valor absoluto (revisa tus apuntes de clase) puede tomar valores estrictamente comprendidos entre -1 y 1, por lo que puedes plantear la inecuación doble:
-1 < x + 2 < 1, aquí restas 2 en los tres miembros de la inecuación doble, y queda:
-3 < x < -1;
luego, observa que el conjunto de verdad de la primera proposición queda expresado:
D1 = (-3,-2) ∪ (-2,-1).
Vamos con la segunda proposición:
x = 0,
cuyo conjunto de verdad queda expresado:
D2 = {0}.
Luego, observa que la condición que cumplen los elementos del conjunto está expresada como una disyunción (∨), por lo que puedes plantear que es igual a la unión de los dos conjuntos de verdad (recuerda la definición de unión de conjuntos), y queda:
D = D1 ∪ D2, sustituyes expresiones, y queda:
D = (-3,-2) ∪ (-2,-1) ∪ {0}.
Espero haberte ayudado.
magui
el 11/8/18
Antonio Silvio Palmitano
el 12/8/18Observa que en la definición del conjunto tienes una disyunción, por lo que sus elementos pueden pertenecer a los conjuntos de verdad de una de las proposiciones solamente, o a ambas a la vez.
Observa que el cero pertenece al conjunto de verdad de la segunda proposición, pero no pertenece al conjunto de verdad de la primera.
Espero haberte ayudado.
-
Ana Castillo
el 9/8/18 -
José Luis
el 9/8/18Hola, Por favor alguien me podría ayudar a calcular la parametrización de la curva intersección de éstas dos superficies : x + y^2 - 5y = 0 , -2x -y^3 + z -1=0. Por favor, lo necesito para hacer un problema y estoy atascado en esta parte. Saludos y Gracias.
Antonio Silvio Palmitano
el 9/8/18Puedes despejar x en la primera ecuación, y queda:
x = -y2 + 5y (1);
luego, sustituyes la expresión señalada (1) en la segunda ecuación, y queda
-2(-y2 + 5y) - y3 + z - 1 = 0, distribuyes el primer término, despejas z, y queda:
z = y3 - 2y2 + 10y + 1 (2).
Luego, puedes asignar el parámetro a la variable y, sustituyes en las ecuaciones señaladas (1) (2), y queda el sistema de ecuaciones cartesianas paramétricas de la curva:
x = -t2 + 5t,
y = t,
z = t3 - 2t2 + 10t + 1,
t ∈ R;
y observa que el sentido de recorrido de la curva es acorde al sentido positivo del eje OY.
Espero haberte ayudado.
-
Diego Mauricio Heredia
el 9/8/18
