-
Raúl RC
el 4/3/19Andrea lamento no poder ayudarte pero no resolvemos dudas universitarias que no tengan que ver específicamente con los vídeos ya grabados por el profe, lo lamento de corazón.
Ójala algún otro unico universitario pueda ayudarte, de hecho la idea sería que os ayudarais los unos a los otros.
Usuario eliminado
el 4/3/19Es que yo voy muy mal en Física, y estoy tratando de pasar y me e esforzado bastante e durado bastantes horas tratando de resolver problemas y no e podido. Y precisamente porque no esta la explicación en los videos del profesor por eso pregunte. Si no necesitara ayuda urgentemente no estaria preguntando.
-
Hola me podeís ayudar con este problema:
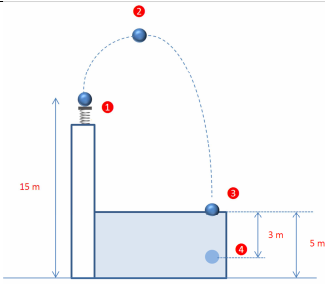
Un cuerpo, de 1 kg de masa, está situado en un trampolín
de 15 m de altura. El cuerpo será impulsado mediante un muelle, de
k=4.000 N/m, que se ha comprimido 10 cm. En su caída, el cuerpo
encontrará un baño con aceite, de 5 m de altura, en el que penetrará
3m. Determinar:
a) La altura máxima alcanzada por el cuerpo (Punto 2).
b) La velocidad con la que llega al aceite (Punto 3).
c) La fuerza de rozamiento ejercida por el aceite.Sobre todo el punto c) me genera muchas dudas
Antonio Silvio Palmitano
el 4/3/19Puedes plantear conservación de la energía entre el instante en que el cuerpo está en reposo con el muelle comprimido y el instante en que el cuerpo se está moviendo con el muelle relajado (consideramos un sistema de referencia con origen a nivel del suelo en la vertical del trampolín, con eje OX horizontal con sentido positivo hacia la derecha, y con eje OY vertical con sentido positivo hacia arriba):
(1/2)*k*Δs2 + M*g*h0 = (1/2)*M*v12 + M*g*h1,
reemplazas datos (k = 4000 N/m, M = 1 Kg, g = 10 m/s2, Δs = 10 cm = 0,1 m, h0 = 15 -0,1 = 14,9 m, h1 = 15 m), y queda:
(1/2)*4000*0,12 + 1*10*14,9 = (1/2)*1*v12 + 1*10*15,
resuelves términos, y queda:
20 + 149 = (1/2)*v12 + 150,
y de aquí despejas:
v1 = √(38) ≅ 11,747 m/s, que es el valor de la rapidez del cuerpo al desprenderse del muelle.
Luego, planteas las expresiones de la posición y de la rapidez para la componente vertical de Tiro Oblicuo (o Parabólico, observa que consideramos el instante inicial: ti = 0 correspondiente al momento en que el cuerpo se desprende del muelle, y observa que no tienes datos que permitan plantear el desplazamiento horizontal del cuerpo), y queda:
y = y1 + v1*t - (1/2)*g*t2,
vy = v1 - g*t,
reemplazas datos, y queda:
y ≅ 15 + 11,747*t - 5*t2 (1),
vy ≅ 11,747 - 10*t (2).
a)
Planteas la condición de altura máxima (el cuerpo "no sube ni baja" en ese instante), y queda:
vy = 0, sustituyes la expresión señalada (2), y queda:
11,747 - 10*t ≅ 0, y de aquí despejas:
t ≅ 1,175 s, que es el valor del instante correspondiente;
luego, reemplazas este valor en la ecuación señalada (1), resuelves, y queda:
yM ≅ 21,900 m, que es el valor de la altura máxima que alcanza el cuerpo.
b)
Planteas la condición de llegada del cuerpo al nivel de la superficie de aceite, y queda:
y = 5 m, sustituyes la expresión señalada (1), y queda:
15 + 11,747*t - 5*t2 ≅ 5, restas 5 en ambos miembros, y queda:
10 + 11,747*t - 5*t2 ≅ 0, divides por -5 en todos los términos, ordenas términos, y queda:
t2 - 2,349*t - 2 ≅ 0, que es una ecuación polinómica cuadrática cuyas soluciones son:
b1)
t ≅ (2,349-3,677)/2 ≅ -0,664 s, que no tiene sentido para este problema;
b2)
t ≅ (2,349+3,677)/2 ≅ 3,008 s, que sí tiene sentido para este problema;
luego, reemplazas este valor en la ecuación señalada (2), y queda:
vy3 ≅ 11,747 - 10*3,008, resuelves, y queda:
vy3 ≅ -18,333 m/s, que es el valor de la velocidad del cuerpo justo antes de tocar el aceite.
c)
Planteas la ecuación trabajo-energía para el trayecto del cuerpo dentro del aceite (observa que consideramos que el cuerpo se desplaza con dirección vertical), y queda:
Wfr = EM4 - EM3, sustituyes expresiones, y queda:
Wfr = M*g*y4 - (M*g*y3 + (1/2)*M*vy32), reemplazas valores, y queda:
Wfr ≅ 1*10*(5-3) - (1*10*5 + (1/2)*1*(-18,333)2), resuelves términos, y queda:
Wfr ≅ 20 - (50 + 168,049), resuelves el agrupamiento, y queda:
Wfr ≅ 20 - 218,049, resuelves, y queda:
Wfr ≅ -198,049 J;
luego, sustituyes la expresión del trabajo realizado por la fuerza de rozamiento promedio (recuerda que esta fuerza es disipativa, por lo que su trabajo es negativo), y queda:
-fr*Δy ≅ -198,049, reemplazas el valor del módulo del desplazamiento del cuerpo (Δy = 3 m), y queda:
-fr*3 ≅ -198,049, divides por -3 en ambos miembros, y queda:
fr ≅ 66,026 N, que es el valor promedio del módulo de la fuerza de rozamiento que ejerce el aceite sobre el cuerpo.
Espero haberte ayudado.
-
Por favor me podéis ayudar con este ejercicio:
Es una lente DIVERGENTE que forma una imagen virtual y derecha de un objeto situado 10cm delante de ella. Si el aumento lateral es 0,4. Me piden:
1) el diagrama de rayos
2) la distancia focal de la lente.
Gracias
-
Alguien me podria ayudar con este problema?
Esta en catalan pero creo que se entiende bien. Se que el campo de las dos cargas que estan en el eje y (x=0) se anulan pero nose como encontrar el valor de las dos otras cargas las cuales nos dan las coordenadas. Gracias
Raúl RC
el 4/3/19Debes aplicar el principio de superposición tal y como el profe ha hecho en este vídeo, el problema es que en tu ejercicio empiezas por el final, pero el fundamento es exactamente el mismo, nos cuentas ;)
https://www.youtube.com/watch?v=Obh1NVyz_No&list=PLOa7j0qx0jgMEZgKsardkZGh38EUj-kfc&index=2
-
Me podrían decir cómo resolver esos dos? Yo me encargo de hacer los cálculos pero es que no sé cómo plantearlos

Bravo
el 3/3/19Bravo
el 3/3/19Para el número 5 te propongo el siguiente planteamiento:
El resorte se ha alargado de 4 in (desde 12 in a 16 in) ¿cierto? Por lo tanto, podemos calcular la tensión de la cuerda, que será la misma que hace el resorte sobre la cuerda. T = 4x4= 16lb.
Sabiendo la tensión de la cuerda podemos ir al esquema de las fuerzas que actúan sobre el collarín y calcular el peso.
P= peso del collarín
θ= ángulo que forma la cuerda con la vertical
Podemos descomponer la tensión:
T.cosθ = P
Para el ángulo θ y en base a las medidas del dibujo, sacamos la tangente (12/16 = 3/4).
Sabiendo el valor de la tangente ya puedes calcular las demás razones trigonométricas que hagan falta.
Espero haber sido de ayuda, un saludo.
-
Buenos dias me gustaria saber si estan bien. Dos cargas eléctricas puntuales de valores q1 = -10 µC y q2 = 5 µC están situadas en los puntos (-1,0) y (0,0) respectivamente del plano XY.
Coordenadas expresadas en metros)
Determine el campo electrostático E (módulo, dirección y sentido) en el punto P de coordenadas (1,0). Me da direccion: (-67500 i , 0 j). Modulo: 67500 N/C
Calcule el valor del potencial electrostático en dicho punto P. Y esto me da que es 0 voltios
Gracias un saludo
Antonio Silvio Palmitano
el 3/3/19Para la primera carga tienes:
q1 = -10*10-6 C, ubicada en el punto: A(-1,0),
y el vector dirección queda: u1 = AP = < 2 , 0 >, cuyo módulo es: │u1│ = 2 m,
y el vector unitario correspondiente queda: U1 = < 1 , 0 >;
luego, la expresión vectorial del campo eléctrico producido por esta carga en el punto P queda:
E1 = (k*q1/│u1│2)*U1, reemplazas expresiones, y queda:
E1 = (9*109*(-10*10-6)/22)*< 1 , 0 >, resuelves el coeficiente, y queda:
E1 = -22,5*103*< 1 , 0 > N/C;
luego, planteas la expresión del potencial en el punto P, y queda:
V1 = k*q1/│u1│, reemplazas expresiones, y queda:
V1 = 9*109*(-10*10-6)/2, resuelves, y queda:
V1 = -45*103 V.
Para la segunda carga tienes:
q2 = 5*10-6 C, ubicada en el punto: B(0,0),
y el vector dirección queda: u2 = BP = < 1 , 0 >, cuyo módulo es: │u2│ = 1 m,
y el vector unitario correspondiente queda: U2 = < 1 , 0 >;
luego, la expresión vectorial del campo eléctrico producido por esta carga en el punto P queda:
E2 = (k*q2/│u2│2)*U2, reemplazas expresiones, y queda:
E2 = (9*109*(5*10-6)/12)*< 1 , 0 >, resuelves el coeficiente, y queda:
E2 = 45*103*< 1 , 0 > N/C;
luego, planteas la expresión del potencial en el punto P, y queda:
V2 = k*q2/│u2│, reemplazas expresiones, y queda:
V2 = 9*109*(5*10-6)/1, resuelves, y queda:
V1 = 45*103 V.
Luego, planteas la expresión vectorial del campo eléctrico resultante en el punto P, y queda:
E = E1 + E2, reemplazas las expresiones de los campos, y queda:
E = -22,5*103*< 1 , 0 > + 45*103*< 1 , 0 >, resuelves, y queda:
E = 22,5*103*< 1 , 0 > N/C.
Luego, planteas la expresión del potencial total en el punto P, y queda:
V = V1 + V2, reemplazas valores, y queda:
V = -45*103 + 45*103, resuelves, y queda:
V = 0 V.
Espero haberte ayudado.
-
Hola buenas, estoy en la universidad en facultad de ingenieria y realmente voy muy mal porque el profesor no explica ni da formulas ni nada. Y realmente espero que ustedes me puedan ayudar. Ya que estoy muy preocupada.
Me podrian ayudar con el problema 12.70 y 12.71 es que no tengo la formula ni como resolverlo.
Movimiento curvilineo
Antonio Silvio Palmitano
el 3/3/1970)
Vamos con una orientación.
Considera un sistema de referencia con origen de coordenadas en el punto de disparo, con eje OX horizontal con sentido positivo hacia la derecha, y con eje OY vertical con sentido positivo hacia arriba, según la figura correspondiente, y con instante inicial: ti = 0 correspondiente al momento del disparo del proyectil.
Luego, planteas las ecuaciones de posición de Tiro Oblicuo (o Parabólico), y quedan:
x = v0*cosθ*t,
y = v0*senθ*t - (1/2)*g*t2,
aquí reemplazas datos que tienes en tu enunciado (observa que consideramos que el módulo de la aceleración gravitatoria terrestre es: g = 32 pies/s2), y queda:
x = 70*cos(65º)*t,
y = 70*sen(65º)*t - 16*t2;
luego, sustituyes las coordenadas del punto de impacto: x = 60 pies, y = h, en las ecuaciones anteriores, y queda:
60 = 70*cos(65º)*t,
h = 70*sen(65º)*t - 16*t2;
y solo queda que despejes el valor del instante de impacto en la primera ecuación, para luego reemplazarlo en la segunda, para luego resolver y determinar la ordenada (altura) del punto de impacto.
Espero haberte ayudado.
Antonio Silvio Palmitano
el 3/3/1971)
70)
Vamos con una orientación.
Considera un sistema de referencia con origen de coordenadas en el punto de disparo, con eje OX horizontal con sentido positivo hacia la derecha, y con eje OY vertical con sentido positivo hacia arriba, según la figura correspondiente, y con instante inicial: ti = 0 correspondiente al momento del disparo del proyectil.
Luego, planteas las ecuaciones de posición de Tiro Oblicuo (o Parabólico), y quedan:
x = v0*cosθ*t,
y = v0*senθ*t - (1/2)*g*t2,
aquí reemplazas datos que tienes en tu enunciado (observa que consideramos que el módulo de la aceleración gravitatoria terrestre es: g = 32 pies/s2), y queda:
x = 80*cosθ*t, de aquí despejas: x/(80*cosθ) = t (1),
y = 80*senθ*t - 16*t2;
luego, sustituyes la expresión señalada (1) en la segunda ecuación, resuelves coeficientes, aplicas la identidad trigonométrica de la tangente en el primer término de la expresión, y queda:
y = x*tanθ - (1/400)*(x2/cos2θ);
luego, sustituyes las coordenadas del punto de impacto: x = 60 pies, y = h, y queda:
h = 60*tanθ - (1/400)*(602/cos2θ),
resuelves el coeficiente en el segundo término de la expresión, y queda:
h = 60*tanθ - 9/cos2θ (2),
que es la expresión de la ordenada (altura) del punto de impacto en función de la medida del ángulo de disparo del proyectil;
luego, derivas la expresión de la función señalada (2) (observa que debes aplicar la Regla de la Cadena en el segundo término), y queda:
h' = 60*(1/cos2θ) - 9*(-2*(-senθ)/cos3θ),
resuelves en ambos términos de la expresión, y queda:
h' = 60/cos2θ -18*senθ/cos3θ (3);
luego, planteas la condición de valor estacionario (posible máximo o posible mínimo), y queda:
h' = 0, sustituyes la expresión señalada (3), y queda:
60/cos2θ -18*senθ/cos3θ = 0, multiplicas por cos3θ en todos los términos, y queda:
60*cosθ - 18*senθ = 0, restas 60*cosθ en ambos miembros, y queda:
-18*senθ = -60*cosθ, divides por -18 y divides por cosθ en ambos miembros, y queda:
tanθ = 10/3, compones en ambos miembros con la función inversa de la tangente, y queda:
θ ≅ 73,301º, que es el valor estacionario para el ángulo de disparo;
luego, evalúas la expresión de la función señalada (2) para este valor estacionario, para un valor menor que él y para otro valor mayor que él, y tienes:
h(73º) = 60*tan(73º) - 9/cos2(73º) ≅ 90,965 m,
h(73,301º) ≅ 60*tan(72,542º) - 9/cos2(72,542º) ≅ 90,997 m,
h(74º) = 60*tan(74º) - 9/cos2(74º) ≅ 90,786 m,
y tienes verificado que el valor estacionario del ángulo de disparo corresponde a un máximo de la ordenada del punto de impacto.
Espero haberte ayudado.


















 .
. 









