-
tengo 270Julios por cada gramo de Hg y tengo que pasar a KJ/g como hag por favor? gracias
-
Querría saber si tengo bien este problema de energía en el que me pregunta la velocidad al final y cuando lleva 90 metros recorridos .
Gracias por vuestro tiempo!
-
 Yo realice este ejercicio de la siguiente manera: mgH = m(Vc^2)/2 + mgRh
Yo realice este ejercicio de la siguiente manera: mgH = m(Vc^2)/2 + mgRh Siendo Vc la velocidad centrípeta y h = R - Rcos(θ) = R( 1+ cosθ)
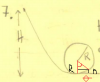
mgH = m(Vc^2)/2 + mgR(1 - cosθ)
2gH - 2gR(1- cosθ) = Vc^2
Ahora hallare todo en función de la normal:
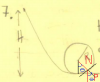 En la direccion hacia dentro del circulo tenemos que: N - mgcosθ =m(Vc^2)/R
En la direccion hacia dentro del circulo tenemos que: N - mgcosθ =m(Vc^2)/RN= mgcosθ + m(2gH - 2gR(1- cosθ))/R =mgcosθ +mg2H/R -mg2R/R + 2mgRcosθ/R = mg (cosθ +2H/R - 2 + 2cosθ)
N = mg( 3cosθ+ 2H/R -2)
Si N=0 ; Vc=0 y θ = 180° (ya que es donde alcanza el máximo el doble del radio del circulo o mejor dicho la maxima altura de la partícula cuando llega a la parte de arriba del circulo)
0= 3cos(180°) -2 +2H/R = -5 + 2H/R => 5R/2 = H
Entonces H tiene que ser H > 5R/2 para dar una vuelta
Ahora para contestar la segunda pregunta si H= 5R/4 (que es la mitad de la altura que se manda a buscar en la primera pregunta) :
Cuando N= 0 y por tanto la partícula empezará a descender del del circulo ya que no tiene fuerza centrípeta que lo mantenga girando y por ende se Vc=0 por un instante:
0= 3cos(θ) -2 +2H/R = 3cos(θ) -2 +(2/R)*(5R/4) = 3cos(θ) -2 +5/2 = 6 cos(θ) -4 + 5
-1/6 = cos(θ)
Ahora se despegara cuando h =R (1- cos(θ)) = R(1+1/6) = R((6+1)/6)= 7R/6
Sin embargo cuando yo lo hago de otra forma no me da el mismo resultado:
Como yo se que Vc = 0 cuando N=0 entonces:
2gH - 2gR(1- cosθ) = Vc^2
2gH - 2gR(1- cosθ) = 0 =2g(5R/4) - 2gR + 2gRcosθ
5/4 - 1 + cosθ = 0
cosθ = -5/4 +1 = (-5 + 4)/4 = -1/4
h =R (1- cos(θ)) = R(1+1/4) = R((4+1)/4)= 5R/4
Como puede ver este h me dio diferente al otro pero deberían ser iguales ¿me podrian decir en que falla mi razonamiento?
Antonio Silvio Palmitano
el 21/2/19a)
Llamamos A al punto inicial de la trayectoria, y llamamos C al punto más alto del rizo.
Observa que en el punto A la altura es H y la velocidad es nula, y observa que en el punto C la altura es 2*R y la velocidad no es nula, ya que el móvil debe tener aceleración centrípeta para mantener el giro, y observa que has consignado correctamente que la acción normal de la pista sobre el móvil es nula en el punto C (el móvil "apenas" se desprende de la pista en este punto).
Luego, planteas conservación de la energía mecánica entre los puntos A y C, y tienes la ecuación:
EMA = EMC, sustituyes expresiones, y queda (observa que la energía cinética en el punto A es igual a cero), y queda:
M*g*H = (1/2)*M*vC2 + M*g*2*R, divides por M en todos los términos, y queda:
g*H = (1/2)*vC2 + 2*g*R (1).
Luego, has aplicado correctamente la Segunda Ley de Newton en el punto C (recuerda que la acción normal de la pista sobre el móvil es nula en este punto, y observa que expresamos a la aceleración centrípeta del móvil en función del módulo de su velocidad tangencial y del radio de la trayectoria circunferencial), y te ha quedado la ecuación:
M*g = M*vC2/R, multiplicas por R y divides por M en ambos miembros, y queda:
g*R = vC2 (2).
Luego, sustituyes la expresión señalada (2) en la ecuación señalada (1), reduces términos semejantes, y queda:
g*H = (5/2)*g*R, divides por g en ambos miembros, y queda:
H = (5/2)*R, que es tu resultado.
b)
Planteas la ecuación de conservación de la energía (observa que indicamos con B al nuevo punto inicial y con D al punto en el cuál el móvil "apenas" se despega de la pista, y observa que en este punto la acción normal de la pista es nula), y queda:
M*g*(5/4)*R = (1/2)*M*vB2 + M*g*HB, multiplicas por 4 y divides por M en todos los términos, y queda:
5*g*R = 2*vB2 + 4*g*HB (3).
Luego, aplicas la Segunda Ley de Newton en el punto B (recuerda que la acción normal de la pista sobre el móvil es nula en este punto, y observa que expresamos a la aceleración centrípeta del móvil en función del módulo de su velocidad tangencial y del radio de la trayectoria circunferencial, y observa además que consideramos positivo el sentido de la dirección radial que va desde el punto B hacia el centro de la trayectoria, y que consideramos que el punto B se encuentra en la parte superior de la misma, por lo que el ángulo θ pertenece al segundo cuadrante, por lo que cosθ es negativo), y queda la ecuación:
-M*g*cosθ = M*vB2/R, multiplicas por R y divides por M en ambos miembros, y queda:
-g*R*cosθ = vB2 (4).
Luego, sustituyes la expresión señalada (4) en la ecuación señalada (3), y queda:
5*g*R = 2*(-g*R*cosθ) + 4*g*HB,
sustituyes la expresión de la altura del punto B en función del ángulo θ y del radio de la trayectoria, y queda:
5*g*R = 2*(-g*R*cosθ) + 4*g*R*(1 - cosθ), divides por g y por R en todos los términos, y queda:
5 = -2*cosθ + 4*(1 - cosθ), distribuyes el último término, y queda:
5 = -2*cosθ + 4 - 4*cosθ, restas 4 en ambos miembros, reduces términos semejantes, y queda:
1 = -6*cosθ, y de aquí despejas:
cosθ = -1/6, aquí compones en ambos miembros con la función inversa del coseno, y queda: θ ≅ 99,594º;
luego, planteas la expresión de la altura del punto B en función del ángulo θ y del radio de la trayectoria, y queda:
HB = R*(1 - cosθ), reemplazas el valor del coseno del ángulo girado por el móvil en la pista circular, resuelves, y queda:
HB = (7/6)*R;
luego, reemplazas el valor del coseno del ángulo girado por el móvil en la pista circular en la ecuación señalada (4), y queda:
-g*R*(-1/6) = vB2, resuelves el primer miembro, y luego despejas:
vB = √(g*R/6),
que es la expresión del módulo de la velocidad del móvil, cuyo valor no es suficiente para obtener el valor del módulo de la aceleración centrípeta necesaria para mantener el giro en el punto B.
Espero haberte ayudado.
-
6. Un niño juega en una terraza i golpea con el dedo una chapa de manera que la tira a una velocidad de 4m/s. El coeficiente de rozamiento es de 0'2.
A Caera la chapa al vacio pasando por la terraza, situada a 3'5m de la chapa cuando esta es golpeada?
Empujamos un cuerpo por una mesa horizontal a una velocidad de 8m/s. El coeficiente de rozamiento entre el cuerpo y la mesa es de 0'7. Contesta:
A Cual es la distancia que recorre el cuerpo antes de detenerse?
B En que se ha convertido ahora el trabajo que ha hecho la fuerza de rozamiento, que a su vez transformó la energia cinetica?
-
HOLA UNICOOS, ME AYUDAIS CON ESTE PROBLEMA? LAS SOLUCIONES QUE ME HA DADO SON ( A= 49000J B=818'67W C=58'3% )
Una bomba de 1400 W de potencia extrae agua de un pozo de 25m de profundidad a razón de 200L/minuto. Calcula
a) El trabajo realizado cada minuto
b) La potencia desarrollada por la bomba
c) El rendimiento de la bomba
Antonio Silvio Palmitano
el 21/2/19Consideramos un eje de posiciones (alturas) OY vertical con sentido positivo hacia arriba y con origen de coordenadas al nivel del suelo.
Tienes los datos:
PotT = 1400 W (potencia total de la bomba),
Q = 200 L/min = 200 Kg/min = 200/60 = 10/3 Kg/s (caudal de agua causado por el bombeo),
yi = -25 m (profundidad del pozo),
yf = 0 (nivel del suelo),
g = 10 m/s2 (módulo de la aceleración gravitatoria terrestre).
a)
Planteas la ecuación Trabajo-Energía, y tienes:
Wb = EPf - EPi, sustituyes las expresiones de las energías, y queda:
Wb = M*g*yf - M*g*yi, reemplazas datos, y queda:
Wb = M*10*0 - M*10*(-25), resuelves términos, cancelas el término nulo, y queda:
Wb = 250*M (1), que es la expresión del trabajo realizado por la bomba (en Joules);
luego, planteas la expresión del la cantidad de agua elevada en función del caudal y del intervalo de tiempo empleado, y queda la ecuación:
M = Q*Δt, reemplazas el valor del caudal y el valor del intervalo de tiempo (Δt = 1 min = 60 s), y queda:
M = (10/3)*60 = 200 Kg, que es el valor de la masa total de agua elevada por la bomba;
luego, reemplazas este último valor en la ecuación señalada (1), resuelves, y queda:
Wb = 50000 J.
b)
Planteas la expresión de la potencia desarrollada por la bomba en función del trabajo realizado y del intervalo de tiempo empleado, y queda:
Potb = Wb/Δt, reemplazas valores, y queda:
Potb = 50000/60 = 2500/3 W ≅ 833,333 W.
c)
Planteas la expresión del rendimiento de la bomba en función de la potencia desarrollada y de la potencia total, y queda:
ε = Potb/PotT, reemplazas valores, y queda:
ε = (2500/3) / 1400, resuelves, y queda:
ε = 25/42 ≅ 0,59524 ≅ 59,524 %.
Espero haberte ayudado.
-
HOLA UNICOOS, ME AYUDAIS CON ESTE PROBLEMA? LAS SOLUCIONES QUE ME HA DADO SON LAS SIGUIENTES:
Un cuerpo de 2 Kg se desplaza por una superficie horizontal debajo de la accion de una fuerza de 10N paralela al plano de deslizamiento. Si el coeficiente de reozamiento es 0'2, calcula:
a) trabajo realizado por la fuerza de arrastre 20J
b) trabajo realizado por la fuerza de rozamiento -7'84J
c) realizarian trabajo la fuerza normal y la fuerza peso? por que? NO
d) cual seria el trabajo total 12'16J
e)si este trabajo se desarrolla en 5s, cual seria la potencia? 2'43W
Antonio Silvio Palmitano
el 22/2/19Tienes los datos:
M = 2 Kg (masa del cuerpo),
F = 10 N (fuerza de arrastre),
μd = 0,2 (coeficiente dinámico de rozamiento),
ti = 0 (instante inicial),
vi = 0 (rapidez inicial del cuerpo),
g = 9,8 m/s2 (módulo de la aceleración gravitatoria terrestre).
Luego, aplicas la Segunda Ley de Newton (consideramos un eje OX horizontal con sentido positivo acorde al desplazamiento del cuerpo, y un eje OY vertical con sentido positivo hacia arriba), y tienes el sistema de ecuaciones:
F - frd = M*a,
N - P = 0,
sustituyes las expresiones del módulo de la fuerza de rozamiento y del módulo del peso del cuerpo, y queda:
F - μd*N = M*a,
N - M*g = 0, de aquí despejas: N = M*g,
luego sustituyes esta última expresión en la primera ecuación, y queda:
F - μd*M*g = M*a, y de aquí despejas:
a = (F - μd*M*g)/M, que es la expresión de la aceleración de cuerpo;
luego, reemplazas datos (consideramos: g = 9,8 m/s2), y queda:
a = (10 - 0,2*2*9,8)/2 = 3,04 m/s2.
Luego, planteas la expresión de la aceleración del cuerpo en función de la variación de su velocidad y del intervalo de tiempo empleado, y queda:
(v - vi)/t = a, multiplicas por t en ambos miembros, y queda:
v - vi = a*t,
reemplazas datos (observa que el valor del instante final lo tienes en el último inciso de tu enunciado), y queda:
v - 0 = 3,04*5, cancelas el término nulo, resuelves el segundo miembro, y queda:
v = 15,2 m/s, que es el valor de la velocidad final del cuerpo.
Luego, planteas la expresión del desplazamiento del cuerpo en función de su velocidad inicial, de su aceleración y del intervalo de tiempo empleado, y queda:
Δx = vi*t + (1/2)*a*t2, reemplazas valores, y queda:
Δx = 0*5 - (1/2)*3,04*52, cancelas el término nulo, resuelves, y queda:
Δx = 38 m.
a)
WF = F*Δx = 10*38 = 380 J.
b)
Wfrd = -frd*Δx = -μd*N*Δx = -μd*M*g*Δx = -0,2*2*9,8*38 = -148,96 J.
c)
Las fuerzas normal (N) y peso (P) son perpendiculares a la dirección de desplazamiento del cuerpo, por lo tanto no realizan trabajo sobre éste.
d)
WT = WF + Wfrd = 380 + (-148,96) = 380 - 148,96 = 231,04 J.
e)
PotT = WT/t = 231,04/5 = 46,208 W.
Espero haberte ayudado.
-
Empujamos un cuerpo por una mesa horizontal a una velocidad de 8m/s. El coeficiente de rozamiento entre el cuerpo y la mesa es de 0'7. Contesta:
BUENAS UNICOOS AYUDARME CON ESTE EJERCICIO PORFAVOR ES URGENTE!! EL PRIMER APARTADO ME HA DADO 4'7m
A Cual es la distancia que recorre el cuerpo antes de detenerse? ( 4'7m )
B En que se ha convertido ahora el trabajo que ha hecho la fuerza de rozamiento, que a su vez transformó la energia cinetica?
Antonio Silvio Palmitano
el 21/2/19Tienes los datos:
vi = 8 m/s (rapidez inicial del cuerpo),
μd = 0,7 (coeficiente dinámico de rozamiento entre la base del cuerpo y la superficie de la mesa),
g = 9,8 m/s2 (módulo de la aceleración gravitatoria terrestre).
A)
Tienes el dato adicional:
vf = 0 (el cuerpo se encuentra en reposo).
Aplicas la Segunda Ley de Newton, y tienes el sistema de ecuaciones (recuerda que la fuerza de rozamiento tiene sentido opuesto al desplazamiento del cuerpo):
-μd*N = M*a,
N - M*g = 0, de aquí despejas: N = M*g (módulo de la acción normal aplicada sobre el cuerpo);
luego, sustituyes esta última expresión en la primera ecuación, y queda:
-μd*M*g = M*a, y de aquí despejas:
a = -μd*g (1) (módulo de la aceleración del cuerpo).
Planteas la ecuación velocidad-desplazamiento de Movimiento Rectilíneo Uniformemente Variado, y queda:
vf2 - vi2 = 2*a*Δx, cancelas el término nulo, sustituyes la expresión señalada (1), y queda:
-vi2 = 2*(-μd*g)*Δx, resuelves signos, despejas, y queda:
Δx = vi2/(2*μd*g) (desplazamiento del móvil),
aquí reemplazas valores, y queda:
Δx = 82/(2*0,7*9,8) = 64/13,72, resuelves, y queda:
Δx ≅ 4,665 m.
B)
Planteas la ecuación Trabajo-Energía Mecánica (observa que la energía potencial gravitatoria permanece constante), y queda:
Wfr = ECf - ECi,
y tienes que el trabajo de la fuerza de rozamiento es igual al valor de la disminución de la energía cinética de traslación del cuerpo, y como esta fuerza es disipativa, tienes que el valor de la disminución de energía pasa al ambiente en forma de calor.
Espero haberte ayudado.
-
BUENAS NOCHES UNICOOS, EN ESTE PROBLEMA CREO QUE ME FALTAN DATOS, DICE ASI:
Un cuerpo de 2okg se mueve a 2m/s por una superficie horizontal y recorre 10m hasta que se detiene. Calcula el trabajo de la fuerza de rozamiento y el coeficiente de rozamiento
Antonio Silvio Palmitano
el 20/2/19Considera un sistema de referencia con eje de posiciones OX horizontal con sentido positivo acorde al desplazamiento del cuerpo, y con eje OY vertical con sentido positivo hacia arriba. Luego, tienes los datos:
M = 20 Kg (masa del cuerpo),
vi = 2 m/s (rapidez inicial del cuerpo),
Δx = 10 m (desplazamiento del cuerpo),
vf = 0 (velocidad final del cuerpo,
g = 10 m/s2 (módulo de la aceleración gravitatoria terrestre).
Luego, planteas la ecuación velocidad-desplazamiento de Movimiento Rectilíneo Uniformemente Variado, y queda:
2*a*Δx = vf2 - vi2, reemplazas valores, cancelas el término nulo, y queda:
2*a*10 = -22, aquí resuelves ambos miembros, y luego despejas:
a = -0,2 m/s2, que es el valor de la aceleración del cuerpo.
Luego, observa que sobre el cuerpo actúan tres fuerzas, de las que indicamos sus módulos, direcciones y sentidos:
Peso: P = M*g = 20*10 = 200 N, vertical hacia abajo,
Acción normal del suelo: N, vertical hacia arriba,
Rozamiento dinámico del suelo: fr = μd*N, horizontal opuesta al desplazamiento del cuerpo;
luego, aplicas la Segunda Ley de Newton, y tienes el sistema de ecuaciones:
-fr = M*a,
N - P = 0;
luego, reemplazas valores en ambas ecuaciones, y queda:
-μd*N = 20*(-0,2), aquí resuelves el segundo miembro, resuelves signos, y queda: μd*N = 4 (1),
N - 200 = 0, de aquí despejas: N = 200 N, que es el módulo de la acción normal del suelo;
luego, reemplazas este último valor remarcado en la ecuación señalada (1), y queda:
μd*200 = 4, de aquí despejas:
μd = 0,02, que es el coeficiente dinámico de rozamiento;
luego, reemplazas los dos últimos valores remarcados en la expresión del módulo de la fuerza de rozamiento, y queda:
fr = 0,02*200, aquí resuelves, y queda: fr = 4 N.
Luego, planteas la ecuación trabajo-energía mecánica (en realidad, observa que solo consideramos la energía cinética de traslación, ya que la energía potencial gravitatoria permanece constante), y tienes la ecuación:
Wfr = ECf - ECi, aquí sustituyes las expresiones de las energías, y queda:
Wfr = (1/2)*M*vf2 - (1/2)*M*vi2, reemplazas valores, y queda:
Wfr = (1/2)*20*02 - (1/2)*20*22, resuelves términos, cancelas el término nulo, y queda:
Wfr = -40 J, que es el valor del trabajo de la fuerza de rozamiento;
y observa que también podrías haberlo calculado por medio de la definición de trabajo (observa que el sentido de la fuerza de rozamiento es opuesto al sentido del desplazamiento del cuerpo):
Wfr = -fr*Δx, reemplazas los valores de los módulos de la fuerza de rozamiento y del desplazamiento, y queda:
Wfr = -4*10, resuelves, y queda:
Wfr = -40 J.
Espero haberte ayudado.






























