-
Me gustaría saber si está bien resuelto ese ejercicio, es el 1. De los dos semáforos del lado izquierdo el enunciado, del lado derecho lo que hice.

Antonio Silvio Palmitano
el 3/3/19Por favor, envía una foto más nítida del enunciado de tu problema para que podamos ayudarte.
De todas maneras, vamos con una orientación.
Observa que designamos con α1, α2 y α3 a los ángulos de inclinación de los tramos de cable con respecto a la horizontal.
Observa que sobre el semáforo ubicado en B actúan tres fuerzas:
Peso, vertical hacia abajo,
Tensión 1, inclinada hacia la izquierda y hacia arriba (hacia el punto A),
Tensión 2, inclinada hacia la derecha y hacia arriba (hacia el punto C);
luego, planteas un sistema de referencia cartesiano usual, y tienes el sistema de ecuaciones:
T1*senα1 + T2*senα2 - PB = 0 (1),
-T1*cosα1 + T2*cosα2 = 0 (2).
Observa que sobre el semáforo ubicado en C actúan tres fuerzas:
Peso, vertical hacia abajo,
Tensión 2, inclinada hacia la izquierda y hacia abajo (hacia el punto B),
Tensión 3, inclinada hacia la derecha y hacia arriba (hacia el punto D);
luego, planteas un sistema de referencia cartesiano usual, y tienes el sistema de ecuaciones:
-T2*senα2 + T3*senα3 - PC = 0 (3),
-T2*cosα2 + T3*cosα3 = 0 (4).
Luego, observa que con las ecuaciones señaladas (1) (2) (3) (4) tienes un sistema de cuatro ecuaciones con cuatro incógnitas (T1, T2, T3 y PC), y observa que con las longitudes que tienes indicadas en la imagen (que son las que no se distinguen con claridad en la imagen) puedes determinar los valores de los senos y de los cosenos de los ángulos.
Espero haberte ayudado.
-
Me dicen que una lente convergente forma de un objeto real una imagen real aumentada dos veces. Al desplazar el objeto 20 cm hacia la lente, la imagen que se obtiene es virtual y con el mismo aumento en valor absoluto. Me piden:
a) La potencia y la distancia focal de la lente
b) realizar el diagrama de rayos.
gracias
Antonio Silvio Palmitano
el 3/3/19Considera un sistema de referencia con origen de coordenadas en el centro óptico de la lente, con eje OX perpendicular al plano de la lente, con sentido positivo hacia la posición inicial del objeto luminoso real, y con eje OY paralelo a la lente.
Luego, tienes las ecuaciones de posición y de aumento, correspondientes a este sistema:
1/x' - 1/x = -1/f (1),
y'/y = m (2),
x'/x = m (3),
f > 0 (observa que la lente es convergente).
Luego, tienes para la primera situación:
m = -2,
x' < 0 (observa que la imagen es real),
y' < 0 (observa que la imagen es invertida debido a que la lente es convergente);
luego, reemplazas el valor del aumento en la ecuación señalada (3), despejas, y queda: x' = -2x (4);
luego, sustituyes la expresión señalada (4) en la ecuación señalada (1), resuelves el signo en el primer término, y queda:
-1/(2x) - 1/x = -1/f, reduces términos semejantes, y queda:
-3/(2x) = -1/f, y de aquí despejas: x = 3f/2 (5).
Luego, tienes para la segunda situación:
X = x - 20 (6) (observa que el objeto se encuentra más cerca de la lente),
m = 2,
x' > 0 (observa que la imagen es real),
y' > 0 (observa que la imagen es derecha debido a que la lente es convergente);
luego, sustituyes la expresión señalada (6) en las ecuación señalada (1), reemplazas el valor del aumento en las ecuación señalada (3), y queda:
1/X' - 1/(x-20) = -1/f (7),
X'/(x-20) = 2, de aquí despejas: X' = 2(x-20), distribuyes y queda: X' = 2x-20 (8);
luego, sustituyes la expresión señalada (5) en la ecuación señalada (8), y queda: X' = 3f-20 (9);
luego, sustituyes las expresiones señaladas (5) (9) en la ecuación señalada (7), y queda:
1/(3f-20) - 1/(3f/2-20) = -1/f, aquí multiplicas por f, por (3f-20) y por (3f/2-20) en todos los términos, y queda:
f*(3f/2-20) - f*(3f-20) = -(3f-20)*(3f/2-20), distribuyes en todos los términos, y queda:
3f2/2 - 20f - 3f2 + 20f = -9f2/2 + 60f + 30f - 400, reduces términos semejantes en ambos miembros, y queda:
-3f2/2 = -9f2/2 + 90f - 400, sumas 9f2/2, restas 90f y sumas 400 en ambos miembros, y queda:
3f2 - 90f + 400 = 0, que es una ecuación polinómica cuadrática, por lo que tienes dos opciones:
1º)
f = ( 90-√(3300) )/6 ≅ 5,426 cm ≅ 0,05426 m, que corresponde a la potencia: P = 1/f ≅ 1/0,05426 ≅ 18,431 dp (dioptrías),
reemplazas el valor de la distancia focal objeto en la ecuación señalada (5), y queda: x ≅ 8,139 cm,
reemplazas este último valor en la ecuación señalada (6), y queda: X ≅ 8,139 - 20 ≅ -11,861 cm,
que no corresponde a la posición de un objeto luminoso real para la segunda situación que tienes en tu enunciado,
por lo que esta opción no tiene sentido para este problema;
2º)
f = ( 90+√(3300) )/6 ≅ 24,574 cm ≅ 0,24574 m, que corresponde a la potencia: P = 1/f ≅ 1/0,24574 ≅ 4,069 dp (dioptrías),
reemplazas el valor de la distancia focal objeto en la ecuación señalada (5), y queda: x ≅ 36,861 cm,
reemplazas este último valor en la ecuación señalada (6), y queda: X ≅ 36,861 - 20 ≅ 16,861 cm,
que sí corresponde a la posición de un objeto luminoso real para la segunda situación que tienes en tu enunciado,
por lo que esta opción sí tiene sentido para este problema, y tienes remarcadas las respuestas del inciso (a).
Queda que hagas el diagrama de la "marcha de rayos" para las dos situaciones que tienes en tu enunciado.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 3/3/19Si estableces un sistema de referencia con origen de coordenadas en el centro óptico de la lente, con eje OX perpendicular a ella con sentido positivo hacia el objeto luminoso real, y con eje OY paralelo a la lente y al objeto luminoso, entonces tienes los siguientes datos:
x = 30 cm (posición del objeto luminoso),
y = 8 cm (altura del objeto luminoso),
f = -15 cm (posición del foco objeto de la lente divergente),
f ' = 15 cm (posición del foco imagen de la lente divergente),
x' = a determinar (posición de la imagen),
y' = a determinar (altura de la imagen con su orientación),
m = a determinar (aumento).
Luego, para este sistema de referencia, tienes las ecuaciones:
1/x' - 1/x = -1/f,
x'/x = m,
y'/y = m;
reemplazas valores, y queda:
1/x' - 1/30 = -1/(-15), de aquí despejas: 1/x'= 1/10, y luego despejas: x' = 10 cm,
x'/30 = m, aquí reemplazas el valor remarcado, resuelves, y queda: 1/3 = m,
y'/8 = m, aquí reemplazas el segundo valor remarcado, despejas, y queda: y' = 8/3 cm ≅ 2,67 cm.
Luego, como la posición de la imagen es positiva, tienes que ésta se encuentra en el campo real,
y como el aumento es positivo, tienes que la imagen es derecha,
y como su valor absoluto es menor que uno, tiene que la imagen es de menor tamaño que el objeto luminoso.
Espero haberte ayudado.
-
Un haz de luz está formado por dos rayos de longitudes de onda λ1 = 400 nm y λ2 = 700 nm respectivamente. Este haz incide, desde el aire, sobre una superficie plana de vidrio con un ángulo de incidencia de 30º.
Determine la velocidad de propagación de cada rayo en el vidrio y el ángulo que forman entre sí los dos rayos refractados.
Datos: Índices de refracción del vidrio: n(λ1 = 400 nm) = 1,66 ; n(λ2 = 700 nm) = 1,61; c = 3,00 × 108 m/s; 1 nm = 10-9 m
Antonio Silvio Palmitano
el 2/3/19Para el primer rayo, tienes los datos:
nv = 1,66 (índice de refracción del vidrio),
na = 1 (índice de refracción del aire),
θa = 30° (ángulo de incidencia),
θv = a determinar (ángulo de emergencia).
Luego, planteas la Ley de Snell y Descartes, y tienes la ecuación:
nv*sen(θv) = na*sen(30°), reemplazas valores, y queda:
1,66*sen(θv) = 1*0,5, divides en ambos miembros por 1,66, resuelves, y queda:
sen(θv) ≅ 0,301, compones en ambos miembros con la función inversa del seno, y queda:
θv ≅ 17,530°.
Luego, planteas la relación entre la rapidez de la luz y los índices de refracción, y queda:
nv*cv = na*c, de aquí despejas:
cv = (na/nv)*c, reemplazas valores, y queda:
cv = (1/1,66)*3*108, resuelves, y queda:
cv ≅ 1,807*108 m/s.
Luego, puedes proceder en forma análoga con los datos que tienes para el segundo rayo.
Espero haberte ayudado.
-
Un protón cruza perpendicularmente un campo magnético de 1'5T y una energía cinética de 5 MeV. ¿De cuánta será la fuerza ejercida sobre él?
Antonio Silvio Palmitano
el 1/3/19Tienes los datos:
B = 1,5 T (intensidad del campo magnético),
K = 5 MeV = 5*106*1,6*10-19 = 8*10-13 J (energía cinética de la partícula),
q = 1,6*10-19 C (carga de la partícula),
M = 1,6726*10-27 Kg (masa de la partícula, tomada de una tabla informativa).
Luego, planteas la expresión de la energía cinética de la partícula, y queda:
(1/2)*M*v2 = K, y de aquí despejas:
v = √(2*K/M) (1).
Luego, planteas la expresión del módulo de la fuerza de origen magnético que actúa sobre la partícula (observa que tienes que la dirección de la fuerza es perpendicular a la dirección de la velocidad), y queda:
|F| = q*v*B*sen(π/2) = q*V*B*1 = q*v*B;
luego, sustituyes la expresión señalada (1), y queda:
|F| = q*√(2*K/M)*B,
que es la expresión del módulo de la fuerza de origen magnético que actúa sobre la partícula, en función de su carga eléctrica (q), de su energía cinética (K), de su masa (M), y del módulo del campo magnético que actúa sobre ella (B).
Luego, solo queda que reemplaces valores y hagas el cálculo.
Espero haberte ayudado.
-
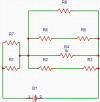
Hola unicoos, soy nuevo en física electrónica. Tengo el siguiente circuito mixto, debo identificar las partes en serie y paralelo. A mi parecer están en serie: R1, R2, R3, R7, R8 y en paralelo: R4, R5, R6.
Pero no estoy seguro si es así. Agradezco mucho vuestra ayuda.
Antonio Silvio Palmitano
el 1/3/19Recuerda que dos resistencias están en serie cuando por ella pasa la misma intensidad de corriente, por lo que tienes que:
R6 y R5 están en serie, y la ecuación para determinar su resistencia equivalente es:
R65 = R6 + R5;
R2 y R3 están en serie, y la ecuación para determinar su resistencia equivalente es:
R23 = R2 + R3.
Recuerda que dos resistencias están en paralelo cuando sus terminales están unidas a un mismo punto, o a puntos que no están separados por otras resistencias, por lo que tienes que:
R7 y R1 están en paralelo, y la ecuación para determinar su resistencia equivalente es:
1/R71 = 1/R7 + 1/R1.
Luego, si sustituyes las asociaciones de resistencias por sus resistencias equivalentes en el circuito, tienes que:
R8, R65, R4 y R23 están en paralelo, y la ecuación para determina su resistencia equivalente es:
1/R865423 = 1/R8 + 1/R65 + 1/R4 + 1/R23.
Luego, si sustituyes esta asociación de resistencias por su resistencia equivalente en el circuito, tienes que:
R71 y R865423 están en serie, y la ecuación para determinar su resistencia equivalente es:
Re = R71 + R865423,
que es la expresión de la resistencia equivalente a todo el circuito.
Espero haberte ayudado.
-
Por favor este problema de lentes me dice:
Una lente delgada forma de un objeto real, situado 40 cm delante de ella, una imagen real e invertida de igual tamaño que el objeto. Me piden:
a) Calcular la posición de la imagen y la potencia de la lente.
b) Realizar la construcción gráfica de la imagen.
Gracias
Antonio Silvio Palmitano
el 28/2/19a)
Establece un sistema de referencia con origen de coordenadas en el centro óptico de la lente delgada, con eje OX perpendicular a la lente con sentido positivo hacia el objeto luminoso real, y con eje OY paralelo a la lente con sentido positivo hacia arriba;
luego, para este sistema de referencia, tienes las ecuaciones (presta atención aquí, porque existen otros sistemas de referencia que se emplean en este tema, que tienen ecuaciones similares pero no idénticas a las que corresponden al que hemos definido aquí):
1/x' - 1/x = -1/f (ecuación de las posiciones),
y '/y = x'/x (ecuación de aumento),
P = 1/f (ecuación de potencia).
Luego, tienes los datos:
x = 40 cm (1) (posición del objeto luminoso),
x' = a determinar (posición de la imagen),
f = a determinar (distancia focal de la lente),
y = a determinar (altura del objeto luminoso, que consideramos es positiva),
y ' = a determinar (altura de la imagen),
y observa que tienes:
x' < 0 porque la imagen es real,
y ' = -y (2), porque la imagen es invertida y de igual tamaño que el objeto.
luego, reemplazas el valor señalada (1) y la expresión señalada (2) en la ecuación de las posiciones y en la ecuación de aumento, y queda el sistema de ecuaciones:
1/x' - 1/40 = -1/f (3),
-y/y = x'/40, aquí simplificas el primer miembro, y luego despejas: x' = -40 cm;
luego, reemplazas el valor remarcado en la ecuación señalada (3), resuelves el primer miembro, y queda:
-1/20 = -1/f, y de aquí despejas: f = 20 cm = 0,2 m;
luego, reemplazas este último valor remarcado en la ecuación de potencia, resuelves, y queda:
P = 5 dp (dioptrías).
Queda que hagas el gráfico correspondiente correspondiente a la "marcha de rayos", haz el intento de hacerlo, y si te resultan necesario no dudes en volver a consultar.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 28/2/19Esta consulta corresponde al Foro de Matemáticas, pero igual ahí vamos.
Puedes comenzar por designar a los cuatro vértices del cuadrado:
A(0,0), B(a,0), C(0,a) y D(a,a);
y luego tienes que la expresión del área del cuadrado en función de las longitudes de sus lados queda:
A = a2 (1).
luego, observa que por simetría, tienes que los triángulos coloreados en rojo y en azul son congruentes, y si consideras que sus bases están sobre los ejes coordenados, tienes que sus alturas, cuyas longitudes designamos H, tienen las mismas medidas.
Luego, planteas las expresiones de las áreas del triángulo azul, y también del triángulo rojo, y queda:
Aa = (1/2)*a*H,
Ar = (1/2)*a*H,
y como tienes que el área del romboide sombreado con negro es igual a las áreas de los dos triángulos coloreados, puedes plantear también que la expresión de su área es:
An = (1/2)*a*H;
luego, planteas la expresión del área del cuadrado como la suma de las áreas de las tres figuras coloreadas, y queda:
A = Aa + Ar + An, sustituyes expresiones, reduces términos semejantes, y queda:
A = (3/2)*a*H (2).
Luego, observa que para los triángulos coloreados en rojo y en azul tienes que uno de sus catetos tiene longitud a, otro de sus catetos tiene longitud H, y la hipotenusa tiene la longitud del radio del cuarto de círculo, por lo que planteas la ecuación pitagórica, y queda:
a2 + H2 = 132, resuelves el segundo miembro, y queda:
a2 + H2 = 169 (3).
Luego, igualas las expresiones del área del cuadrado señaladas (1) (2), y queda la ecuación:
a2 = (3/2)*a*H, aquí multiplicas por 2, divides por 3 y divides por a (observa que a es distinto de cero), y queda:
(2/3)*a = H (4).
Luego, sustituyes la expresión señalada (4) en la ecuación señalada (3), resuelves su segundo término, y queda:
a2 + (4/9)*a2 = 169, reduces términos semejantes, y queda:
(13/9)*a2 = 169, multiplicas por 9 y divides por 13 en ambos miembros, y queda:
a2 = 117 (5).
Luego, reemplazas el valor señalado (5) en la ecuación señalada (1), y queda:
A = 117.
Espero haberte ayudado.
-
Alguien que me pueda ayudar a resolver estos problemas, tengo que plantear las ecuaciones y dar el resultado.
1.-Una lancha de motor requirió una hora más para viajar 60 millas contra la corriente de lo que requirió para avanzar 60 millas con la corriente. La velocidad de la corriente era 1mph. Calcula la velocidad de la lancha en aguas en calma.
2.- Un corredor recorrió 7 millas a una velocidad constante y después la redujo 3 mph. Corrió 8 millas adicionales a la velocidad reducida. El tiempo total que transcurrió corriendo las 15 millas fue 3 horas. Calcula la velocidad de las últimas 8 millas.
Antonio Silvio Palmitano
el 28/2/191)
Llamamos:
v: rapidez de la lancha con respecto al agua en reposo,
vc = 1 M/h: rapidez de la corriente de agua,
v-vc = v-1: rapidez de la lancha cuando se desplaza en contra de la corriente (en M/h),
v+vc = v+1: rapidez de la lancha cuando se desplaza a favor de la corriente (en M/h),
t: tiempo empleado en el trayecto recorrido a favor de la corriente,
t+1: tiempo empleado en el trayecto en contra de la corriente,
L = 60 M: distancia recorrida.
Luego, planteas la expresión de desplazamiento de Movimiento Rectilíneo Uniforme para las dos situaciones, y queda:
(v-1)*(t+1) = 60, aquí distribuyes, y queda: v*t + v - t - 1 = 60, restas 60 en ambos miembros, y queda: v*t + v - t - 61 = 0 (1),
(v+1)*t = 60, de aquí despejas: t = 60/(v+1) (2);
luego, sustituyes la expresión señalada (2) en la ecuación señalada (1), y queda:
v*60/(v+1) + v - 60/(v+1) - 61 = 0, multiplicas por (v+1) en todos los términos, y queda:
60*v + v*(v+1) - 60 - 61*(v+1) = 0, distribuyes agrupamientos, y queda:
60*v + v2 + v - 60 - 61*v - 61 = 0, reduces términos semejantes, ordenas términos, y queda:
v2 - 121 = 0, sumas 121 en ambos miembros, y queda:
v2 = 121, extraes raíz cuadrada positiva en ambos miembros, y queda:
v = 11 M/h;
luego, reemplazas el valor remarcado en la ecuación señalada (2), resuelves, y queda:
t = 5 h.
Espero haberte ayudado.
Antonio Silvio Palmitano
el 28/2/192)
Llamamos:
L1: = 7 M: distancia recorrida en la primera etapa,
v: rapidez del corredor en la primera etapa (en M/h),
t1: tiempo empleado en la primera etapa,
L2: = 8 M: distancia recorrida en la segunda etapa,
v-3: rapidez del corredor en la segunda etapa (en M/h),
t2: tiempo empleado en la segunda etapa,
t = 3 h: tiempo total empleado.
Luego, planteas la ecuación de desplazamiento de Movimiento Rectilíneo Uniforme para las dos etapas, planteas la relación entre los tiempos empleados, y queda el sistema de ecuaciones:
v*t1 = 7, de aquí despejas: t1 = 7/v (1),
(v-3)*t2 = 8, de aquí despejas: t2 = 8/(v-3) (2),
t1 + t2 = 3;
luego, sustituyes las expresiones señaladas (1) (2) en la última ecuación, y queda:
7/v + 8/(v-3) = 3, multiplicas por v*(v-3) en todos los términos, y queda:
7*(v-3) + 8*v = 3*v*(v-3), distribuyes agrupamientos, y queda:
7*v - 21 + 8*v = 3*v2 - 9*v, restas 3*v2 y sumas 9*v en ambos miembros, reduces términos semejantes, ordenas, y queda:
-3*v2 + 24*v - 21 = 0, divides por -3 en todos los términos, y queda:
v2 - 8*v + 7 = 0, que es una ecuación polnómica cuadrática, cuyas soluciones son:
a)
v = 1 M/h, que al reemplazar y resolver en las ecuaciones señaladas (1) (2), queda:
t1 = 7 h,
t2 = -4 h,
y observa que este último valor no tiene sentido para este problema;
b)
v = 7 M/h, que al reemplazar y resolver en las ecuaciones señaladas (1) (2), queda:
t1 = 1 h,
t2 = 2 h,
y observa que todos los valores sí tienen sentido para este problema,
por lo que puedes concluir que la rapidez del corredor en la segunda etapa es: 7-3 = 4 M/h.
Espero haberte ayudado.