-
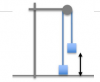
Considerar el sistema de la polea de la figura. Bloque en el suelo tiene una masa de 4 kg. El bloque suspendido a 2 m sobre el suelo tiene una masa de 12 kg. Suponiendo que la polea no tiene masa y no existe fricción entre la polea y la cuerda, se deja el sistema en libertad.
a) ¿Cuál es la velocidad del bloque más pesado justo antes de impactar en suelo?
b) ¿Cuánto tarda en golpear el suelo?
El a) ningún problema pero en el b) no sé como encontrar el tiempo mediante las formulas de Energía y trabajo. Hay que hacer cinemática?
-
Raúl RC
el 10/12/17Hola! Me encantaría ayudarte, pero no respondemos dudas universitarias que no tengan que ver específicamente con los videos que ya ha grabado como excepcion el profe. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Antonio Silvio Palmitano
el 7/12/17Plantea que el empuje resultante es igual a la suma de los empujes (observa que tienen dirección vertical y sentido hacia arriba) que ejercen los líquidos sobre el cuerpo:
E = E1 + E2.
Luego, plantea las expresiones de los módulos de los empujes por separado:
E1 = ρ1*Vs1*g = 800*2*10 = 16000 N = 16 KN;
E2 = ρ2*Vs2*g = 1200*3*10 = 36000 N = 36 KN.
Luego, el módulo del empuje resultante queda:
E = 16 + 36 = 52 KN.
Por favor, consulta con tus docentes porque es probable que haya errores de imprenta en el enunciado.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 7/12/17Observa que el volumen sumergido es igual a la mitad del volumen del cuerpo.
Luego, plantea la expresión del módulo del peso del cuerpo:
P = δc*V*g.
Luego, plantea la expresión del módulo del empuje hidrostático que el líquido ejerce sobre el cuerpo:
Luego, plantea la expresión del módulo del empuje hidrostático que el líquido ejerce sobre el cuerpo:
E = δL*(V/2)*g.
Luego, plantea la condición de equilibrio:
E = P, sustituyes expresiones, y queda:
δL*(V/2)*g = δc*V*g, divides en ambos miembros por V*g, y queda:
δL/2 = δc, que es la relación entre la densidad del cuerpo (a determinar) y la densidad del líquido (agua: 1000 Kg/m3).
Luego, reemplazas en la ecuación remarcada, y tienes:
500 Kg/m3 = δc, que es el valor de la densidad de masa del cuerpo.
Luego, plantea la expresión de la masa del cuerpo:
M = δc*V = reemplazas valores = 500*4 = 2000 Kg.
Luego, plantea la expresión del módulo del empuje hidrostático:
E = δL*(V/2)*g = reemplazas valores = 1000*(4/2)*10 = 20000 N = 20 KN.
Luego, plantea la expresión del módulo de peso del cuerpo:
P = δc*V*g = reemplazas valores = 500*4*10 = 20000 N,
y observa que los módulos del peso y del empuje son iguales, por lo que tienes que el cuerpo se encuentra en equilibrio.
Luego, observa los valores remarcados y tienes que la opción (a) es la respuesta correcta.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 6/12/17Para los cuerpos ubicados en sus posiciones iniciales:
a)
xcm = (M1*x1 + M2*x2)/(M1 + M2) = (500*(-10) + 500*10)/(500+500) = (-5000 + 5000)/1000 = 0/1000 = 0,
ycm = (M1*y1 + M2*y2)/(M1 + M2) = (500*0 + 500*0)/(500+500) = 0/1000 = 0,
por lo que la posición inicial del centro de masas es: R = 0i + 0j = < 0 ; 0 > cm.
b)
xcm = (M1*x1 + M2*x2)/(M1 + M2) = (520*(-10) + 480*10)/(520+480) = (-5200 + 4800)/1000 = -400/1000 = -0,4,
ycm = (M1*y1 + M2*y2)/(M1 + M2) = (500*0 + 500*0)/(500+500) = 0/1000 = 0,
por lo que la posición inicial del centro de masas es: R = -0,4i + 0j = < -0,4 ; 0 > cm.
Para los cuerpos en movimiento:
c)
observa que el cuerpo de la izquierda desciende y que el cuerpo de la derecha asciende;
luego, aplicas la Segunda Ley de Newton en cada cuerpo, y tienes el sistema de ecuaciones (observa que consideramos como positivo al sentido de movimiento en cada cuerpo):
M1*g - T = M1*a
T - M2*g = M2*a,
sumas miembro a miembro (observa que tienes cancelaciones), extraes factores comunes, y queda
(M1 - M2)*g = (M1 + M2)*a, reemplazas valores, y queda (observa que consideramos: g = 1000 cm/s2):
(520 - 480)*1000 = (520 + 480)*a, resuelves coeficientes, y queda:
40000 = 1000*a, haces pasaje de factor como divisor, y queda:
40 = a, por lo que tienes que el módulo de las aceleraciones de los cuerpos es a = 40 cm/s2;
luego, observa que las expresiones vectoriales de las aceleraciones de los cuerpos quedan
a1 = < 0 ; -40 > = 0i - 40j = - 40j,
a2 = < 0 ; 40 > = 0i + 40j = 40j;
luego, plantea la expresión de la aceleración del centro de masa:
acm = (520*(-40) + 480*(40) )/(520+480) = (-20800+19200)/1000 = -1600/1000 = -1,6j cm/s2.
d)
observa que el movimiento es vertical, y que la posición inicial del Centro de Masas es R = -0,4i + 0j;
luego, observa que la posición horizontal permanece constante, y si consideras que la velocidad inicial es nula, plantea la ecuación de velocidad de Movimiento Rectilíneo Uniformemente Variado, plantea para la componente vertical de la velocidad:
vf = vi + acm*t, reemplazas valores, y queda:
vf = 0 - 1,6*2 = -3,2j cm/s2, que es la velocidad en el instante en estudio (t = 2 s);
luego, plantea la ecuación de posición (recuerda que la posición inicial horizontal permanece constante), y queda
xf = -0,4i,
yf = (1/2)*a*t2 = reemplazas valores = (1/2)*(-1,6)*22 = -3,2 cm;
luego, la expresión de la posición final queda:
Rf = -0,4i - 3,2j = < -0,4 ; -3,2 > cm.
Espero haberte ayudado.
-
-
Calcular la densidad en g/cm3 de un cuerpo cuya masa es 471 kg y ocupa 3m3 .
Tema: Hidrostática
Ayuda por favor
Raúl RC
el 6/12/17échale un vistazo a estos vídeos, nos cuentas ;)
https://www.youtube.com/watch?v=ernSMwm3RC4
https://www.youtube.com/watch?v=xyRsmkoMGh8
-
Calcular el peso específico de aire (P aire = 0,0013 g/cm3 ) (g= 10 m/s2 )
Tema : Hidrostática
Ayuda por favor
Antonio Silvio Palmitano
el 6/12/17Tienes el valor de la densidad de masa del aire:
ρai = 0,0013 g/cm3 = 0,0013*1000000/1000 = 1,3 Kg/m3.
Luego, plantea la expresión del peso específico del aire en función de su densidad:
Pai = ρai*g = 1,3 Kg/m3 * 10 m/s2 = (1,3*10) (Kg*m/s2)/m3 = 13 N/m3.
Espero haberte ayudado.