-
Carlos
el 13/10/17
Para una altura h y módulo de la velocidad v0 dados, calcular el ángulo de la plataforma para conseguir el salto
Raúl RC
el 14/10/17Échale un vistazo a los videos de tiro oblicuo
A partir de ahí, se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok?
-
Carlos
el 13/10/17Como podría calcular la velocidad y dirección de un avión respecto a tierra? que ecuaciones debería de plantear? digamos que su velocidad (modulo) y dirección son relativas al aire en el que se mueven i ese aire tiene una dirección y velocidad relativa a la tierra.
-
Mikel Delgado
el 13/10/17Una bola de nieve rueda del techo de un granero con inclinación hacia abajo de 40º. El borde del techo está a 14 m del suelo y la bola tiene una rapidez de 7.00 m/s al salir del techo. Puede despreciarse la resistencia del aire.
a) ¿A qué distancia del borde del granero golpea la bola el piso si no golpea otra cosa al caer?
b) Un hombre de 1.9 m de estatura está parado a 4 m del granero, ¿lo golpeará la bola?
Ayuda por favor, gracias
-
Mikel Delgado
el 13/10/17Es común ver a las aves de presa ascender en corrientes calientes de aire, por lo general, describiendo una trayectoria espiral. Se puede modelar un movimiento espiral como movimiento circular uniforme combinado con una velocidad constante hacia arriba. Suponga que un ave describe un círculo completo con radio 8 m cada 5 s y asciende verticalemente a razón de 3.00 m/s. Determine:
a) La rapidez del ave relativa al suelo
b) la aceleración del ave (magnitud y dirección)
c) El ángulo entre el vector velocidad del ave y la horizontal
No sé ni por donde empezar
Antonio Silvio Palmitano
el 13/10/17Puedes plantear:
ω = 1 giro / 5 s = 2π/5 rad/s (rapidez angular),
u = 3 m/s (rapidez de ascenso).
Luego, puedes plantear la función vectorial de posición
r(t) = < 8*cos( (2π/5)*t ) , 8*sen( (2π/5)*t ) , 3*t >.
Luego, derivas y tienes la expresión de la función vectorial de velocidad:
v(t) = dr/dt = < -8*sen( (2π/5)*t )*(2π/5) , 8*cos( (2π/5)*t )*(2π/5) , 3 >,
resuelves componentes, y queda:
v(t) = < -(16π/5)*sen( (2π/5)*t ) , (16π/5)*cos( (2π/5)*t ) , 3 >.
Luego, derivas nuevamente, y tienes la expresión de la función vectorial de aceleración:
a(t) = dv/dt = < -(16π/5)*cos( (2π/5)*t )*(2π/5) , -(16π/5)*sen( (2π/5)*t )*(2π/5) , 0 >,
resuelves componentes, y queda:
a(t) = < -(32π2/25)*cos( (2π/5)*t ) , -(32π2/25)*sen( (2π/5)*t ) , 0 >.
Luego, plantea para la tangente del ángulo determinado por el vector velocidad y el plano OXY:
tan(α) = vz/√(vx2 + vy2),
donde tienes:
vz = 3,
√(vx2 + vy2) = √( (16π/5)2 ) = 16π/5,
luego, sustituyes en la expresión remarcada, y queda:
tan(α) = 3/(16π/5) = 15/(16π),
luego, compones en ambos miembros con la función inversa de la tangente, y queda:
α ≅ 16,616°.
Espero haberte ayudado.
-
Mikel Delgado
el 13/10/17Los bomberos están lanzando un chorro de agua a un edificio en llamas, utilizando una manguera de alta presión que imprime al agua una rapidez de 25 m/s al salir por la boquilla. Una vez que sale de la manguera, el agua se mueve con movimiento de proyectil. Los bomberos ajustan el ángulo de elevación α de la manguera hasta que el agua tarda 3 s en llegar a un edificio que está a 45 m de distancia. Ignore la resistencia del aire y suponga que la boquilla de la manguera está a nivel del suelo.
a) Calcule el ángulo de elevación α.
b) Determine la rapidez y aceleración del agua en el punto más alto de su trayectoria.
c) ¿A qué altura sobre el suelo incide el agua sobre el edificio, y con qué rapidez lo hace?
El apartado a) consigue sacarlo, me da un ángulo de elevación de 53,1º; pero no consigue sacar los siguientes, ya que en el punto más alto yo considero que la velocidad final sería nula, pero no es así, y no consigo plantear el problema.
Raúl RC
el 14/10/17Usando la formula en el eje y: V=Vo+gt
Reemplazando:
V=20-10(3)
V=-10m/s .... el signo menos significa que en 3 segundos el chorro de agua esta bajando.
Vx=25cos53°=15m/s
Vy=10m/s
Resultante de la velocidad=5√13 m/s
la aceleracion es 10 m/s2, positivo porque el chorro esta de bajada.
c) usando la formula: h=Vot+gt²/2
h=20(3)-10(3)²/2
h=15mmejor?
-
Mikel Delgado
el 13/10/17Dentro de una nave espacial en reposo sobre la Tierra, una pelota rueda desde la parte superior de una mesa horizontal y cae al piso a una distancia D de la pata de la mesa. Esta nave espacial ahora desciende en el inexplorado Planeta X. El comandante hace rodar la misma pelota desde la misma mesa con la misma rapidez inicial que en la Tierra, y se da cuenta de que la pelota cae al piso a una distancia 2.76D de la pata de la mesa. ¿Cuál es la aceleración debida a la gravedad en el planeta X?
Agradecería ayuda
Antonio Silvio Palmitano
el 13/10/17Considera un sistema de referencia con eje OX sobre el suelo, eje OY vertical, y considera que la altura de la mesa es H.
Luego, plantea las ecuaciones de movimiento de Tiro Oblicuo (o Parabólico):
En la Tierra:
x = v0*t
y = H - (1/2)*gT*t2,
reemplazas las coordenadas del punto de alcance (x = D, y = 0), y queda:
D = v0*t, de aquí despejas: D/v0 = t
0 = H - (1/2)*gT*t2,
luego sustituyes en la segunda ecuación, y queda:
0 = H - (1/2)*gT*D2/v02 (1).
En el Planeta X:
x = v0*t
y = H - (1/2)*gT*t2,
reemplazas las coordenadas del punto de alcance (x = 2,76*D, y = 0), y queda:
2,76*D = v0*t, de aquí despejas: 2,76*D/v0 = t
0 = H - (1/2)*gX*t2,
luego sustituyes en la segunda ecuación, y queda:
0 = H - (1/2)*gX*2,762*D2/v02,
resuelves coeficientes en el segundo término, y queda:
0 = H - 3,8088*gX*D2/v02 (2).
Luego, restas miembro a miembro entre las ecuaciones señaladas (1) (2), y queda:
0 = 3,8088*gX*D2/v02 - (1/2)*gT*D2/v02,
divides por D2 y multiplicas por v02 en todos los términos de la ecuación, y queda:
0 = 3,8088*gX - (1/2)*gT,
haces pasaje de término, y queda:
-3,8088*gX = - (1/2)*gT,
haces pasaje de factor como divisor, resuelves, y queda
gX ≅ 0,1313*gT,
reemplazas el valor del módulo de la aceleración gravitatoria terrestre, y queda:
gX ≅ 0,1313*9,8 ≅ 1,2865 m/s2.
Espero haberte ayudado.
-
Miss Legolas
el 13/10/17Hola! He estado intentando este ejercicio del péndulo simple pero no se si lo estoy haciendo bien o mal, porque no lo acabo de entender. ¿Podríais echarme una mano?
Un péndulo constituido por una masa de 0'5 kg cuelga de un hilo de 1 metro de longitud. Oscila con una amplitud de 8º en un lugar con gravedad 9'8 m/s2 . Calcula la energía potencial máxima y la velocidad máxima.
Gracias!
Raúl RC
el 14/10/17 -
Marta Sb
el 13/10/17
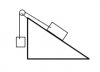Buenas tardes. ¿Alguien sería tan amable de ayudarme con este ejercicio? He probado en los dos sentidos y siempre me sale la aceleración negativa, no sé qué estaré haciendo mal o si tengo que interpretar el ángulo como -30º para que me dé positiva.Calcula la aceleración del sistema y la tensión en cada caso. Las masas son 10 kg y 5 kg y el coeficiente de rozamiento 0,2. Los planos inclinados forman triángulos rectángulos con uno de sus ángulos de 30º.
necronomicion00
el 13/10/17Cuando la aceleración, la velocidad o cualquier magnitud como estas te sale negativa, únicamente hace referencia a la dirección. Es decir, dependiendo de que direcciones has planteado en el problema te saldrá negativa o no. Pero en el fondo, si sólo te piden el valor de la aceleración, el resultado es el valor absoluto de la que te haya dado (Aún que en realidad se hace con el módulo). Todo esto lo digo suponiendo que en los planteamientos y cálculos lo tienes bien.
Un saludo!
Marta Sb
el 14/10/17Gracias, pero la cosa es que a mí siempre me enseñaron que si la aceleración me daba negativa en estos tipos de casos, era porque había escogido mal el sentido y tenía que hacer el problema entero con el sentido contrario... el problema es que ya lo he hecho en los dos sentidos y sigue dándome negativo. En el último momento me dio por poner que el ángulo era -30º por si cambiaba algo y sí me salió positivo, pero no sé si es por pura casualidad o porque de verdad se tiene que hacer así.
Mouad
el 14/10/17El signo como ha comentado antes, únicamente sirve para determinar el sentido de dicha magnitud, que esto lo verás más adelante cuando estudies dinámica en dos o tres dimensiones, dónde te saldrá la aceleración con sus respectivas componentes (i, j, k). Pero por ahora como te piden el módulo (el valor de la aceleración), si te sale el valor negativo quiere decir como tu has dicho que los sentidos los has tomado mal, pero eso no importa, ya que al final llegas al mismo resultado, sólo tendrás que poner la aceleración negativa.
Otra cosa que creo que es el problema que tienes, es que en realidad el ángulo que tienes no es de 30º. Si te fijas, ahora estás trabajando en el segundo cuadrante, y ese es el angulo (180 - α) que en este caso es (180 - 30), que es 150º. Prueba a repetir el mismo problema pero utilizando como angulo 150º. Si no has entendido bien lo que te he explicado en esta parte, te dejo una imagen donde verás los ángulos en cada cuadrante. Pero antes de todo, déjame explicarte que en el segundo cuadrante, los cosenos de cualquier ángulo es negativo. Entonces como estás en el segundo cuadrante, el coseno de 30º aquí es negativo. El seno sigue siendo positivo ya que el seno es negativo sólo en el tercer y cuarto cuadrante. Pero vaya, el ángulo no lo tomes como (-30), que aún que coincidan los resultados, en realidad estás tomando otro ángulo. (-30º = 330º)
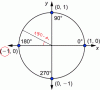
Cualquier cosa que no me haya explicado bien, dímelo y te lo explico más detalladamente. Un saludo!
-
paola
el 13/10/17Buenas tardes. ¿Sería alguien tan amable de echarme una mano con los apartados d y e del ejercicio 7 y el e y f del 9? He resuelto ambos problemas hasta ese punto pero a partir de ahí no sé cómo seguir... Urge la ayuda :)
-
Matías Gonzalez
el 13/10/17Hola, si yo tengo una esfera cuyo volumen es de 7 m3, pesa 1820 N y sostiene encima otro cuerpo que pesa 385 N, ¿cuanto debe pesar un bloque que cuelga de la esfera para que la hunda hasta la mitad en agua de mar?
