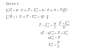-
CONSULTA:
- UNOS RIELES DE 12m DE LONGITUD SE COLOCAN UN DIA DE INVIERNO EN QUE LA TEMPERATURA DEL AIRE ES 32ºF.
SE PIDE DETERMINAR QUE ESPACIO HABRIA QUE DEJAR ENTRE ELLOS PARA QUE UN DIA EN QUE LA TEMPERATURA ES DE 40ºC. LA TENSION ENTRE ELLOS SEA T= 1200kg/cm2 ; alfa= 12 x 10exp-6 x 1/ºC ; E=2,1 x 10exp6 kg/cm2
Muchas gracias!
Raúl RC
el 16/9/17Hola! Me encantaría ayudarte, pero no respondemos dudas universitarias que no tengan que ver específicamente con los videos que ya ha grabado como excepcion el profe. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
CONSULTA:
- PARA LLENAR DE AGUA UN TANQUE (rendimiento de la bomba 20%) UBICADO A 20m DE ALTURA SE CONSUME 15kwh DE ENERGIA.
SE PIDE DETERMINAR LOS LITROS DE AGUA ALMACENADOS EN EL TANQUE.
Muchas gracias!
Antonio Silvio Palmitano
el 15/9/17Tienes la energía consumida por la bomba:
U = 15 KWh = 15*1000*3600 = 54000000 J.
Tienes que en el enunciado, la energía entregada a la masa de agua es:
Ue = 0,20*U = 0,20*54000000 = 10800000 J.
Luego, observa que la energía entregada por la bomba queda almacenada como energía potencial gravitatoria de la masa de agua elevada al tanque, por lo que puedes plantear:
EPg = Ue, sustituyes y queda:
M*g*h = Ue, reemplazas valores y queda:
M*9,8*20 ≅ 10800000, haces pasajes de factores y queda:
M ≅ 55102,041 Kg, que es la masa de agua elevada al tanque.
Luego, plantea la relación entre masa de agua y volumen (indicamos con δ a la densidad del agua):
δ*V = M, haces pasaje de factor como divisor y queda:
V = M/δ, reemplazas valores y queda:
V ≅ 55102,041/1000 = 55,102041 m3 = 55102,041 dm3 = 55102,041 litros.
Espero haberte ayudado.
-
ayuda porfavor
a. Valores de resistencia entre 1kΩ y 5kΩ
b. Voltaje en el terminal 3 es la tercera parte del voltaje en la terminal 1.
c. Si requiere valores de resistencia por fuera del rango dado, debe justificar la razón de los mismos y tomarlos por arriba de los valores dados.
debe calcular.
-Los voltajes en cada resistencia
-La corriente total del circuito.
-El voltaje en el terminal 1, 2 y 3.
-La potencia consumida por cada resistencia y entregada por la fuente de alimentación.
- Si se conectan los dispositivos en paralelo y se desea colocar un elemento de protección, ¿cuál sería la corriente que debería soportar?
agradezco
Francisco Javier
el 15/9/17Es el mismo problema que te resolví hace unos días, solo que con más preguntas.
De mi respuesta anterior te recuerdo que elegimos valor de 1 kΩ para todas las resistencias.
Esto nos hacía tener una corriente total de 2.25 mA.
También calculamos el voltaje del punto tres, que fue V3 = 2.25 V.
Si no recuerdas el procedimiento para esto antes dicho, agradecería que te fijaras en la primera respuesta que te dí. Allí lo resuelvo detalladamente.
La intensión es no voy a escribir lo mismo dos veces.
Ahora, como novedad aquí se te pide el voltaje en cada resistencia. Esto es sencillo.
Debido a que todas las resistencias tienen un mismo valor y por todas pasa la misma corriente, todas tendrán un mismo voltaje.
Aplicando Ley de Ohm, V = I*R, damos con el voltaje en cada resistencia.
V = It*R = 2.25m*1k = 2.25 V.
Todas las resistencias tienen un voltaje de 2.25 V.
El voltaje en el punto dos y tres se obtienen haciendo un recorrido que empieza en dicho punto y termina en tierra. Te vendría bien repasar Kirchhoff si no entiendes este paso:
V1 = (R + R + R)*It = (3R)*It = 3*1k*2.25m = 6.75 V → V1 = 6.75 V
V2 = (R + R)*It = (2R)*It = 2*1k*2.25m = 4.5 V → V2 = 4.5 V
La potencia en cada resistencia, al igual que el voltaje, es la misma en todas por la misma razón que dimos anteriormente. Comparten todas mismas características.
Para resistencias, la potencia se halla aplicando: P = R*I2
Entonces:
P = 1k*(2.25m)2 = 0.0050625 W.
Todas las resistencias disipan una potencia de 0.0050625 W.
La potencia entregada por la fuente será la suma de cada potencia en las resistencias. Multiplicamos la potencia de cada resistencia por cuatro (ya que hay cuatro resistencias):
Pt = 0.0050625*4 = 0.02025 W.
Se pudo hallar este valor también aplicando la ecuación: P = I*V
Tenemos el valor de la fuente y la corriente que circula por el (que es la corriente total). Se debe obtener el mismo valor:
Pt = 2.25m*9 = 0.02025 W.
La fuente entrega una potencia de 0.02025 W.
Si conectamos las resistencias en paralelo, habrá que calcular la nueva resistencia equivalente vista por la fuente.
Recuerda que para sumar resistencias en paralelo se usa:
1/Req. = 1/R1 + 1/R2 + 1/R3 + ... + 1/RN
Entonces:
1/Req. = 1/1k + 1/1k + 1/1k + 1/k
1/Req. = 1/250
Req. = 250 Ω
Y aplicando Ley de Ohm hallamos la nueva corriente total:
V = It*Req.
It = V/Req.
It = 9/250
It = 36 mA
-
Antonio Silvio Palmitano
el 13/9/17Debes tener en cuenta que sobre el cuerpo con masa M2 actúan cinco fuerzas, de las indicamos sus módulos direcciones y sentidos:
Fuerza exterior: F, paralela al plano inclinado, hacia arriba:
Tensión de la cuerda: T, paralela al plano inclinado, hacia abajo;
Rozamiento: fr2 = μN2, paralela al plano inclinado, hacia abajo;
Peso: P2 = M2g, vertical, hacia abajo, que forma un ángulo de 30° con la dirección perpendicular al plano inclinado;
Acción Normal del plano inclinado: N2, perpendicular al plano inclinado, hacia arriba;
luego, establece un sistema de referencia con eje OX paralelo al plano inclinado y sentido positivo hacia arriba, y eje OY perpendicular al plano inclinado, con sentido positivo hacia arriba,
luego plantea la Primera Ley de Newton (observa que los bloques se desplazan con velocidad constante) y queda el sistema de ecuaciones:
F - P2*sen(30°) - T - fr2 = 0
N2 - P2*cos(30°) = 0;
luego sustituyes expresiones en ambas ecuaciones y queda:
F - M2g*sen(30°) - T - μN2 = 0 (1)
N2 - M2g*cos(30°) = 0 (2)
Debes tener en cuenta que sobre el cuerpo con masa M1 actúan cuatro fuerzas, de las indicamos sus módulos direcciones y sentidos:
Tensión de la cuerda: T, paralela al plano inclinado, hacia arriba;
Rozamiento: fr1 = μN1, paralela al plano inclinado, hacia abajo;
Peso: P1 = M1g, vertical, hacia abajo, que forma un ángulo de 30° con la dirección perpendicular al plano inclinado;
Acción Normal del plano inclinado: N1, perpendicular al plano inclinado, hacia arriba;
luego, establece un sistema de referencia con eje OX paralelo al plano inclinado y sentido positivo hacia arriba, y eje OY perpendicular al plano inclinado, con sentido positivo hacia arriba,
luego plantea la Primera Ley de Newton (observa que los bloques se desplazan con velocidad constante) y queda el sistema de ecuaciones:
- P1*sen(30°) + T - fr1 = 0
N1 - P1*cos(30°) = 0;
luego sustituyes expresiones en ambas ecuaciones y queda:
- M1g*sen(30°) + T - μN1 = 0 (3)
N1 - M1g*cos(30°) = 0 (4).
Luego, con las ecuaciones señaladas (1) (2) (3) (4) tienes el sistema:
F - M2g*sen(30°) - T - μN2 = 0 (1)
N2 - M2g*cos(30°) = 0 (2)
- M1g*sen(30°) + T - μN1 = 0 (3)
N1 - M1g*cos(30°) = 0 (4),
cuyas incógnitas son: F, T, N2, N1,
reemplazas valores conocidos (consideramos: g = 9,8 m/s2) y queda:
F - 98*sen(30°) - T - 0,5*N2 = 0 (1)
N2 - 98*cos(30°) = 0 (2)
- 98*sen(30°) + T - 0,5*N1 = 0 (3)
N1 - 98*cos(30°) = 0 (4),
y solo queda que resuelvas el sistema de ecuaciones.
Espero haberte ayudado.
-
¿Alguien me puede explicar esta actividad? Gracias.
¿En que punto de la linea que une dos masas, una el triple que la otra, se anula la g (con flecha arriba, la intensidad del campo gravitatorio) total?
Antonio Silvio Palmitano
el 13/9/17Puedes llamar M1 y M2 a las masas de las dos partículas, y puedes llamar d a la distancia que las separa.
Luego, puedes llamar r a la distancia entre el punto en estudio y la partícula con masa M1 (observa que r es menor que d) y tienes que la distancia entre la partícula con masa M2 y el punto en estudio es d-r.
Luego, haz un gráfico y verás que los campos gravitatorios producidos por las partículas en el punto en estudio tienen la misma dirección, pero tienen sentidos opuestos.
Luego, tienes en tu enunciado la relación entre las masas de las partículas: M1 = 3*M2 (1).
Luego, plantea los módulos de los campos gravitatorios producidos por las partículas en el punto en estudio (observa que indicamos con G a la constante de gravitación universal):
g1 = G*M1/r2,
g2 = G*M2/(d-r)2.
Luego, como tienes en el enunciado que el campo gravitatorio resultante en el punto en estudio es es nulo, puedes plantear:
g1 - g2 = 0, haces pasaje de término y queda
g1 = g2, sustituyes las expresiones de los módulos de los campos gravitatorios y queda:
G*M1/r2 = G*M2/(d-r)2, divides en ambos miembros por G, haces pasajes de divisores como factores, y queda:
M1*(d-r)2 = M2*r2 , sustituyes la expresión señalada (1) en el primer miembro, y queda:
3M2*(d-r)2 = M2*r2 , divides en ambos miembros por M2, y queda:
3(d-r)2 = r2 , desarrollas el binomio elevado al cuadrado y queda:
3(d2 - 2d*r + r2) = r2, distribuyes en el primer miembro, haces pasaje de término, y queda
3d2 - 6d*r + 2r2 = 0, ordenas términos y queda:
2r2 - 6d*r + 3d2 = 0, que es una ecuación polinómica cuadrática, cuyas soluciones para la incógnita r quedan:
r = ( 6d ± √(36d2 - 24d2) )/4 = ( 6d ± √(12d2) )/4 = ( 6d ± √(12)d )/4 = ( 6 ± √(12) )d/4,
por lo que tienes dos opciones:
a)
r = ( 6 + √(12) )d/4 ≅ 2,3660d, que es mayor que d, por lo que no tiene sentido para este problema;
b)
r = ( 6 - √(12) )d/4 ≅ 0,6340, que es menor que d, y si tiene sentido para este problema.
Espero haberte ayudado.
Pau Fajardo Sevilla
el 13/9/17Antonio Silvio Palmitano
el 13/9/17Tienes razón, Pau.
La respuesta correcta es: r ≅ 0,6340d.
Perdona el error al escribir la respuesta.
Con respecto a la distancia entre las partículas (d) esta no está consignada en el enunciado, por lo que la distancia entre el punto en estudio y la partícula con masa M1 queda expresada como hemos remarcado.
-
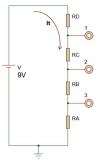
Esque no soy experimentado en esto de circuitos y la verdad necesito ayuda.Dispositivo 2 - Requiere las siguientes condiciones:a. Valores de resistencia entre 1kΩ y 5kΩ b. Voltaje en el terminal 3 es la tercera parte del voltaje en la terminal 1. c. Si requiere valores de resistencia por fuera del rango dado, debe justificar la razón de los mismos y tomarlos por arriba de los valores dados.agradezco si me puede orientar dando esos valore
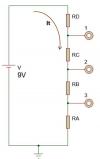
Francisco Javier
el 13/9/17Puedes darle valor de 1 kΩ a todas las resistencias.
RA = RB = RC = RD = R = 1 kΩ.
Dicho esto, podemos hallar la corriente que circula por el circuito haciendo la respectiva ecuación de malla:
(R + R + R + R)*It - V = 0
(4R)*It = V
It = V/4R
It = 9/4*1k
It = 2.25 mA
Tenemos que se debe cumplir que el voltaje en el terminal tres debe ser igual a un tercio del voltaje en el terminal uno. Matemáticamente.
V3 = (1/3)*V1
Pero V1 lo podemos calcular haciendo un recorrido desde dicho punto a tierra. Sale:
V1 = (R + R + R)*It
V1 = (3R)*It
V1 = (3*1k)*2.25m
V1 = 6.75 V
Entonces:
V3 = (1/3)*6.75
V3 = 2.25 V
Este es un valor de diseño y debemos demostrar que realmente esto es cierto. Para eso calculamos V3 como debería ser. Partiendo desde punto tres a tierra:
V3 = R*It
V3 = 1k*2.25m
V3 = 2.25 V
Los voltajes son iguales, por lo que la suposicion es correcta. No fue necesario utilizar valores de resistencias mayores a 5 kΩ.
Puedes ver que este procedimiento se cumple siempre y cuando escojas los valores de resistencias todos iguales.
Quiere decir que puedes tambien decir que todas las resistencias valen 2kΩ, 3kΩ, etc.
Hay otras combinaciones que puedes hacer, pero esta es la mas facil.
-
Buenas,
¿Alguien me podria dar una formula de la dsitancia en funcion de la velocidad, tiempo, aceleracion y posicion inicial, para un movimiento uniformemente acelerado?
Antonio Silvio Palmitano
el 12/9/17El colega Fermat te ha indicado la expresión de la función de posición de Movimiento Rectilíneo Uniformemente Variado, con la consideración que el instante inicial es t0 =0:
s = s0 + v0*t + (1/2)*a*t2 (posición en función del tiempo);
luego derivas con respecto al tiempo y tienes:
v = v0 + a*t (velocidad en función del tiempo);
luego, puedes despejar el tiempo en la ecuación de velocidad y queda: (v - v0)/a = t,
reemplazas en la expresión de la función posición y queda:
s = s0 + v0*(v - v0)/a + (1/2)*a*(v - v0)2/a2,
distribuyes el segundo término, desarrollas el tercer término, y queda:
s = s0 + v0*v/a - v02/a + (1/2)*v2/a - v*v0/a + (1/2)*v02/a,
cancelas tér minos opuestos, reduces términos semejantes, y queda:
s = s0 - (1/2)*v02/a + (1/2)*v2/a,
haces pasaje de término y queda:
s - s0 = - (1/2)*v02/a + (1/2)*v2/a,
ordenas términos y extraes factor común y divisor común en el segundo miembro y queda:
s - s0 = (1/2)*(v2 - v02)/a,
multiplicas en ambos miembros por 2*a y queda:
2*a*(s - s0) = v2 - v02,
que es una ecuación implícita de la posición como función de la velocidad (observa que no depende del tiempo.
Espero haberte ayudado.
-
Muy buenas. Perdonen pero hay una cuestión que no comprendo y por más q busco no hallo una explicación.
La situación: Existe un plano inclinado, y un objeto (redondo: una esfera o un cilindro) rueda por él.
Mi pregunta: La fuerza de rozamiento HACIA DÓNDE VA????? Es que en sitios leo que como en la opción 1 y en otros me ha parecido entender que como en la 2, y no entiendo nada! Si se opone al movimiento del cuerpo, que es de rodadura, no debería ser como en la 2? Pero luego leo que no, que es como en la primera. A lo mejor depende de si el cuerpo rueda o se desliza, si no no lo he entiendo. Por favor si alguien pudiera explicármelo estaría muy agradecido!!
Es que por este motivo no se resolver este ejercicio, a ver si alguien me puede ayudar con él:
Muchas gracias de antemano!
Raúl RC
el 11/9/17Te recomiendo veas este vídeo que grabó, como excepción, el profe, pues tu problema es propio de nivel universitario y de momento unicoos no los aborda, lo lamento
https://www.unicoos.com/video/fisica/universidad/dinamica/momento-de-inercia/rotacion-en-un-plano-inclinado-momento-de-inercia
Fermat
el 12/9/17Hola César. Es la opción 2, si el objeto rueda en un plano inclinado con rozamiento, en este caso en sentido horario, eso quiere decir que va a existir una fuerza de rozamiento que se oponga a la rotación y es inmediato pensar que, tratándose de rotaciones, se oponga en sentido antihorario. Justamente lo que ilustra la opción 2.
Fermat
el 12/9/17César Reina Moreno
el 13/9/17Vale, muchísimas gracias por contestar!! Pero una cosa. Entonces la Fuerza de rozamiento siempre se opone al sentido en el que ruede el cuerpo.. por qué en el vídeo que ha puesto arriba Raúl RC (https://www.unicoos.com/video/fisica/universidad/dinamica/momento-de-inercia/rotacion-en-un-plano-inclinado-momento-de-inercia) David pone la fuerza de rozamiento hacia arriba del plano, cuando el cuerpo rueda hacia abajo??? ahí no estaría al revés, es decir, a favor del giro?? o a lo mejor es que esa fuerza de rozamiento va ligada a la tensión de la cuerda, y no depende de si el objeto gira o no?? De verdad siento mucho la torpeza y las molestias!!
P.D. Y otra cosa, en el primer ejercicio que has puesto, de donde sale el cos de la primera linea? La F (tension) no era paralela al plano?
Por cierto, la asignatura es Física I de primero en ingeniería, que son prácticamente los mismos temas que en bach pero añaden algo más. De hecho, sigo estudiando con los libros del instituto.
-
hola unicoos necesito ayuda y que me expliquen este ejercicio de movimiento relativo (cinematica en 2 dimensiones)