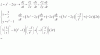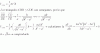-
Hola, unas dudas más (perdón esque mañana rindo y mi profe no me aclaró las dudas)
Cuales son los autovalores de una matriz de proyección? Y cuales de una matriz de simetría? Justifique las respuestas
Guillem De La Calle Vicente
el 23/6/18 -
Guillem De La Calle Vicente
el 22/6/18¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
Alguien me podría ayudar con este problema:
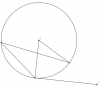
En la circunferencia de centro en O, sabemos que el alguno ABC mide 29°. Calculá los ángulos
El punto a) sé que mide 56°, ya que el ángulo AOC es el central correspondiente al ángulo inscripto (que mide 29).
El punto b), sé que mide 90°, pero no sé cómo probarlo. ¿como puedo justificar que mide 90°?
Gracias
-
hola, alguien puede ayudarme con el siguiente ejercicio, gracias.
-Un examen tipo test consta de 10 preguntas y cada pregunta puede responderse con 4 opciones.
A) Si no dejamos ninguna pregunta en blanco, ¿de cuantas formas distintas puede responderse?
B) Supongamos que respondemos cada pregunta de modo aleatorio.¿Cual es la probabilidad de aprobar; esto es, de acertar 5 o más preguntas?
Antonio Silvio Palmitano
el 22/6/18A)
Observa que por cada pregunta tienes 4 opciones, por lo que por el principio de multiplicación que la cantidad de respuestas posibles queda:
NA = 4*4*4*4*4*4*4*4*4*4 = 410.
B)
Observa que la probabilidad de acertar una pregunta es: p = 1/4 = 0,25,
cuya probabilidad complementaria es: q = 1 - p = 3/4;
y observa que tienes en total n = 10 preguntas, que se responden independientemente.
Por lo tanto, puedes definir la variable aleatoria discreta:
X: "cantidad de preguntas acertadas",
y observa que la variable toma valores naturales desde 0 hasta 10 inclusive;
por lo que tiene una distribución binomial, con parámetros: n = 10 y p = 0,25,
con la probabilidad complementaria: q = 0,75,
cuya función de distribución tiene la expresión:
p(X=k) = C(10,k)*pk*q10-k,
reemplazas los valores de las probabilidades, y queda:
p(X=k) = C(10,k)*0,25k*0,7510-k, con k ∈ N, 0 ≤ k ≤ 10.
Luego, tienes que calcular:
p(X ≥ 5) =
= p(X = 5) + p(X = 6) + p(X = 7) + p(X = 8) + p(X = 9) + p(X = 10);
luego, sustituyes las expresiones de los términos según la expresión de la función de distribución, y queda:
p(X ≥ 5) =
= C(10,5)*0,255*0,7510-5 + C(10,6)*0,256*0,754 + C(10,7)*0,257*0,753 +
+ C(10,8)*0,258*0,752 + C(10,9)*0,259*0,751 + C(10,10)*0,2510*0,751;
y solo queda que hagas el cálculo.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 22/6/18Tienes la ecuación diferencial (observa que expresamos a la función derivada como cociente entre diferenciales):
e3-x^2 * dy/dx = 2*x*(y - 3).
Luego, separas variables, y queda:
dy/(y-3) = 2*x*dx/e3-x^2.
Aplicas la propiedad de las potencias con exponente negativo en el segundo miembro, y queda:
dy/(y-3) = 2*x*dx*e-(3-x^2).
En el segundo miembro aplicas la sustitución (cambio de variable):
w = -(3-x2) (1),
de donde tienes:
dw = 2*x*dx;
luego, sustituyes y la ecuación diferencial queda:
dy/(y-3) = dw/w.
Integras en ambos miembros, y queda:
ln(y-3) = ln(w) + c,
expresas a la constante de integración como el logaritmo de una constante positiva, y queda:
ln(y-3) = ln(w) + ln(C),
aplicas la propiedad del logaritmo de una multiplicación, y queda:
ln(y-3) = ln(K*w),
compones en ambos miembros con la función inversa del logaritmo natural, y queda:
y - 3 = K*w,
sumas 3 en ambos miembros, y queda:
y = K*w + 3,
sustituyes la expresión señalada (1), y queda:
y = K*( -(3-x2) ) + 3,
distribuyes el primer término, ordenas términos, y queda:
y = K*x2 - 3*K + 3,
que es la expresión explícita de la solución general de la ecuación diferencial que tienes en tu enunciado.
Espero haberte ayudado.
-
Buenos días : tengo una duda, ¿porque el siguiente intervalo tiene intersección vacía? Me pueden ejemplificar . Es en referencia al principio de intervalos encajados .
la familia de intervalos {\displaystyle I_{k}=(0,2^{-k}),k\in \mathbb {N} } es una familia de intervalos todos ellos no vacíos pero con intersección vacía.