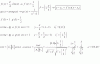-
diferencial y'+y=sen(X)y valor de C para que cumpla y(pi/2)=1
Antonio Silvio Palmitano
el 13/6/18Tienes la ecuación diferencial lineal, de primer grado, no homogénea:
y ' + 1*y = senx;
cuya solución general queda expresada:
y = e-x * ( ∫ ex*senx*dx + C );
luego, resuelves la integral del argumento (observa que debes plantear el Método de Integración por Partes en dos pasos, y que la integral es recursiva), y queda:
y = e-x * ( (1/2)*ex*senx - (1/2)*ex*cosx + C );
luego, distribuyes, y queda:
y = (1/2)*senx - (1/2)*cosx + C*e-x,
que es la solución general de la ecuación diferencial expresada en forma explícita.
Luego, tienes la condición inicial: x = π/2, y = 1, reemplazas valores, y queda:
1 = (1/2)*1 - (1/2)*0 + C*e-π/2, cancelas el término nulo, restas 1/2 en ambos miembros, y queda:
1/2 = C*e-π/2, multiplicas en ambos miembros por eπ/2, y queda:
(1/2)*eπ/2 = C,
luego, reemplazas el valor remarcado en la expresión de la solución general, y queda:
y = (1/2)*senx - (1/2)*cosx + (1/2)*eπ/2*e-x,
que es la solución particular de la ecuación diferencial con la condición indicada en tu enunciado, expresada en forma explícita.
Espero haberte ayudado.
-
Antonio
el 13/6/18De ahí puedes demostrar que la X=4 es solución del polinomio. Recuerda que es (x-4) y al despejar x=4.
Entonces el polinomio factorizado una vez te queda (x-4) (x2 + 4x + 16)
Después con los números que has ido bajando al operar puedes formar una ecuación de segundo grado (x2 + 4x + 16) con la formula, o también puedes seguir sacando soluciones con Ruffini. Las soluciones son complejas, así que esa es la única solución real.
-
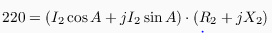 y
y 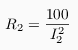 siendo A=-55.60º. Mi pregunta es ¿como lo despejo de ahí las incógnitas?
siendo A=-55.60º. Mi pregunta es ¿como lo despejo de ahí las incógnitas?Lo que se es que da I2=0,80 X2= 225,61 R2= 154,47 pero no obtengo lo mismo.
David
el 21/6/18Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Buenos días de nuevo UNICOOS, estoy terminando con este tema de PROPIEDADES DE LOS DETERMINNANTES y tengo una duda con este ejercicio (anexo foto); lo logré resolver reduciéndolo por la primera fila (foto 1), pero luego intenté separar el determinante como una suma y el resultado me da diferente, es más no puedo resolver la ecuación bicuadrática que me sale (foto 2). Alguien puede decirme, por favor, ¿qué he hecho mal en esa separación del determinante o esa propiedad no se puede aplicar así?.
Gracias de antemanno por la ayuda.
-
Alguien me podría resolver la opción A? He hecho hoy el examen y estoy en dudas en todos los apartados...muchas gracias!!!!
David
el 21/6/18 -
David
el 21/6/18Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
¯\_(?)_/¯
el 13/6/18Antes de todo este problema se puede resolver de varias maneras, en mi opinión la más adecuada sería hallar las ecuaciones de las rectas tangentes por los puntos de intersección de f1(x) y f2(x) aplicando la ecuación punto-pendiente y = [f'(Xo) (X-Xo)] + f(Xo) donde f'(Xo) es la derivada de la funcion el punto Xo y f(Xo) la imagen o la "y" de dicho punto despues realizar el productor vectorial con vectores directores de ambas rectas (Ux , Uy) • (Vx , Vy) = |U||V| cos α y despejar el cos α.
Como f1(x) = ln (x) + π/4 su derivada f'1(x) = 1/x por otro lado la imagen para x = 1 es π/4 ya que f(1) = ln (1) + π/4 = 0 + π/4 = π/4 en consecuencia y1 = (1/1)(x-1) + π/4 = x - [(4 - π) / 4]En el caso de f2(x) = arc tg (x) habría que hacer lo mismo, quedándonos y = (1 / 1 + 12 ) (x-1) + π/4 = (1/2)x + [-(1/2) + (π/4)] = (1/2)x - [(2 - π) / 4]
Una vez tenemos la ecuacion de estas dos rectas simplemente sacamos los vectores directores "u" y "v" de cada recta, a partir de las pendientes de estas, como la pendiente m = (y /x) el vector director "d" de una recta será d(Dx , Dy) es decir siendo Dx el denominador y Dy el numerador de la pendiente.
Por tanto el vector director "u" de la recta tangente y1 sería u(1 , 1) mientras que el vector director "v" de la recta tangente y2 sería v(2, 1) realizando el producto escalar nos quedaría 1×2 + 1×1 = [(12+12) (12+22)]^½ cos α ---> 2+1 = (10)^½ cos α ---> cos α = [3 / (10)^½] = [(3)(10)^½ / 10]
P.D se me olvidó mencionar que en el producto escalar |U| y |V| son los modulos de dichos vectores directores, el módulo de cualquier vector en el plano es |D|= (Dx2 + Dy2)^½ no sé muy bien como utilizar el foro aún así que para expresar las raíces cuadradas utilizo ^½
-
Hola, agradecería vuestra ayuda, no entiendo por qué en el numerador pone 1 , o sea, entiendo que f(x,y) es x+y <= 1 , entonces si f(y), que es lo que va en el denominador, es 1-x, al despejar, lo que nos queda es x, no debería estar x en el numerador? creo que me estoy liando xd.
Os podría resumir mi duda en esta pregunta: en las distribuciones condicionadas de X/Y=y y viceversa, ¿Por qué se pone un 1 en el denominador en este ejercicio?
Gracias de antemano.
David
el 21/6/18Me encantaría ayudarte, pero no respondemos dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)