-
Alejandro
el 13/6/18Mi pregunta es concreta... para un sistema compatible indeterminado (de infinitas soluciones), al resolverlo,¿ siempre hay que triangular la matriz antes de dar valores a una incógnita?
Lo digo por este ejemplo
x+2y=3
-x+2z=-1
Para este sistema se le puede dar valor alfa a z y ya sustitur en el resto... repito, ¿es necesario hacer triangulación de la matriz antes de dar valores? porque si hago cero en la segunda ecuación, al final me da otro valor distinto. No debería dar el mismo resultado si triangulo a si no triangulo la matriz?
Gracias.
Antonio Silvio Palmitano
el 13/6/18No es necesario llegar a la triangulación, y si asignas un parámetro como sugieres, es más cómodo asignarlo a la incógnita que figura en ambas ecuaciones:
x = t,
t + 2y = 3, de aquí despejas: y = 3/2 - (1/2)*t,
-t + 2z = -1, de aquí despejas: z = -1/2 + (1/2)*t;
y la expresión de las soluciones del sistema queda:
x = t,
y = 3/2 - (1/2)*t,
z = -1/2 + (1/2)*t,
con t ∈ R.
Y si triangulas, llegarás a expresiones equivalentes.
Espero haberte ayudado.
-
Alvaro
el 13/6/18 -
Jorge
el 12/6/18 -
Portero
el 12/6/18Hola unicoos tengo una duda, ¿si hay en el cálculo de un límite cualquier indeterminación entonces se divide la función entre la X de mayor grado del numerador?
Guillem De La Calle Vicente
el 21/6/18 -
Andrea hdz
el 12/6/18Una duda, si a la hora de calcular el rango de una matriz de 3x3 lo hago mediante el menor adjunto y por tanto cálculo el rango de la matriz 2x2 que me queda y el rango me da distinto de 0 ¿El rango sería 3 o 2?
Antonio Silvio Palmitano
el 12/6/18Si quieres establecer el rango de una matriz de orden 3*3 por medio de determinantes, debes seguir estos pasos:
1°)
Calcula el determinante de la matriz, y tienes dos opciones:
a)
si es distinto de cero, entonces el rango de la matriz es 3;
b)
si es igual a cero, entonces el rango de la matriz es menor que 3.
2°)
Consideras los determinantes adjuntos de orden 2, y tienes dos casos:
a)
si uno de ellos es distinto de cero, entonces el rango de la matriz es 2;
b)
si todos ellos son iguales a cero, entonces el rango de la matriz es menor que 2.
3°)
Consideras los elementos de la matriz, y tienes dos casos:
a)
si uno de ellos es distinto de cero, entonces el rango de la matriz es igual a 1;
b)
si todos los elementos son iguales a cero, entonces tienes la matriz nula y su rango es igual a 0.
Espero haberte ayudado.
-
Laura
el 12/6/18Hola Unicoos! Necesito hallar por extensión la siguiente relación:
Sea A={1,2,3,4} y B ={ 1,2,3,4,5,6} hallar por extensión la relación: (x,y) ∈ ℛ↔y=3x
La relación esta incluida de AxB.
Antonio Silvio Palmitano
el 12/6/18Tienes la expresión por comprensión de la gráfica de la relación:
GR = { (x,y), x ∈ A, y ∈ B, y = 3x }.
Luego, observa que la segunda componente de los pares ordenados debe pertenecer al conjunto B, y observa también que debe se el triple de la primera componente, y esta primera componente debe pertenecer al conjunto A, por lo que la expresión de la gráfica de la relación por extensión queda:
GR = { (1,3), (2,6) };
y observa que los triples de 3 y 4 (que son 9 y 12) no pertenecen al conjunto B;
y observa que 1, 2, 4 y 5 no son los triples de elementos que pertenezcan al conjunto A.
Espero haberte ayudado.
-
jj jo (Jotonxu)
el 12/6/18
Alguien me ayuda con este problema de matematicas?
gracias
David
el 21/6/18Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
juan sebastian vega
el 12/6/18 -
Adriana Paredes
el 12/6/18 -
Lu Op
el 12/6/18
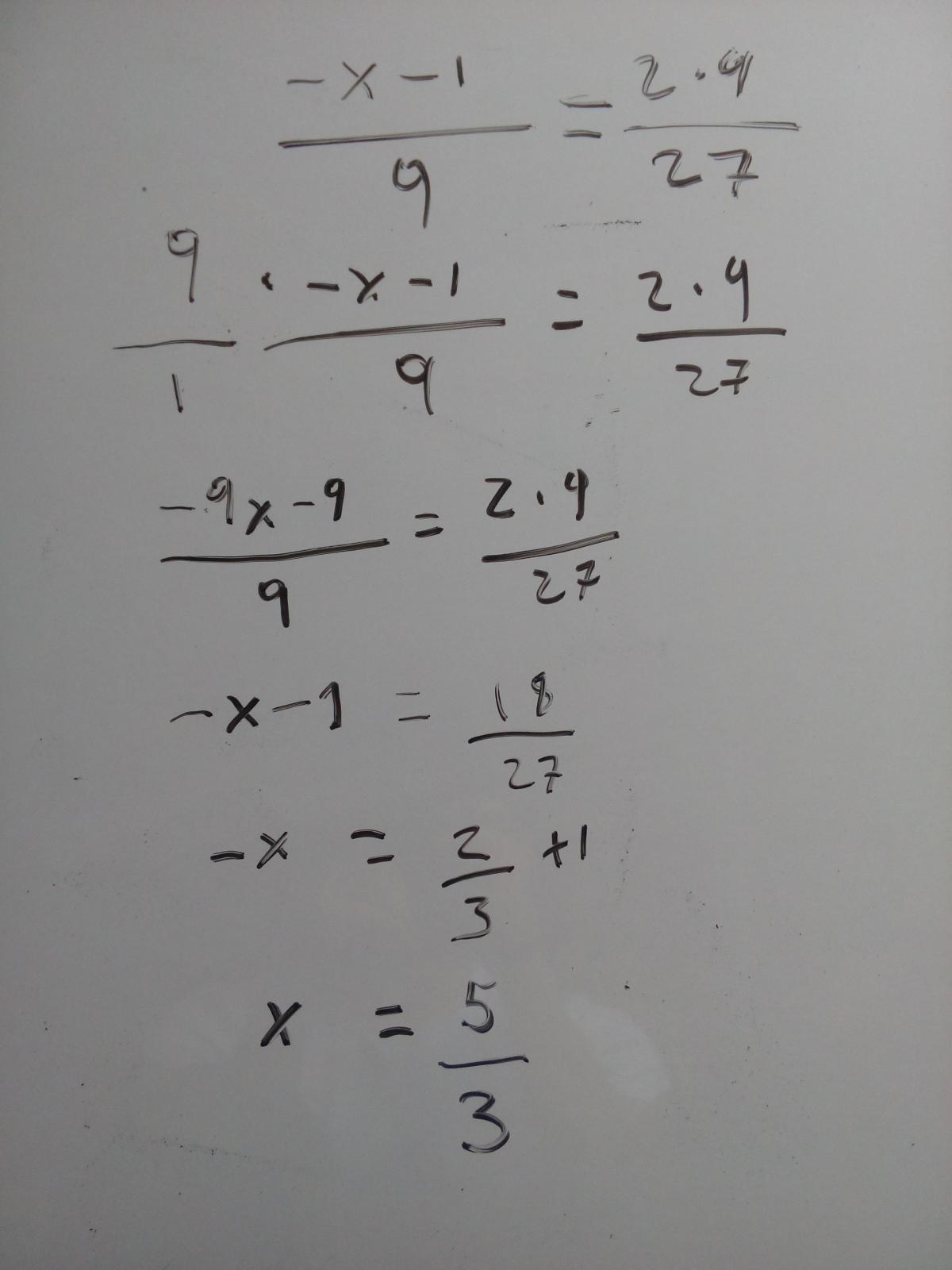Hola, este procedimiento es correcto?, en symbolab el (-x-1)/9 se transforma en un -x+1
