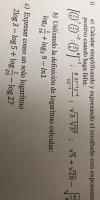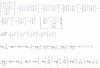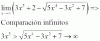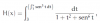-
Beatrice Pagnozza
el 12/6/18 -
Sheila Corrales Garcia
el 12/6/18 -
02pj _
el 12/6/18Hola! Podrían ayudarme con este problemita? Mañana tengo examen y no me sale
Hoy la edad de Lucas es la raíz cuadrada de la edad de Juan y dentro de 4 años la edad de Juan cuadruplicará a la de Lucas. ¿Qué edades tienen?
Antonio
el 12/6/18hoy:
la edad de Lucas es x años
la edad de Juan es y años
Hoy la edad de Lucas es la raíz cuadrada de la edad de Juan => x=√y
por otro lado, dentro de 4 años:
la edad de Lucas será x+4 años
la edad de Juan será y+4 años
dentro de 4 años la edad de Juan cuadruplicará a la de Lucas => y+4=4(x+4)
por lo que tenemos dos ecuaciones con dos incógnitas, es decir, un sistema de ecuaciones:
x=√y
y+4=4(x+4)
Solo queda resolverlo:
Con la segunda
y+4=4x+16
y=4x+12
Con la primerax=√y
sustituyendo
x=√(4x+12)
por lo tanto
x2=4x+12
x2-4x-12=0
Resolvemos esta ecuación de segundo grado
x=(-(-4)±√((-4)2-4·1·(-12)))/(2·1)=(4±√(64))/(2)=(4±8)/(2)=6 ^ -2
x=6 es solución pero x=-2 no es solución pues Lucas no puede tener esa edad
y finalmente obtenemos el valor de y
como x=√y => 6=√y => y=36
por lo tanto:
la edad de Lucas es 6 años
la edad de Juan es 36 años
fíjate que cumple las dos condiciones
-
Toni Serrano Jiménez
el 12/6/18 -
Interayuda
el 12/6/18Buenas tardes UNICOOS, les escribo porque tengo este problema del tema PROPIEDADES DE LOS DETERMINANTES que no me sale por ese método (propiedades de los determinantes), lo pude sacar por SARUS, pero la respuesta que plantean por propiedades no he logrado sacarla, en la foto están ambas respuestas.
Alguien puede decirme qué proiedad usar, las he intentado todas las que conozco.
Gracias.
Antonio Silvio Palmitano
el 12/6/18A la primera fila le sumas las otras dos filas, y el determinante queda:
D =
-x-1 -x-1 -x-1
-1 1-x -1
-1 -1 1-x.
Extraes factor común en la primer fila, y queda:
D = (x+1)*
-1 -1 -1
-1 1-x -1
-1 -1 1-x.
A las dos últimas filas le restas la primera fila, y queda:
-1 -1 -1
0 2-x 0
0 0 2-x.
Extraes factor común en la primera fila, y queda:
D = (x+1)*(-1)*
1 1 1
0 2-x 0
0 0 2-x.
A las dos últimas columnas le restas la primera columna, y queda:
D = (x+1)*(-1)*
1 0 0
0 2-x 0
0 0 2-x.
Extraes factor común en las dos últimas filas, y queda:
D = (x+1)*(-1)*(2-x)2*
1 0 0
0 1 0
0 0 1.
Resuelves el determinante de la matriz identidad, y queda:
D = (x+1)*(-1)*(2-x)2*1 = -1*(x+1)*(2-x)2 = -1*(x+1)*(x-2)2.
Espero haberte ayudado.pero haberte ayudado.
-
Theo Uni
el 12/6/18
Hola, no me sale este ejercicio de vectores aleatorios, quiero calcular la esperanza de X y de Y, para la esperanza de X iba multiplicando los números de cada fila por la distribución marginal correspondiente y al final lo sumé todo, pero nada que ver con el resultado que me dan. Gracias
Guillem De La Calle Vicente
el 20/6/18Hola! Me encantaría ayudarte, pero no respondemos dudas universitarias que no tengan que ver específicamente con los videos que ya ha grabado como excepcion el profe. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Unicoos llega exclusivamente hasta secundaria y bachillerato
-
Antonio
el 12/6/18Llevo tiempo haciendo operaciones en papel pero no se como despejar esto. Es simple pero no me da:
(1 / X) + (1 / 7,93i) = 0
Osea, (1 entre X) mas (1 entre 7,93i complejo) tiene que ser 0. Tengo que despejar la X.
Antonio Silvio Palmitano
el 12/6/18 -
Javier
el 12/6/18 -
Periko
el 12/6/18Hola buenas, me lío un poco con la diferencia entre ecuación diferencial y solución general.
En este caso, la solución sería una solución general? :
Escribe de la familia de rectas del plano que pasan por el punto (1,2)
Si alguien me echa una mano lo agradecería.
Un saludo
Antonio Silvio Palmitano
el 12/6/18Puedes llamar M a la pendiente genérica de las rectas de la familia, y puedes plantear la ecuación cartesiana punto-pendiente del haz de rectas cuyo centro en el punto A(1,2):
y = M*(x - 1) + 2 (1);
luego, derivas, y queda:
y ' = M;
luego, sustituyes la expresión del primer miembro en la ecuación señalada (1), y queda:
y = y ' * (x -1) + 2,
que es la ecuación diferencial cuyas soluciones son las rectas del haz cuyo centro en el punto A(1,2).
Para verificar, escribes a la expresión de la función derivada como cociente entre diferenciales, y queda:
y = (dy/dx)*(x - 1) + 2, restas 2 en ambos miembros, y queda:
y - 2 = (dy/dx)*(x - 1), separas variables, y queda:
dx/(x-1) = dy/(y-2), integras en ambos miembros, y queda:
ln(x-1) + c = ln(y-2), que es una solución general implícita de la ecuación diferencial;
luego, escribes a la constante c como el logaritmo de otra constante positiva, y queda
ln(x-1) + ln(C) = ln(y-2), aplicas la propiedad del logaritmo de una multiplicación, y queda:
ln( C*(x-1) ) = ln(y-2),
compones en ambos miembros con la función inversa del logaritmo natural, y queda:
C*(x - 1) = y - 2, aquí sumas 2 en ambos miembros, y queda:
C*(x - 1) + 2 = y, lees la ecuación de derecha a izquierda, y queda:
y = C*(x - 1) + 2, que es la solución general explícita de la ecuación diferencial, y observa que es la ecuación del haz de rectas, donde la constante C corresponde a la pendiente M en la ecuación del haz señalada (1).
Espero haberte ayudado.
-
Alejandro Sanchezcarrion
el 12/6/18x asignaturas suspendidas 0 1 2 3 4
f frecuencias 7 3 4 1 5
si elegimos dos alumnos aleatoriamente,calcula la probabilidad de que ambos tengan solo una asignatura suspendida
en la hoja de resultados me pone que el resultado es 3/190 = 0,0157 pero no se como se llega a eso , no debería ser 3/20 por 3/20 ?no se como se llega al 3/190
Antonio Silvio Palmitano
el 12/6/18Puedes plantear dos etapas:
1°)
se elige el primer alumno, y la probabilidad de que tenga una materia suspendida es:
p1 = 3/20;
2°)
se elige el segundo alumno, y la probabilidad de que tenga también tenga una materia suspendida es:
p2 = 2/19.
Luego, por el principio de multiplicación tienes que la probabilidad de elegir dos alumnos con una materia queda:
p = p1 * p2 = (3/20)*(2/19) = 3/190 ≅ 0,015789.
Espero haberte ayudado.
