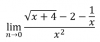-


Antonius Benedictus
el 22/5/18¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
Hola Unicoos, necesito de su ayuda para calcular, por definición, el siguiente límite en dos variables:
lim(x,y) →(-1,1) (3x2 - x.y) = 4
Desde ya muchas gracias!


Antonius Benedictus
el 22/5/18¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-

Jeison
el 21/5/18Si n tiende a cero y la función no tiene n, no tiene sentido. Obviando ese error, y suponiendo que es una errata y pone "x" instead of "n", veamos.
La respuesta es que no existe resultado y te explico. Si te aproximas a cero por la derecha 0+, te da -infinito. Mientras si te aproximas a cero por la izquierda 0-, te da +infinito.
Recuerda que para que exista límite, el límite por la derecha ha de ser igual al limite por la izquierda y en este caso no lo es. Tendrías una asintota donde por un lado se va infinito y por el otro a menos infinito.


Antonio Silvio Palmitano
el 21/5/18Está correcto el procedimiento, pero debes hacer una precisión:
planteas los límites laterales, y queda:
a)
Lím(x→0-) (x*√(x+4) - 2*x -1) / x3 = +∞,
porque el numerador tiende a -1 y el denominador tiende a cero desde valores negativos;
b)
Lím(x→0+) (x*√(x+4) - 2*x -1) / x3 = -∞,
porque el numerador tiende a -1 y el denominador tiende a cero desde valores positivos.
Espero haberte ayudado.
-
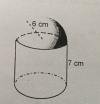
Dadas las líneas xy=4 ; x+y=5 , cañcular el volumen del sólido generado al girar en torno al eje OY la región que encierran.


Antonius Benedictus
el 22/5/18¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
Buenas tardes. En los límites de funciones cuando tengo que seguir una asíntota horizontal (o la línea del x=0), ¿Cómo sé si la flecha va por abajo o por arriba? A veces, en el límite de una función cuando x tiende a infinito, puede servirme sustituir por un número muy grande y según el resultado que me da, sé si la flecha (hacia la derecha o hacia la izquierda) pasa por arriba o por abajo de la asíntota horizontal. Pero muchas veces tengo el ejercicio mal hecho, así que me gustaría saber qué hago mal y/o qué debería hacer para resolver bien el ejercicio y representar bien los límites. Muchas gracias. Indira.

Antonio
el 21/5/18imaginemos que la función tiene una asíntota horizontal en y=6, por lo que el limite cuando x tiende a infinito será 6, y entiendo que quieres saber si la función se aproxima a la misma por arriba o por abajo, pues hay dos formas de saberlo, la primera es, como bien dices, sustituir por un número muy grande y si da 6,algo será por encima y si por el contrario da 5,algo será por abajo; la otra forma es ver si la función decrece (será por arriba) o se crece (será por abajo) en el infinito (o un número muy grande)

Jeison
el 21/5/18Además de lo que comenta Antonio, yo añadiría además que analizaras si la función crece o decrece cuando tiende a infinito. Es decir, si la función crece, es lógico que se acerque por abajo. Por otro lado, si decrece es lógico que se acerca por abajo.
Esto ya sabes que lo puedes hacer derivando la función si es que la tienes. O bien si es el típico problema que te dicen los intervalos de crecimiento y decrecimiento pues, puedes sacarlo por ahí también.
-
Buenas tardes, tengo unas dudas sobre un ejercicio de cálculo diferencial, problema de optimización, si alguien pudiera ayudarme se lo agradecería mucho, el problema dice:
Un minero desea abrir un túnel desde un punto A hasta un punto B situado 80m más abajo que A y 240m al este de él. Debajo del nivel de A es roca; arriba de este nivel es tierra blanda. Si el costo de la construcción del tunel es de $30.00 por metro lineal en tierra y $78 por metro lineal en roca. Hallese el menor costo del túnel.


Antonio Silvio Palmitano
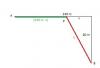
el 21/5/18Puedes llamar (240 m - x) a la longitud de la porción de túnel hecha en tierra (señalada en verde), y puedes llamar z a la longitud de la porción de túnel hecha en roca (señalada en rojo).
Luego, los costos son:
30*(240 - x) para la longitud de la porción hecha en tierra,
78*z para la longitud de la porción hecha en roca;
y la función costo total queda expresada:
C(x,z) = 30*(240 - x) + 78*z, con x > 0 y z > 0.
Luego, puedes plantear el Teorema de Pitágoras en el triángulo de la figura, y queda:
z = √(x2 + 802) = √(x2 + 6400) (1).
Luego, sustituyes la expresión señalada (1) en la expresión de la función costo total, y queda:
C(x) = 30*(240 - x) + 78*√(x2 + 6400), con x > 0.
Luego, planteas la expresión de la función derivada primera, y queda:
C ' (x) = -30 + 78*x/√(x2 + 6400) (2).
Luego, planteas la condición de valor crítico (posible máximo o posible mínimo), y queda:
C ' (x) = 0, sustituyes la expresión de la función derivada señalada (2), y queda:
-30 + 78*x/√(x2 + 6400) = 0, divides por -3 en ambos miembros de la ecuación, y queda:
10 - 26*x/√(x2 + 6400) = 0, sumas 26*x/√(x2 + 6400) en ambos miembros, y queda:
10 = 26*x/√(x2 + 6400), multiplicas por √(x2 + 6400)/2 en ambos miembros, y queda:
5*√(x2 + 6400) = 13*x, elevas al cuadrado en ambos miembros, y queda
25*(x2 + 6400) = 169*x2, distribuyes en el primer miembro, y queda:
25*x2 + 160000 = 169*x2, restas 169*x2 y restas 16000 en ambos miembros, y queda:
-144*x2 = -160000, divides por -144 en ambos miembros, y queda:
x2 = 10000/9,
extraes raíz cuadrada en ambos miembros (observa que elegimos la solución positiva), y queda:
x = 100/3 m ≅ 33,333 m;
luego, evalúas la expresión de la función costo total para el valor remarcado, y queda:
C(100/3) = 30*(240 - 100/3) + 78*√( (100/3)2 + 6400 ) =
= 6200 + 78*√(67600/9) = 6200 + 78*260/3 = 6200 + 20280/3 =
= $ 38880/3 = $ 12960.
Luego, puedes verificar que el valor remarcado corresponde al costo total mínimo si evalúas para valores testigos cercanos al valor crítico, uno menor que él y otro mayor que él:
C(33) = 30*(240 - 33) + 78*√(332 + 6400 ) = 6210 + 78*√(7489) ≅ 6210 + 6750,04 ≅ $ 12960,04,
C(34) = 30*(240 - 34) + 78*√(342 + 6400 ) = 6180 + 78*√(7556) ≅ 6180 + 6780,17 ≅ $ 12960,17;
y puedes apreciar que el costo total mínimo corresponde al valor crítico.
Espero haberte ayudado.