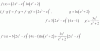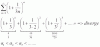Y de alli ya salen tus respuestas ,saludos y no dudes en preguntar

Si no se cortan entonces creo que sería la distancia entre sus dos vértices.

No entiendo tu pregunta miráte esto

http://www4.ujaen.es/~angelcid/Archivos/An_Mat_ESTADISTICA/Apuntes/T2_Sucesiones_Series.pdf

creo que este es

https://www.youtube.com/watch?v=jCDxBLS351I&start_radio=1&list=RDjCDxBLS351I

Evalúas la expresión de la función para la abscisa del punto de contacto, y tienes:

h(1) = 1, que es la ordenada de dicho punto, que queda expresado: A(1,1).

Luego, planteas la expresión de la función derivada, y queda: h ' (x) = -1/x², 

luego evalúas esta expresión para la abscisa del punto de contacto, y queda: h ' (1) = -1,

que es el valor de la pendiente de la recta tangente en el punto de contacto, que queda expresada:

m = 1.

Luego, con las coordenadas del punto de contacto y con el valor de la pendiente, puedes plantear la ecuación punto pendiente de la recta tangente a la gráfica de la función en el punto A:

y = m*(x - x_A) + y_A, 

reemplazas valores, y queda:

y = -1*(x - 1) + 1,

distribuyes el primer término, reduces términos numéricos, y queda:

y = -x + 2,

que es la ecuación cartesiana explícita de la recta tangente a la gráfica de la función en el punto A.

Espero haberte ayudado.

Tienes la expresión numérica:

x = -5 / √(5),

multiplicas al numerador y al denominador por √(5), y queda

x = -5*√(5) / √(5)*√(5),

escribes al denominador como una potencia, y queda:

x = -5*√(5) / ( √(5) )², 

simplificas raíz y potencia en el denominador, y queda:

x = -5*√(5) / 5,

simplificas, y queda:

x = -√(5).

Espero haberte ayudado.