-
César
el 23/5/18Iván
el 23/5/18Yo la dejaría expresada. Al ser un trapecio isósceles sabes que ambos triángulos son iguales, y por ende sus bases.
Llamando "x" a la base que forma los dos triángulos y "z" a la base de lo que sería el rectángulo te queda algo así: 2x+z=14
De aquí despejas z, lo que equivale a la base superior del trapecio: z=14-2x
Sabiendo la fórmula del área del trapecio se podría dejar el área expresada de esta manera: A=(B+b)*h/2 >>> B=14 b=z=14-2x >>> A=(14+14-2x)*h/2 >>> A= (28h - 2xh)/2 >>> A= 14h - xh
-
Buenas tardes,
Solo se trataba para saber si el libro esta errado en donde o he subrayado en rojo. ¿Al sustituir la antitransformada no debería de ser e-u?
Ya se que es un tema universitario pero la duda solo la tengo al sustituir los términos en la integral. Por cierto f(t)=et
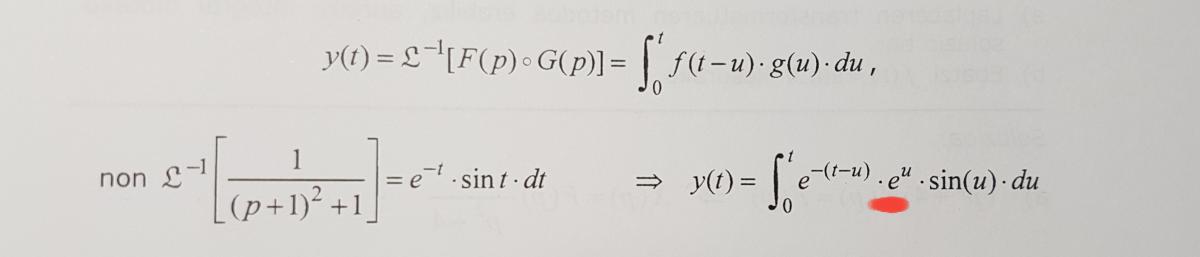
-
Antonius Benedictus
el 23/5/18¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
Buen día UNICOOS... me puede ayudar con unas dudas que me han surgido.
1.- ¿Es lo mismo "Interpolación Lineal"que una "Regresión Lineal"?
2.- ¿Si se tienen dos pares de conjuntos con valores, xq para los valores de x siempre se toman valores de igual longitud (de 10 en 10)?
108
205.45304.01403.98501.01Se me ocurren esos valores...
En si quiero saber que es una interpolación Lineal y para que me sirve, de igual manera con la interpolación.
Si alguien me puede despejar de esta duda se lo agradezco infinitamente xq tengo tareas de mi carrera, y usamos esto como requisito, y no lo domino bien por esto.
Guillem De La Calle Vicente
el 23/5/18La principal diferencia entre interpolación y regresión, es la definición del problema que resuelven.
Dados n puntos de datos, al interpolar, se busca una función que sea de alguna forma predefinida que tenga los valores en esos puntos exactamente como se especificó. Esto significa que los pares dados (xi, yi) buscan F de alguna forma predefinida que satisfaga F(xi)=yi. Creo que lo más común es que F sea un polinomio de bajo grado en intervalos entre puntos dados.
Cuando se realiza una regresión, se busca una función que minimice algún costo, generalmente la suma de cuadrados de errores. No se requiere que la función tenga los valores exactos en puntos dados, sólo se desea una buena aproximación. En general, es posible que la función F encontrada no satisfaga F(xi)=yi para cualquier punto de datos, pero la función de coste, es decir ∑i=1n(F(xi)-i)2 será la más pequeña posible de todas las funciones de un formulario dado.
Un buen ejemplo de por qué es mejor aproximar en lugar de interpolar son los precios en el mercado de valores. Puedes tomar los precios en algunos k unidades de tiempo recientes, y tratar de interpolarlas para obtener alguna predicción del precio en la siguiente unidad de tiempo. Esto es más bien una mala idea, porque no hay razón para pensar que las relaciones entre los precios pueden ser expresadas exactamente por un polinomio. Pero la regresión lineal podría funcionar muy bien, ya que los precios podrían tener alguna "pendiente" y una función lineal podría ser una buena aproximación, al menor localmente. No es tan fácil, pero la regresión es definitivamente una mejor idea que la interpolación en este caso.
Saludos.
-
Javier Suárez Caballero
el 23/5/18Se trata de un problema de probabilidad total. Haz un diagrama en árbol:
En total hay 13 caramelos y el experimento es sin reemplazamiento.
P (Fresa) = 8/13 P (Limón) = 5/13
Como se extrae un segundo caramelo, ahora los casos posibles son 12...
Ahí te dejo el planteamiento. Síguelo tú ;)