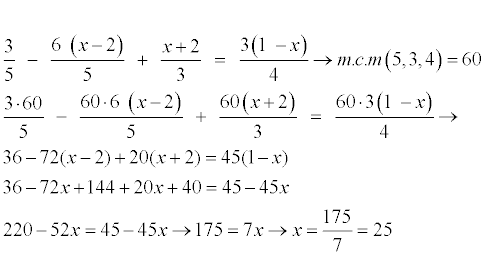Razones trigonométricas

(k-1,k+2)·(3,7)=31

(k-1)3+(k+2)7=31

3k-3+7k+14=31

10k=31-11

10k=20

k=2

Explicate un poco mejor 

https://es.wikipedia.org/wiki/Distribuci%C3%B3n_hipergeom%C3%A9trica

a)

Observa que la extracción de un balón rojo en una instancia influye sobre las instancias siguientes, ya que la probabilidad de extraer un balón rojo se modifica, y tienes que las extracciones no son independientes.

a₁)

Observa que tienes una variable aleatoria discreta cuyos valores posibles son: 0, 1, 2, 3.

Luego, sus probabilidades son: 

p(X=0) = p(BBB) = (4/10)(3/9)(2/8) = 1/30,

p(X=1) = p(RBB) +  p(BRB) + p(BBR) = (6/10)(4/9)(3/8) + (4/10)(6/9)(3/8) + (4/10)(3/9)(6/8) = 3/10,

p(X=2) = p(RRB) + p(RBR) + p(BRR) = (6/10)(5/9)(4/8) + (6/10)(4/9)(5/8) + (4/10)(6/9)(5/8) = 1/2,

p(X=3) = p(RRR) = (6/10)(5/9)(4/8) = 1/6.

a₂)

Observa que el suceso "se eligen dos balones blancos en la extracción" coincide con el suceso "se elige un balón rojo en la extracción", por lo que su probabilidad es

P(X=1) = 3/10.

a₃)

p(-2<X≤3) = p(X=0) + p(X=1) + p(X=2) + p(X=3) = 1/30 + 3/10 + 1/2 + 1/6 = 1.

a₄)

p(X>2) = p(X=3) = 1/6.

b)

Observa que la extracción de un balón rojo en una instancia no influye sobre las instancias siguientes, ya que la probabilidad de extraer un balón rojo permanece constante, y tienes que las extracciones son independientes.

b₁)

Observa que tienes una variable aleatoria discreta con distribución binomial, cuyos valores posibles son: 0, 1, 2, 3, 4, 5, 6, 7, 8, y cuyos parámetros son:

n = 8, p = 6/10 = 0,6, con la probabilidad complementaria: q = 1 - p = 0,4.

Luego, la expresión de la función de distribución de probabilidad es:

p(X=k) = C(n,k)*p^k*q^n-k, reemplazas valores, y queda:

p(X=k) = C(8,k)*0,6^k*0,4^8-k.

b₂)

p(X≥2) = 1 - p(X<2) = 1 - ( p(X=0) + p(X=1) ) = 1 - p(X=0) - p(X=1),

sustituyes expresiones, y queda:

p(X≥2) = 1 - C(8,0)*0,6⁰*0,4^8-0 - C(8,1)*0,6¹*0,4^8-1 = 

= 1 - 1*1*0,4⁸ - 8*0,6*0,4⁷ =

= 1 - 0,00065536 - 0,00786432 = 0,99148032.

b₃)

μ = E(X) = n*p, reemplazas valores, y queda:

μ = E(X) = 8*0,6 = 4,8,

por lo que puedes considerar que la cantidad promedio de balones rojos a extraer es aproximadamente igual a cinco.

Espero haberte ayudado.

La solución es 47, lo saqué a base de probar y probar.

me explico:

La pareja 412 y 365 es la que da esa solución, por lo que tendrá que ser esa o 38.

y cualquier otra no da 38, por lo que güalá, ya la tienes.

Puedes plantear los desarrollos de los números en potencias de diez:

x = 100a + 10b + c,

y = 100d + 10e + f,

donde a, b, c, d, e, f pueden tomar los valores: 1, 2, 3, 4, 5, 6.

Luego, plantea la expresión de la resta entre los números:

x - y = ( 100a+10b+c ) - ( 100d+10e+f ),

distribuyes agrupamientos, extraes factores comunes y asocias términos, y queda:

x - y = 100(a-d) + 10(b-e) + (c-f).

Luego, puedes plantear que la diferencia (a-d) es mínima, por lo tanto tienes:

a - d = 1.

Luego, puedes plantear que la diferencia (b-e) es negativa y lo más grande posible en valor absoluto, a fin de afectar a las cifras de las centenas en la resta, por lo tanto tienes:

b - e < 0.

Luego, puedes plantear que la diferencia (c-f) es negativa y lo más grande posible en valor absoluto, a fin de afectar a las cifras de las decenas en la resta, por lo tanto tienes:

c - f < 0.

Con todas estas consideraciones, observa que debes elegir a las cifras a y d de tal forma que sean lo más cercanas posibles, con a mayor que d; y a las cifras b y e lo más lejanas posibles, con b menor que e; y a las cifras c y f lo más lejanas posibles, con c menor que f.

Luego, puedes elegir:

a = 4 y d = 3.

Luego, puedes elegir:

b = 1 y e = 6.

Luego, puedes elegir:

c = 2 y f = 5.

Luego, los números quedan:

x = 412,

y = 365;

y observa que su diferencia es:

x - y = 47.

Espero haberte ayudado.

Si es antisimétrica para todo x, y se verifica xRy ∧ yRx → x=y

Si es no-simétrica existen alguno x,y tal que xRy ∧ y∼Rx

Por ejemplo en el conjunto A = {1,2} la relación R ={(1,1) (2,2)} es antisimétrica pero no es no-simétrica? 

Rectifico:

Es simétrica, pues:

Si xRy, entonces yRx.

Es antisimétrica, pues xRy, yRx implica x=y.

La antisimetría no es lo opuesto de la simetría.

Existen relaciones que son simétricas y antisimétricas al mismo tiempo (como la igualdad), otras que no son simétricas ni antisimétricas (como la divisibilidad para los enteros), otras que son simétricas pero no antisimétricas (como la relación de congruencia módulo n), y otras que son antisimétricas pero no simétricas (como la relación "menor que").

¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que  lo entiendas.

Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).

Observa que la superficie es un casquete esférico con eje de simetría OZ, y cuya proyección sobre el plano OXY es un disco circular con centro en el origen de coordenadas y cuyo radio es igual a 4.

Luego, puedes proponer una parametrización "con estilo coordenadas cilíndricas" para la superficie:

x = u*cosv,

y = u*senv,

z = √(25-u²),

con el recinto paramétrico (R):

0≤u≤4,

0≤v≤2π.

Luego, planteas la expresión de la función vectorial de posición, y queda:

R(u,v) = <u*cosv,u*senv,√(25-u²)>, con el recinto paramétrico que ya tienes consignado.

Luego, planteas las expresiones de las funciones derivadas parciales, y quedan:

R_u(u,v) = <cosv,senv,-u/√(25-u²)>,

R_v(u,v) = <-u*senv,u*cosv,0>.

Luego, planteas al producto vectorial entre las dos últimas expresiones como un vector normal a la superficie en todos sus puntos, y queda:

N(u,v) = R_u(u,v) x R_v(u,v) = <u²*cosv/√(25-u²),u²*senv/√(25-u²),u> (1).

Luego, tienes la expresión del campo vectorial (observa que tiene componentes continuas con derivadas parciales primeras continuas en R³):

F(x,y,z) = <xz,yz,1>;

sustituyes las expresiones de x, y, z en función de los parámetros u, v, y queda:

F(R(u,v)) = <u*cosv*√(25-u²),u*senv*√(25-u²),1> (2).

Luego, planteas el producto escalar entre la expresión del campo vectorial y la expresión del vector normal, y queda:

F(R(u,v)) • N(u,v) =

sustituyes las expresiones señaladas (2) (1), y queda:

= <u*cosv*√(25-u²),u*senv*√(25-u²),1> • <u²*cosv/√(25-u²),u²*senv/√(25-u²),u> = 

desarrollas el producto escalar, y queda:

= u³*cos²v + u³*sen²v + u = 

extraes factor común en los dos primeros términos, y queda:

= u³*(cos²v + sen²v) + u = 

aplicas la identidad trigonométrica fundamental en el primer término, resuelves, y queda:

= u³ + u (3).

Luego, puedes plantear la integral de flujo del campo vectorial F a través de la superficie S:

Φ_F = ∫∫_S F(x,y,z) • dS =

planteas el desarrollo de la integral de superficie en función de la parametrización, y queda:

= ∫∫_R F(R(u,v)) • (N(u,v)/|N(u,v)|)*|N(u,v)|*du*dv =

simplificas factor y divisor, y queda:

= ∫∫_R F(R(u,v)) • (N(u,v) * du*dv =

sustituyes la expresión señalada (3), consignas los límites de integración, y queda:

= ₀∫^2π₀∫⁴ (u³ + u)*du*dv = y puedes continuar la tarea.

Espero haberte ayudado.