-
Buenas, alguien me podria explicar como pasar la ecuacion general de un plano, a la ecuacion parametrica del plano?
Javier Suárez Caballero
el 23/5/18Hola, Ale:
Si tienes la ecuación general Ax + By + C = 0 y quieres obtener las ecuaciones paramétricas, lo único que necesitas es un vector director.
¿Cómo lo obtienes? Muy sencillo...
Imagina que tienes la recta 4x + 3y - 3 = 0. Tan solo debes sacar dos puntos que contienen a la recta dando valores. Por ejemplo:
Si x = 0 --> y = 1 (0, 1)
Si x = 1 --> y = -1/3 (1, -1/3)
Una vez hallados dos puntos, el vector director se calcula así: ( 1 - 0, -1/3 - 1), es decir, restando el extremo menos el origen.
Al determinar el vector director, simplemente elige un punto cualquiera y obtén las paramétricas.
Espero te haya servido. Un abrazo!!
-
Es igual de exacto el valor de una pendiente mediante regresión lineal con 2 que con 4 puntos?
Guillem De La Calle Vicente
el 23/5/18Depende del modelo para los datos y el ruido en las mediciones.
Si no tienes absolutamente ningún ruido, entonces obtendrás la misma respuesta con regresión lineal si usas 2 o 4 puntos.
Si hay ruido pero los datos realmente siguen un modelo lineal, entonces (en términos generales) cuantos más puntos tenga, mejor será su estimación.
saludos.
-
Buenas noches
Alguien me podría recordar en que funciones era neceario realizar la comprobación de las soluciones???
lineales,polinomicas,bicuadradas,racionales,irracionales,exponenciales...
GRACIAS.
-
Usuario eliminado
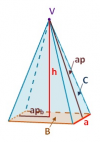
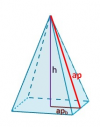
el 22/5/18Entonces tenemos que la arista mide 10 mm y tiene una altura de 5mm
Necesitamos hallar la apotema de la base ,para ello como sabemos la altura y también sabemos la longitud de la arista ,habremos de aplicar Pitágoras,ya que forman un triángulo rectángulo
apb es 5 mm puesto que cojemos solo la mitad para a hacer el cálculo.
Ap2=h2+apb2
Ap2=52 +52
Ap=7,071mm
Entonces ahora vamos con el área de la base
Sabemos que es un cuadrado y el área de este es
AB =c2
AB =102
AB=100 mm
Ahora el Área Lateral
Al=Pb*Ap ⁄ 2
Al=10*4*7,071/2
Al=141,42 mm
Y el área total
At=AB + Al
At=100+141,42
At=241,42 mm
Para el volumen usamos esta fórmula
V=AB *h/ 3
V=100 *5/3
V=166,66 mm3
Espero haberte ayudado
-
Antonius Benedictus
el 22/5/18Antonio Silvio Palmitano
el 22/5/18Observa que puedes dividir la figura en dos figuras simples:
1)
Un semicículo cuyo radio mide x/2, y cuya área queda expresada:
A1 = (1/2)*π*(x/2)2 = (1/2)*π*x2/4 = (1/8)*π*x2;
2)
Un rectángulo cuya base mide x y cuya altura mide y, y cuya área queda expresada:
A2 = x*y.
Luego, tienes que el área total es la suma de las áreas de las dos figuras simples, por lo que tienes:
f(x,y) = A1 + A2, sustituyes expresiones, y queda:
f(x,y) = (1/8)*π*x2 + x*y.
Luego, plantea la expresión del perímetro de la figura (observa que comprende una base, dos alturas y una semicircunferencia cuyo radio mide x/2, por lo que su expresión queda:
P(x,y) = x + 2*y + (1/2)*π*x.
Luego, tienes en tu enunciado que el perímetro de la figura es 20 m, por lo que puedes plantear la ecuación:
P(x,y) = 20 m, sustituyes la expresión del perímetro en el primer miembro, y queda:
x + 2*y + (1/2)*π*x = 20, restas x y restas (1/2)*π*x en ambos miembros de la ecuación, y queda:
2*y = 20 - x - (1/2)*π*x, multiplicas por 1/2 en todos los términos de la ecuación, y queda:
y = 10 - (1/2)*x - (1/4)*π*x (1).
Luego, sustituyes la expresión señalada (1) en la expresión de la función que tienes remarcada, y queda:
f(x) = (1/8)*π*x2 + x*(10 - (1/2)*x - (1/4)*π*x), distribuyes el último término, y queda:
f(x) = (1/8)*π*x2 + 10*x - (1/2)*x2 - (1/4)*π*x2 (2).
Luego, planteas la expresión de la función derivada primera, y queda:
f ' (x) = (1/4)*π*x + 10 - x - (1/2)*π*x (3).
Luego, planteas la expresión de la función derivada segunda, y queda:
f ' ' (x) = (1/4)*π - 1 - (1/2)*π = -(1/4)*π - 1 (4).
Luego, planteas la condición de valor crítico (posible máximo o posible mínimo), y queda:
f ' (x) = 0, sustituyes la expresión señalada (3) en el primer miembro, y queda:
(1/4)*π*x + 10 - x - (1/2)*π*x = 0, restas 10 en ambos miembros, y queda:
(1/4)*π*x - x - (1/2)*π*x = -10, multiplicas por -4 en todos los términos de la ecuación, y queda:
-π*x + 4*x + 2*π*x = 40, extraes factor común en el primer miembro, y queda:
x*(-π + 4 + 2*π) = 40, reduces términos irracionales en el agrupamiento, y queda:
x*(π + 4) = 40, divides por (π + 4) en ambos miembros, y queda:
x = 40/(π + 4) m ≅ 5,601 m.
Luego, evalúas este último valor remarcado en la expresión de la función derivada segunda señalada (4), y queda:
f ' ' ( 40/(π + 4) ) = -(1/4)*π - 1 < 0,
por lo que tienes que la gráfica de la función área es cóncava hacia abajo en el valor crítico, por lo que puedes concluir que la gráfica de la función presenta un máximo para dicho valor.
Luego, evalúas la expresión de la función señalada (2) para el valor crítico, y tendrás el valor del área máxima (te dejo la tarea).
Espero haberte ayudado.
-
Necesito ayuda con esto. Formé vectores con los puntos restando p2-p1, p3-p2 y p3-p1. Después establecí un vector AB y AC restando sus componentes (resté las primeras componentes del segundo vector o sea b-a y c-a). Al final realicé el producto vectorial pero me da -14x,-14y,+28z (xyz=ijk).
Me explicarían que hice mal? GRACIAS, MAÑANA ES MI PARCIAL.
Guillem De La Calle Vicente
el 22/5/18¿Cómo se define un vector para ser perpendicular... a un área?
¿Cuáles son los componentes de p2 - p1 y p3 - p1? ¿Cuál es el producto vectorial de estos vectores? No nos muestras todos tus pasos, así que no podemos decirle dónde comete el error. Tal vez calculó mal los vectores. O tal vez el producto vectorial.
Saludos.
Antonio Silvio Palmitano
el 22/5/18A partir de la imagen tienes las coordenadas de los tres vértices del triángulo:
P1(1,1,0), P2(4,6,0), P3(0,4,2).
Luego, plantea las expresiones de dos vectores (elegimos al primer punto como punto de aplicación en común para los dos vectores):
u = P1P2 = < 4-1 , 6-1 , 0-0 > = < 3 , 5 , 0 >,
v = P1P3 = < 0-1 , 4-1 , 2-0 > = < -1 , 3 , 2 >.
Luego, puedes proponer al producto vectorial entre los dos vectores como un vector perpendicular al plano determinado por los tres vértices del triángulo (y, por lo tanto, perpendicular al triángulo):
p = u x v = < 3 , 5 , 0 > x < -1 , 3 , 2 > = < 10 , -6 , 14 >.
Luego, recuerda que cualquier vector que sea múltiplo escalar no nulo del vector p también será un vector perpendicular a la superficie.
Espero haberte ayudado.