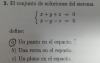-
Buenos días, tengo unas dudas sobre unos ejercicios de álgebra de 1º de carrera en ingeniería. Si alguien pudiera ayudarme lo agradecería mucho!
Muchas gracias.
Antonius Benedictus
el 21/5/18¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
---------------DERIVADA---------------
Indicar si existen los puntos donde cada una de las gráficas de las siguientes funciones tienen tangente horizontal y tangente vertical.
a)f(x)=x^2-3x+2
Ayuda, lo que necesito es teoría para resolver el ejercicio, encontré como sacar la tangente horizontal que es igualando la pendiente de la recta tangente a 0, pero no encuentro como sacar la tangente vertical.
Antonius Benedictus
el 21/5/18Jonathan Yañez
el 21/5/18Para formalizar un poco el concepto, esto estaría bien?
Para encontrar la tangente vertical primero debo hallar la derivada, luego encontrar las raíces del denominador, las cuales harán que la pendiente de la recta tangente valga infinito cuando las introduzca en la función. Se debe verificar los limites por izquierda y por derecha, ya que el resultado en ambos debe ser infinito o - infinito, ya que se obtengo infinitos con distinto signo es un punto cuspidal y no una tangente vertical.
-
asi se ve mejor, gracias a quien pueda ayudarme

Antonio Silvio Palmitano
el 21/5/18Tienes la ecuación logarítmica:
loga(x) = 3*( loga(5) + 4*loga(2) - loga(3) ).
Aplicas la propiedad del logaritmo de una potencia en el segundo término del agrupamiento, y queda:
loga(x) = 3*( loga(5) + loga(24) - loga(3) ).
Resuelves el argumento del logaritmo en el segundo término del agrupamiento, y queda:
loga(x) = 3*( loga(5) + loga(16) - loga(3) ).
Aplicas la propiedad del logaritmo de una multiplicación, y la propiedad del logaritmo de una división, en el agrupamiento, y queda:
loga(x) = 3*loga(5*16/3).
Resuelves el argumento del logaritmo en el segundo miembro, y queda:
loga(x) = 3*loga(80/3).
Aplicas la propiedad del logaritmo de una potencia en el segundo miembro, y queda:
loga(x) = loga( (80/3)3).
Resuelves el argumento del logaritmo en el segundo miembro, y queda:
loga(x) = loga( 512000 / 27 ).
Compones en ambos miembros con la función inversa del logaritmo en base a, y queda:
x = 512000 / 27.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 21/5/181)
Observa que tienes un límite indeterminado, ya que tanto el numerador como el denominador tienden a cero cuando x tiende a cero.
Aplicas la Regla de L'Hôpital (derivas independientemente al numerador y al denominador), y queda:
L = Lím(x→0) (1*senx + x*cosx) / ( 2x/(1+x2) );
resuelves la división entre expresiones en el argumento, y queda:
L = Lím(x→0) ( (1+x2)*(senx + x*cosx) ) / (2x);
aplicas la Regla de L'Hôpital (derivas independientemente al numerador y al denominador), y queda:
L = Lím(x→0) ( 2x*(senx + x*cosx) + (1+x2)*(cosx + 1*cosx - x*senx) ) / 2;
resuelves y queda (observa que el numerador tiende a dos y que el denominador es igual a dos):
L = 1.
Espero haberte ayudado.
-
 Buenas tardes únicos. Por qué la indeterminación es 0/0? Gracias
Buenas tardes únicos. Por qué la indeterminación es 0/0? Gracias
-
Sea el experimento que consiste en lanzar una moneda al aire. Si sale cara acudimos a la urna A cuya composición es: 4 bolas azules, 3 rojas y 3 verdes, y extraemos una bola; si sale cruz, vamos a la urna B compuesta por: 5 A, 2 R y 3 V y, nuevamente extraemos una bola. Hallar: a) El espacio muestral del suceso compuesto. b) Hallar la probabilidad de cada uno de los sucesos del espacio muestral. c) Probabilidad de obtener bola roja. d) Probabilidad de que sabiendo que la bola extraída es roja, pertenezca a la urna B.
Antonio
el 21/5/18 -
Antonius Benedictus
el 21/5/18¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).