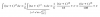Hola Sandra. 

Lo tienes resuelto más abajo, en tu publicación anterior.

¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que  lo entiendas.

Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).

Observa que la función es continua en el valor en estudio.

Observa que el valor en estudio es x₀ = 1, que es el que corresponde al corte entre los dos trozos de la función, por lo que debes plantear las derivadas laterales por medio de la definición.

Luego, plantea la derivada lateral izquierda (observa que la función toma el valor: f(1) = 1²+3 = 4 en el valor en estudio: x₀ = 1):

f_-' (1) = Lím(h→0-) ( f(1+h) - f(1) )/h = 

reemplazas el valor de la función en el segundo término del numerador, y queda:

= Lím(h→0-) ( f(1+h) - 4 )/h = 

sustituyes la expresión del primer término en el numerador (observa que debes emplear la expresión de la primera rama), y queda:

= Lím(h→0-) ( (1+h)²+3 - 4 )/h = 

desarrollas el binomio elevado al cuadrado en el primer término del numerador, y queda:

= Lím(h→0-) (1+2h+h² + 3 - 4)/h =

reduces términos numéricos (observa que tienes una cancelación), y queda:

= Lím(h→0-) (2h+h²)/h =

extraes factor común en el numerador, y queda:

= Lím(h→0-) h(2+h)/h =

simplificas, y queda:

= Lím(h→0-) (2+h) = 2 (1).

Luego, plantea la derivada lateral derecha (observa que la función toma el valor: f(1) = 1²+3 = 4 en el valor en estudio: x₀ = 1):

f₊' (1) = Lím(h→0+) ( f(1+h) - f(1) )/h = 

reemplazas el valor de la función en el segundo término del numerador, y queda:

= Lím(h→0+) ( f(1+h) - 4 )/h = 

sustituyes la expresión del primer término en el numerador (observa que debes emplear la expresión de la segunda rama), y queda:

= Lím(h→0+) ( 4+ln(1+h) - 4 )/h = 

reduces términos numéricos (observa que tienes una cancelación), y queda:

= Lím(h→0+) ln(1+h)/h =

expresas al argumento del límite como una multiplicación, y queda:

= Lím(h→0+) (1/h)*ln(1+h) =

aplicas la propiedad del logaritmo de una potencia, y queda:

= Lím(h→0+) ln( (1+h)^1/h ) = 

aplicas la propiedad del límite de una función logarítmica, y queda:

= ln( Lím(h→0+) (1+h)^1/h ) = 

luego, observa que tienes la expresión de un límite trascendente en el argumento del logaritmo (revisa tus apuntes de clase), cuyo valor es el número irracional trascendente e, por lo que reemplazas su valor, y queda:

= ln( e ) = 1 (2).

Luego, como los valores remarcados y señalados (1) (2) son distintos, entonces tienes que las derivadas laterales calculadas en el valor en estudio x₀ = 1 no coinciden, por lo que puedes concluir que la función derivada no está definida para este valor.

Luego, la expresión de la función derivada queda (observa que aplicamos reglas de derivación en las expresiones de las ramas):

f ' (x) =

2x                               si x < 1

no está definida      si x = 1

1/x                             si x > 1.

Espero haberte ayudado.

Como integral inmediata que es:

3x^2 + x +C

i si fuese elevado a algo? ya no sería inmediata?

quiero decir... ∫ (6x+1)ⁿ dx

siendo n un numero, 4 o 5 por ejemplo. 

Únicamente tienes hallar los vectores directores de r y s y realizar su producto mixto (i,j,k) que será el vector director de tu nueva recta t.

Hallar la intersección de r y s (pto P). Dados un vector director y un pto p podrás construir tu recta t

Creo...

¿Alguien sabe por que no me dejan hacer preguntas en el foro?

Solo me deja responder

Ah!!! y lo ultimo ¿Para que te den las medallas tienes que ser pro por que a mi no me pone ninguna y tendría que tener alguna?

Hola no te dejan hacer preguntas porque no has evaluado las respuestas que te han dado 

Gracias tio

Y lo de las medallas lo sabes???

No.

Con la Regla de Laplace:
Nº de casos favorables entre nº de casos posibles.

y por qué el 1-? si la formula no tiene eso.

La probabilidad del contrario de un suceso dado es 1 menos la probabilidad de dicho suceso.

Posición relativa de rectas y planos

No me deja ver los videos de la posición relativaa para poder entender el ejercicio