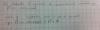-
¡¡¡URGENTE!!!
Tengo un examen el lunes que viene y no consigo resolver este ejercicio. Dice lo siguiente:
La figura siguiente representa la región solución de un sistema de inecuaciones lineales:
a) Encuentra el sistema de inecuaciones que determina la región solución.
b) Encuentra el valor de a para que la función f(x,y) = ax+2y+3 tenga un máximo en el segmento comprendido entre los extremos (4,2) y (5,0)
¡Gracias!
Sebastian Quintero
el 10/5/18 -
Gracia Rández
el 10/5/18 -
Antonio Silvio Palmitano
el 10/5/18Recuerda las identidades correspondientes a la composición de la función logarítmica natural con su función inversa:
elnu = u, con u > 0, y ln(eu) = u, con u ∈ R.
Luego, a partir de la identidad remarcada, tienes:
eln2 = 2 (1).
Luego, tienes la expresión evaluada de la derivada parcial con respecto a x de la función:
fx(1,ln2) =
= eln2*(2*ln2) + eln2 =
reemplazas el valor señalado (1) en los factores remarcados, y queda:, y queda:
= 2*(2*ln2) + 2 =
resuelves el primer término, y queda:
= 4*ln2 + 2.
Espero haberte ayudado.
-
-
Hola buenas tardes me podrian ayudar con estos ejercicios de derivadas no los entiendo seria desde el ejercicio 2 hasta el 5 con este tema de derivadas estoy muy perdido gracias
-