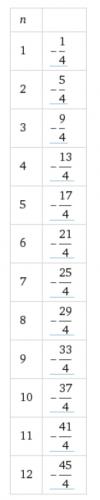
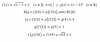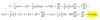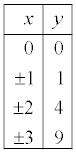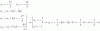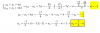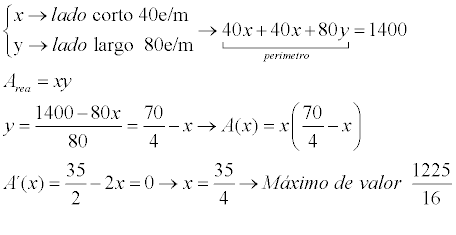-
Antonio Silvio Palmitano
el 9/5/18Puedes plantear la ecuación cartesiana explícita de la recta tangente (indicamos con b a la ordenada al origen):
y = 2x + b (1).
Luego, sustituyes la expresión señalada (1) en la ecuación de la elipse, y queda:
9x2 + 4(2x + b)2 + 108x + 40(2x + b) + 388 = 0,
desarrollas el segundo y el cuarto termino, y queda:
9x2 + 16x2 + 16bx + 4b2 + 108x + 80x + 40b + 388 = 0,
reduces y asocias términos según la incógnita x, y queda:
25x2 + (16b + 188)x + (4b2 + 40b + 388) = 0,
que es una ecuación polinómica cuadrática, cuyos coeficientes son:
A = 25, B = 16b + 188, C = 4b2 + 40b + 388,
y cuyo discriminante: D = B2 - 4AC, observa que debe ser igual a cero para tener un único punto de intersección entre la recta tangente y la elipse, por lo que puedes plantear la ecuación:
B2 - 4AC = 0, sustituyes las expresiones de los coeficientes, y queda:
(16b + 188)2 - 4(25)(4b2 + 40b + 38)8 = 0,
desarrollas los dos términos, y queda:
256b2 + 6016b + 35344 - 400b2 - 4000b -38800 = 0,
reduces términos semejantes, y queda:
-144b2 + 2016b - 3456 = 0,
divides en todos los términos de la ecuación por -144, y queda:
b2 - 14b + 24 = 0,
que es una ecuación polinómica cuadrática, cuyas soluciones son:
a)
b = 2,
reemplazas en la ecuación de la recta tangente señalada (1), y queda:
y = 2x + 2;
b)
b = 12,
reemplazas en la ecuación de la recta tangente señalada (1), y queda:
y = 2x + 12.
Luego, tienes las ecuaciones de las dos rectas tangentes a la elipse, con pendiente igual a dos para ambas rectas.
Luego (te dejo la tarea), puedes plantear dos sistemas de ecuaciones, con la ecuación de la elipse en ambos sistemas, y la ecuación de cada una de las rectas, para determinar las coordenadas del punto de contacto de cada recta con la elipse
Espero haberte ayudado.
-
Holaa David, acabo de terminar de ver tu video. ¿Cómo se representaria graficamente la funcion y=2x² ?
Es que no acabo de entenderlo, gracias.
Lucía
el 9/5/18