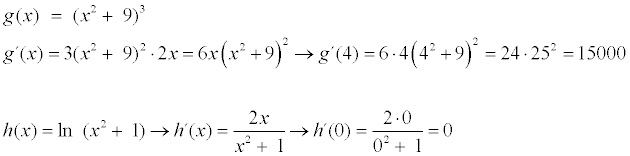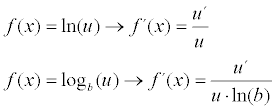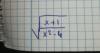Enviale un correo:

unicoos@unicoos.com

Saludos.

Gracias por su respuesta! Una cosita, en el examen no aparece "ln" sino "L" por lo que he creído que era un logaritmo en base 10. Siempre que me pongan una L mayúscula se refieren a ln? y en el caso de que hubiera sido en base 10 habría estado bien mi solución? Gracias de nuevo :)

En general al logaritmo en base 10 se le suele denominar  log

mientras que al neperiano se le suele denominar ln   o   L, esta última es menos usual.

También es  correcto.

Considera la variable aleatoria:

X: "cantidad de alumnos de la muestra que desaprueba el consumo de marihuana".

Observa que la variable tiene distribución normal con parámetros: n = 7, p = 0,7,

con la probabilidad complementaria: q = 1 - p = 0,3,

y observa que la variable puede tomar valores naturales con 0 como mínimo y 7 como máximo.

Luego, la expresión de la función de distribución es:

p(X = k) = C(7,k)*0,7^k*0,3^7-k.

a)

p(5 ≤ X ≤ 7) =

= p(X = 5) + p(X = 6) + p(X = 7) =

= C(7,5)*0,7⁵*0,3² + C(7,6)*0,7⁶*0,3¹ + C(7,7)*0,7⁷*0,3⁰ =

= 0,3176523 + 0,2470629 + 0,0823543 =

= 0,6470695.

b)

p(X ≤ 5) =

= 1 - p(X > 5) =

= 1 - ( p(X = 6) + p(X = 7) ) =

= 1 - p(X = 6) - p(X = 7) =

= 1 - 0,2470629 - 0,0823543 =

= 0,6705828.

c)

p(X ≥ 4) = 

= p(X = 4) + p(X = 5) + p(X = 6) + p(X = 7) =

= C(7,4)*0,7⁴*0,3³ + C(7,5)*0,7⁵*0,3² + C(7,6)*0,7⁶*0,3¹ + C(7,7)*0,7⁷*0,3⁰ =

= 0,2268945 + 0,3176523 + 0,2470629 + 0,0823543 =

= 0,873964.

d)

μ = n*p = 7*0,7 = 4,9 (media);

σ² = n*p*q = 7*0,7*0,3 = 1,47 (varianza);

σ = √(n*p*q) = √(1,47) ≅ 1,212436 (desviación típica).

Espero haberte ayudado.

Tienes las probabilidades de elegir una caja es la misma para las tres cajas:

p(V) = p(R) = p(A) = 1/3.

Luego, si llamas x a la probabilidad de sacar cruz con la moneda de la caja verde, entonces tienes que la probaibilidad de sacar cara con dicha moneda es 2x, y luego puedes plantear.

x + 2x = 1, reduces términos semejantes, y queda: 3x = 1, divides por 3 en ambos miembros, y queda: x = 1/3,

de donde tienes que la probabilidad de sacar cruz con la moneda de la caja roja es 1/3, y la probabilidad de sacar cara es 2/3.

Luego, considera la probablidad condicional de sacar cara sabiendo la caja de la que proviene la moneda:

p(C|V) = 2/3, p(C|R) = 1, p(C|A) = 1/2.

Luego, puedes plantear para la probabilidad del suceso "salió cara":

p(C) =

= p(C∩V) + p(C∩R) + p(C∩A) =

expresas a las probabilidades de las intersecciones en función de las probabilidades condicionales y de las probabilidades de los sucesos condicionantes, y queda:

= p(C|V)*p(V) + p(C|R)*p(R) + p(C|A)*p(A) = 

reemplazas valores, y queda:

= (2/3)*(1/3) + 1*(1/3) + (1/2)*(1/3) =

= 2/9 + 1/3 + 1/6 =

= 13/18.

Luego, plantea:

p(R|C) = 

aplicas la definición de probabilidad condicional, y queda:

= p(R∩C)/p(C) =

expresas al numerador como producto entre la probabilidad condicional y la probabilidad del suceso condicionante "se eligió la moneda de la caja roja", y queda:

= p(C|R)*p(R)/p(C) =

reemplazas valores, y queda:

= 1*(1/3)/(13/18) =

= (1/3)/(13/18) =

= 6/13.

Espero haberte ayudado.

Vamos con una precisión:

El dominio de la función es: D = ]-2,-1] u ]2,+∞[.

Espero haberte ayudado.

Gracias, Silvio.

Observa que la tercera ecuación corresponde al plano OXY.

Observa que la primera ecuación corresponde a un cilindro parabólico paralelo al eje OZ, y observa que contiene a dicho eje, y que su intersección con el plano OXY (z = 0) es una parábola con vértice en el origen de coordenadas, que tiene al semieje OY positivo como parte significativa de su eje de simetría.

Observa que la segunda ecuación corresponde a un plano paralelo al eje OX, y una de sus ecuaciones explícitas es: z = 3 - (3/2)y, y observa que no contiene a dicho eje, y que su intersección con el plano OXY (z = 0) es una recta paralela al eje OX cuya ecuación es y = 2.

Luego, puedes hacer un gráfico (puedes apelar a algún programa informático para ello), y tienes:

que la "base" (R) del sólido es una porción de plano OXY limitada por la parábola y la recta que hemos descrito y cuyos vértices son los puntos (-1,2,0) y (1,2,0), y que su "techo" es una porción del plano cuya ecuación explícita hemos indicado, por lo que puedes plantear las inecuaciones dobles:

0 ≤ z ≤  3 - (3/2)y,

2x² ≤ y  ≤ 2,

-1 ≤ x  ≤ 1.

Observa que el sólido no tiene centro de simetría, por lo que no es conveniente plantear un cambio a coordenadas esféricas y observa que tampoco tiene eje de simetría, por lo que tampoco es conveniente planear un cambio a coordenadas cilíndricas.

Luego, puedes plantear para el volumen (observa que indicamos con corchetes que debes evaluar con Regla de Barrow):

V = 

= ∫∫∫_B 1*dz*dy*dx = ∫∫_R [ z ]*dy*dx = 

= ∫∫_R ( 3 - (3/2)y )*dy*dx = = _-1∫¹ [ 3y - (3/4)y² ]*dx =

= _-1∫¹ ( (6 - 3) - (6x² - 3x⁴) )*dx = _-1∫¹ ( 2 - 6x² + 3x⁴ )*dx = _-1∫¹ [ 2x - 2x³ + (3/5)x⁵ ]*dx = 

= (2 - 2 + 3/5) - (-2 +2 - 3/5) = 6/5.

Espero haberte ayudado.

Me ayudo bastente!!

Muy claro para explicar detalladamente, se agradece !!!

Muchas Gracias !!! 

Está bien el enunciado?? Estoy intentando calcularlo y no me sale...

Gabriel:  1^infinito es una indeterminación.

Pero si sustituyes te sale 1^-∞ por lo que saldría el exponente negativo... Acaso 1^∞=1^-∞ ???