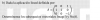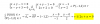-
Antonius Benedictus
el 12/4/18Sonia Ramis García
el 12/4/18Rasyer
el 12/4/18R² ----> R³ quiere decir que la aplicación lineal transforma un vector de R² a uno de R³. Por lo tanto el vector pasa de tener 2 coordenadas a tener 3.
Cuando dice caracterícense yo creo que se refiere a lo que ha escrito Antonio:
la imagen de f es el subespacio generado por los vectores (1, -1, 1) y (2, 0, 1)
el subespaacio Null es la solución trivial: el vector (0,0,0).
-
Antonius Benedictus
el 12/4/18¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
Antonio Silvio Palmitano
el 12/4/18Comienza por plantear la ecuación general de las curvas de nivel de la función:
F(x,y) = k, con k ∈ R;
luego, sustituyes la expresión de la función en el primer miembro, y queda:
3x2 - y2x - xy3 = k;
luego, evalúas para el punto en estudio: A(2,0), y queda: 12 = k;
luego, tienes una ecuación implícita de la curva de nivel de la función, con el punto en estudio perteneciente a ella:
3x2 - y2x - xy3 = 12;
y recuerda (revisa tus apuntes de clase), que el gradiente de la función evaluado en el punto en estudio es un vector normal para esta superficie, a la cuál dicho punto pertenece, y para calcularlo, comienza por plantear la expresión general del vector gradiente de la función:
∇F(x,y) = < Fx , Fy > = < 6x+y2-y3 , 2yx-3xy2 >,
luego evalúas para el punto en estudio y queda:
∇F(2,0) = < 12 , 0 >,
que es un vector normal a la curva de nivel que pasa por el punto A(2,0).
Espero haberte ayudado.
-
Antonius Benedictus
el 12/4/18¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).