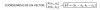Estudio completo de una funcion logaritmica

Si tienes la ecuación:

(6x² - 12)/(3x-4) =2x, multiplicas en ambos miembros por (3x-4), simplificas en el primer miembro, y queda:

6x² - 12 = 2x*(3x-4), distribuyes en el segundo miembro, y queda:

6x² - 12 = 6x² - 8x, haces pasajes de términos, reduces términos semejantes (observa que tienes cancelaciones), y queda:

8x = 12, divides por 8 en ambos miembros, simplificas, y queda:

x = 3/2, y puedes verificar que la solución remarcada es válida.

Espero haberte ayudado.

Vamos con una orientación.

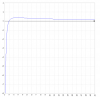
Plantea la expresión de la función continua y derivable con dominio en el conjunto de los números reales:

f(x) = x¹⁸ - 5x + 3 (*).

Luego, plantea la expresión de su función derivada primera:

f ' (x) = 18x¹⁷ - 5 (1).

Luego, plantea la expresión de su función derivada segunda:

f ' ' (x) = 306*x¹⁶ (2).

Luego, plantea la condición de punto crítico (posible máximo o posible mínimo de la función):

f ' (x) = 0, sustituyes la expresión señalada (1), y queda:

18x¹⁷ - 5 = 0, sumas 5 en ambos miembros, y queda:

18x¹⁷ = 5, divides por 18 en ambos miembros, y queda:

x¹⁷ = 5/18, extraes raíz de índice 17 en ambos miembros, y queda:

x = ¹⁷√(5/18) ≅ 0,9274.

Luego, evalúas el valor crítico remarcado en la expresión de la función derivada segunda señalada (2), y queda:

f ' ' ( ¹⁷√(5/18) ) = 306*( ¹⁷√(5/18) )¹⁶ = 306*(5/18)^16/17≅ 91,6521 > 0,

por lo que tienes que el valor remarcado corresponde a un mínimo en la gráfica de la función,

y, además, observa que la expresión de la función derivada segunda toma valores positivos para todo valor real distinto del valor crítico remarcado, por lo que tienes que la gráfica es cóncava para arriba en todo el dominio de la función, y como no presenta otros valores críticos, tienes que la función es decreciente para valores menores al valor crítico remarcado, y que es crecientes para valores mayores; y, observa el valor que toma la función para el valor crítico:

f( ¹⁷√(5/18) ) = ( ¹⁷√(5/18) )¹⁸ - 5( ¹⁷√(5/18) ) + 3 ≅ -1,3795 < 0;

luego, observa que para dos valores, uno menor y otro mayor que el valor crítico remarcado:

f(-2) = (-2)¹⁸ - 5(-2) + 3 > 0,

f(2) =  2¹⁸ - 5(2) + 3 = 2¹⁸ - 10 + 3 = 2¹⁸ - 7 > 0,

y observa que para ambos valores la función toma valores∞ positivos, por lo que tienes:

que existe un valor c₁ perteneciente al intervalo: ( -∞ , ¹⁷√(5/18) ), para el cuál la función toma el valor cero;

y que existe un valor c₂ perteneciente al intervalo: ( ¹⁷√(5/18) ,  +∞  ), para el cuál la función toma el valor cero.

Espero haberte ayudado.

Hola, esto tiene un error porque se solucionaría con el tema de Bolzano y el de Rolle pero no sé cómo

Muchas gracias

Vamos con el Teorema de Bolzano:

inspeccionas algunos valores que toma la función (observa que es continua en R), y tienes:

f(0) = 3 > 0,

f(1) = -1 < 0,

f(2) = 2¹⁸ - 7 > 0;

luego, tienes que la función toma valores con signos opuestos en el intervalo [0,1], por lo que tienes que existe un valor c₁ perteneciente a este intervalo para el cuál la función toma el valor cero;

luego, tienes que la función toma valores con signos opuestos en el intervalo [1,2], por lo que tienes que existe un valor c₂ perteneciente a este intervalo para el cuál la función toma el valor cero.

Luego, puedes inferir que el primer término de la expresión de la función toma valores positivos enormes comparados con los valores que toman los otros dos términos, por lo que es esperable que la función tome valores positivos para valores de la variable independiente mayores que 2, y observa que para valores de la variable independiente menores que cero tienes que la función toma valores positivos.

Observa que hasta aquí hemos demostrado que existen dos raíces, pero no hemos asegurado que son las únicas.

Espero haberte ayudado.

Discutir un sistema - Método de Gauss

Tienes que aclarar qué método os han explicado.

Yo lo he intentado resolver por Gauss, pero quieren que lo hagamos por Rouché y resolver por Cramer

Muchas gracias Antonio de verdad. No me había dado cuenta que me habías respondido. Me ha ayudado bastante y estoy muy agradecido de verdad. Mañana me gustaría colgar aquí el resto de ejercicios resueltos por mi para ver si están correctos. Necesito presentarlos bien y esto me ha ayudado un montón.

Mil gracias de verdad Antonio, no sabes cuanto me has ayudado.

Un saludo

Hola. Dos magnitudes son directamente proporcionales si cuando una aumenta, la otra tb, si una disminuye, la otra tb, y lo hacen proporcionalmente. Si divides los dólares entre las pulgadas de cada pizza y te da el mismo precio por pulgada en todas, las pulgadas y los dólares son directamente proporcionales. Si no lo son, verás ensegida cual conviene comprar, la que cueste menos por pulgada.

1/5

Está bien.

Por que piensas que hay fallo? No lo hay.

Gracias, Relío.