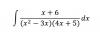-
lbp_14
el 2/4/18Hola Unicoos
He planteado la relacion de proporcionalidad entre sus componentes porque los vectores AB Y AC tienen que ser paralelos, pero no me sale porque me quedan dos incógnitas. Me podrían ayudar?
Averigua los valores de p y q para que los puntos A(4,-2,1) B(1,0,9) y C(0,p,q) estén alineados.
Muchas gracias
-
Enrique Vazquez
el 2/4/18¡Hola buenas! no paro de comerme el coco con el ejercicio que dice así:
Comprueba si los números 2,0 y 1 pertenecen al dominio de la función f(x) = √1/1-x y escribe 3 que no pertenezcan. En teoría el 1 no lo sería porque el dominio es todos los reales menos el 0, no?
Rasyer
el 2/4/18El dominio de tu función √(1/1-x ) es todos los reales des de menos infinito hasta 1 no incluído. -∞ < x < 1.
Esto se debe a dos motivos: Las raíces cuadradas tan solo aceptan valores positivos (y el zero); y en una fracción el denominador no puede ser 0.
Por lo tanto ni el número 2 ni el 1 pertenecen al dominio de la función, porque el 2 hace el interior de la raíz negativo y el 1 provoca una indeterminación en la fracción.
Otros 3 números que no pertenecen al dominio serían 10 1.0000001 y 5. En definitiva, cualquier número igual o mayor que 1.
-
Yessica Montero
el 2/4/18 -
Yessica Montero
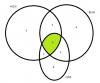
el 2/4/18Hola Profesor David. Dejo aquí mi Pregunta. En una clase de 30 estudiante. 15 obtuvieron 100 ptos en el examen de lógica 14 obtuvieron 100 ptos en el examen de conjunto 20 obtuvieron 100 ptos en el examen de desiguadades 5 obtuvieron 100 en el examen de log y conjunto 9 obtuvieron 100 ptos en el examen de log y desiguadades 7 obtuvieron 100 ptos en el examen de conjunto y desigualdad. Ni hubo ninguno sin un 100. Cuantos de ellos sacaron 100 en los tres?
LLame A{Examen de lógica}
B{Examen de conjunto}
C{Examen de desigualdad}
Hice mi diagrama de Venn, ubique las cantidades en las intersecciones. A(Inter)B=5, A(inter)C=9, B(inter)C=7. Pero como no supe hallar la cantidad en la inter ABC, no logre hallar el valor A, B, C total.
Antonio Silvio Palmitano
el 2/4/18Tienes los datos:
|A∪B∪C| = 30,
|A| = 15,
|B| = 14,
|C| = 20;
|A∩B| = 5,
|A∩C| = 9,
|B∩C| = 7,
|A∩B∩C| = x (a determinar).
Luego, recuerda la relación entre los cardinales para la unión de tres conjuntos:
|A∪B∪C| = (|A| + |B| + |C|) - (|A∩B| + |A∩C| + |B∩C|) + |A∩B∩C|.
Luego, sustituyes las expresiones de los cardinales, y queda:
30 = (15 + 14 + 20) - (5 + 9 + 7) - x,
resuelves términos en el segundo miembro, y queda:
30 = 49 - 21 + x,
restas 49 y sumas 21 en ambos miembros, y queda:
2 = x.
Espero haberte ayudado.
-
Carlos
el 2/4/18Hola buenas tardes. ¿Alguien me puede ayudar con esta integral racional? Muchas gracias
Antonio Silvio Palmitano
el 2/4/18Debes aplicar el Método de las Fracciones Simples:
(x+6) / (x2-3x)*(4x+5) = (x+6) / x*(x-3)*(4x+5) = a/x + b/(x-3) + c/(4x+5) = ( a*(x-3)*(4x+5) + b*x*(4x+5) + c*x*(x-3) ) / x*(x-3)*(4x+5).
Luego, por igualdad entre expresiones algebraicas fraccionarias, puedes plantear que los numeradores son iguales, y queda la igualdad entre polinomios:
a*(x-3)*(4x+5) + b*x*(4x+5) + c*x*(x-3) = x+6,
luego, evalúas para tres valores distintos (observa que los más convenientes son x = 3, x = 0 y x = -5/4), y queda:
51*b = 9, aquí divides por 51 en ambos miembros, simplificas, y queda: b = 3/17,
-15*a = 6, aquí divides por -15 en ambos miembros, simplificas, y queda: a = -2/5,
85/16*c = 19/4, aquí multiplicas en ambos miembros por 16/85, y queda: c = 76/85.
Luego, con el primer miembro y el tercer miembro de la cadena de igualdades entre expresiones algebraicas fraccionarias, tienes que la expresión del argumento de la integral queda:
(x+6) / (x2-3x)*(4x+5) = -(2/5)*(1/x) + (3/17)*( 1/(x-3) ) + (76/85)*( 1/(5x+4) ).
Luego, integras término a término, y la integral de tu enunciado queda:
I = -(2/5)*ln|x| + (3/17)*ln|x-3| + (76/425)*ln|5x+4| + C.
Espero haberte ayudado.
-
Roy
el 2/4/18en el ejercicio 2 he hallado a pe
ro nose puede hallar la derivabilidad así, que hice mal?
Antonio Silvio Palmitano
el 2/4/18Puedes plantear la expresión de la función derivada (recuerda que ya tienes el valor: a = 1, para el cuál la función es continua en x = 0), y observa que tienes una epresión a trozos:
f ' (x) =
ex si x < 0
a determinar si x = 0
e-x^2 - 2*x2*e-x^2 si x > 0
Luego, puedes tomar los límites laterales para x tendiendo a cero:
Lím(x→0-) f ' (x) = Lím(x→0-) ex = 1,
Lím(x→0+) f ' (x) = Lím(x→0+) (e-x^2 - 2*x2*e-x^2) = 1;
por lo que puedes inferir que la función derivada es continua para el valor en estudio (x = 0) y que para él toma el valor 1;
luego completas la expresión de la función derivada, y queda:
f ' (x) =
ex si x < 0
1 si x = 0
e-x^2 - 2*x2*e-x^2 si x > 0.
Espero haberte ayudado.
-
Roy
el 2/4/18No se como resolver
este ejercicio, me ayudan?
Antonio Silvio Palmitano
el 2/4/18Tienes la expresión de la función:
f(x) = a*x3 + b*x2 + c*x + d (*);
luego, planteas las expresiones de las funciones derivadas primera y segunda, y queda:
f ' (x) = 3*a*x2 + 2*b*x + c (1),
f ' ' (x) = 6*a*x + 2*b (2).
Luego, vamos con cada dato del enunciado por separado.
1)
La gráfica presenta un máximo en x = -1:
f ' (-1) = 0,
f ' ' (-1) < 0;
sustituyes las expresiones señaladas (1) (2) evaluadas en los primeros miembros, y queda:
3*a - 2*b + c = 0 (3),
-6*a + 2*b < 0 (4).
2)
La gráfica corta al eje OX en x = -2:
f(-2) = 0;
sustituyes la expresión señalada (*) evaluada en el primer miembro, y queda:
-8*a + 4*b - 2*c + d = 0 (5).
3)
La gráfica presenta una inflexión en x = 0:
f ' ' (x) = 0;
sustituyes la expresión señalada (2) evaluada en el primer miembro, y queda:
2*b = 0, aquí divides por 2 en ambos miembros, y queda: b = 0.
4)
La gráfica presenta recta tangente cuya pendiente es 9 en x = 2:
f ' (2) = 9;
sustituyes la expresión señalada (1) evaluada en el primer miembro, y queda:
12*a + 4*b + c = 9 (6).
Luego, reemplazas el valor remarcado en las ecuaciones señaladas (3) (5) (6), cancelas términos nulos, y queda el sistema:
3*a + c = 0, aquí restas 3*a en ambos miembros, y queda: c = -3*a (7),
-8*a - 2*c + d = 0,
12*a + c = 9.
Luego, sustituyes la expresión señalada (7) en las dos últimas ecuaciones, reduces términos semejantes, y queda:
-2*a + d = 0, aquí sumas 2*a en ambos miembros, y queda: d = 2*a (8),
9*a = 9, aquí divides por 9 en ambos miembros, y queda: a = 1;
luego, reemplazas este valor remarcado en las ecuaciones señaladas (8) (7), resuelves, y queda: d = 2 y c = -3.
Luego, observa que se verifica la inecuación señalada (4);
luego, reemplazas los valores remarcados en la expresión de la función señalada (*), cancelas el término nulo, y queda:
f(x) = x3 - 3*x + 2.
Espero haberte ayudado.
-
Sara Bach Fou
el 2/4/18Muchas gracias, Benito!
Pero sigo teniendo dudas con el tema de los intervalos, en un límite, por ejemplo este otro ejercicio:
¿ Cómo se solucionaría?¿ Tendría que calcular cuándo es continua la función, y en las discontinuidades que se den sería que la función se anula?
Gracias de antemano de nuevo!
-
Sara Bach Fou
el 2/4/18
Buenos días! Tengo que resolver esta pregunta y no encuentro cómo hacerlo en los vídeos de límites de David. ¿ Tendría que hallar el límite de esta función para X mayor que 0 y menor que dos? ¿cómo sabría cuales son los máximos y los mínimos sin dibujar el resto de la función?
¿Me podríais explicar cómo se resuelve? Mil gracias de antemano!!
-
Richie
el 2/4/18
