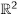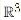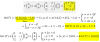-
Suponga A pertenece M3x2 y b pertenece M3x2 (R) donde, b=/=0, si W es un conjunto de soluciones del sistema Ax=b. Demuestre que W no es subespacio.
No se como plantearlo pues no tengo idea que significa Ax en la matriz.
Antonius Benedictus
el 31/3/18Angel Garcia Curela
el 31/3/18Angel Garcia Curela
el 31/3/18Antonius Benedictus
el 31/3/18Bueno, vamos aclarando cosas,
Si b es una matriz 3x1 (o sea un vector de IR^3) no nula, entonces el vector x=(0,0,0) (en columna) no es solución del sistema (pues éste no es homogéneo). Por tanto W (subespacio de soluciones) no posee el vector nulo. Entonces W no puede ser subespacio vectorial.
-
¿Qué significa L( ) en estos limites? Nunca había visto dicha nomenclatura y realizando búsquedas en internet no me arroja ningún resultado
Antonius Benedictus
el 31/3/18Juan Lorenzo
el 31/3/18Antonius Benedictus
el 31/3/18 -
por favor podrian ayudarme como solucionar los ejercicios (3, 8 y 10), los demas ejercicios ya hice solo me faltan eses 3 ejercicios. muchas gracias..

Antonius Benedictus
el 31/3/18¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
Alejandro Legaspe
el 1/4/18Para el 8 hay que usar la defincion de las coordenas del centroide,digamos que son (a,b), vienen dados por
a=∫∫xds/∫∫ds, donde S es la superficie donde vamos a integrar, ve que y2 =x+9 la podemos ver como funcion de x, asi y=√x+9, por otro lado el segundo cuadradante, x<0,y>0, por lo que nuestra superficie S es esa porcion de la grafica delimitada por los ejes,nota que,en esta superficie, 0<y<√x+9 y -9<x<0, asi, ya solo hay que evaluar las integrales para hallar el centroide
∫∫xds=∫∫xdydx (la primer integral de izquierda a derecha va de x=-9 a x=0 y la segunda va de y=0 a y=√x+9
∫∫ds=∫∫dydx ((la primer integral de izquierda a derecha va de x=-9 a x=0 y la segunda va de y=0 a y=√x+9 )
Asi,a ya estaria determinado,solo "quedaria" hacer el calculo de esas integrales
Para b lo definen como b=∫∫yds/∫∫ds,analogamente,se tiene que
∫∫yds=∫∫ydydx (la primer integral de izquierda a derecha va de x=-9 a x=0 y la segunda va de y=0 a y=√x+9
∫∫ds=∫∫dydx ((la primer integral de izquierda a derecha va de x=-9 a x=0 y la segunda va de y=0 a y=√x+9 )
Para el 10 es bastante similar, nota si 0<x<π/3, y que para estas x, 0<y<2sen(3x) es la superficie donde vamos a integrar, asi
a= ∫∫xds/∫∫ds
∫∫xds=∫∫xdydx (la primer integral de izquierda a derecha va de x=0 a x=π/3 y la segunda va de y=0 a y=2sen3x
∫∫ds=∫∫dydx ((la primer integral de izquierda a derecha va de x=0 a x=π/3 y la segunda va de y=0 a y=2sen3x
Asi a ya queda determinado con hacer el calculo de estas integrales, y para b se tiene que
∫∫yds=∫∫ydydx (la primer integral de izquierda a derecha va de x=0 a x=π/3 y la segunda va de y=0 a y=2sen3x
∫∫ds=∫∫dydx ((la primer integral de izquierda a derecha va de x=0 a x=π/3 y la segunda va de y=0 a y=2sen3x
por lo que el centroide es (a,b)
-
Que resultado da esto:
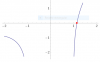
-Calcula el área encerrada por y = x3–x2– 9x y el eje OX
Antonio Silvio Palmitano
el 31/3/18Observa que tienes la ecuación de la gráfica de una función continua en R, y del eje OX, que es: y = 0.
Luego, igualas expresiones, y queda la ecuación:
x3 - x2 - 9x = 0, extraes factor común, y queda:
x*(x2 - x - 9) = 0;
luego, por anulación de un producto, tienes dos opciones:
x = 0,
y también:
x2 - x - 9 = 0, que es una ecuación polinómica cuadrática, cuyas soluciones son:
x = ( 1 - √(37) )/2 ≅ -2,541,
x = ( 1 + √(37) )/2 ≅ 3,541.
Luego, evalúa la expresión de la función para valores intermedios (por ejemplo: x1 = -1 y x2 = 1, y tienes:
y1 = -1 - 1 + 9 = 7 > 0,
y2 = 1 - 1 - 9 = - 9 < 0;
y puedes visualizar que tienes dos regiones:
R1: región "por encima" del eje OX, comprendida entre xa = ( 1 - √(37) )/2 y xb = 0,
R2: región "por debajo" del eje OX, comprendida entre xb = 0 y xc = ( 1 + √(37) )/2.
Luego, puedes plantear la expresión del área requerida en tu enunciado:
A = A1 + A2 = (1-√(37))/2∫0 ( (x3 - x2 - 9x) - (0) )*dx + 0∫(1+√(37))/2 ( (0) - (x3 - x2 - 9x) )*dx =
reduces las expresiones de los argumentos de las integrales, y queda.
= (1-√(37))/2∫0 (x3 - x2 - 9x)*dx + 0∫(1+√(37))/2 (-x3 + x2 + 9x) )*dx = y puedes continuar la tarea.
Espero haberte ayudado.