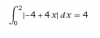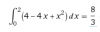Vamos con una orientación.

Plantea las expresiones de los vectores: 

A = <p,q,r> y B = <x,y,z>.

Luego, plantea la expresión del producto vectorial entre ellos:

AxB = <qz-ry,rx-pz,py-qx>,

y luego plantea la expresión del cuadrado del módulo del producto vectorial:

|AxB|² = (qz-ry)² + (rx-pz)² + (py-qx)² (1).

Luego, plantea la expresión del cuadrado del módulo del producto vectorial en función del ángulo determinado por los vectores:

|AxB|² = |A|²*|B|²*sen²θ =

aplicas la identidad trigonométrica del cuadrado del seno en función del cuadrado del coseno, y queda:

= |A|²*|B|²*(1 - cos²θ) =

distribuyes, y queda:

= |A|²*|B|² - |A|²*|B|²*cos²θ =

asocias potencias en el segundo término, y queda:

= |A|²*|B|² - (|A|*|B|*cosθ)² =

sustituyes la expresión del producto escalar entre los vectores en el argumento de la potencia en el segundo término, y queda:

= |A|²*|B|² - (A•B)² =

expresas los módulos de los vectores y el producto escalar en función de las componentes de los vectores, y queda:

= (p² + q² + r²)*(x² + y² + z²) - (px + qy + rz)² (2).

Luego, queda la tarea de desarrollar las expresiones señaladas (1) (2), para hacer evidente que conducen a una misma expresión.

Espero haberte ayudado.

Si no pones el enunciado original (con los datos de los vectores) va a resultar difícil ayudarte.

Ay! Lo siento! Te los digo ahora:

muchas gracias Antonio

¡Correcto!

Tienes la expresión de la función:

p(x) = a*x³ + b*x² + c*x + d (*).

Luego, plantea la expresión de la función derivada primera:

p ' (x) = 3*a*x² + 2*b*x + c (1).

Luego, plantea la expresión de la función derivada segunda:

p '' (x) = 6*a*x + 2*b (2).

Luego, vamos con cada dato por separado:

a)

Plantea la condición de punto crítico (posible máximo o posible mínimo de la función), para x = 1:

p ' (1) = 0, sustituyes la expresión señalada (1) evaluada en el primer miembro, y queda:

3*a + 2*b + c = 0 (3).

b)

Plantea la condición de pertenencia a la gráfica para el punto en estudio A(0,1):

p(0) = 1, sustituyes la expresión señalada (*) evaluada en el primer miembro, y queda:

d = 1.

Plantea la condición de posible punto de inflexión, para x = 0:

p '' (0) = 0, sustituyes la expresión señalada (2) evaluada en el primer miembro, y queda:

2*b = 0, divides por 2 en ambos miembros, y queda:

b = 0.

c)

Tienes la integral definida:

₀∫¹ p(x)*dx = 5/4, sustituyes la expresión señalada (*) en el argumento de la integral, y queda:

₀∫¹ ( a*x³ + b*x² + c*x + d )*dx = 5/4, integras (observa que indicamos con corchetes que debes evaluar con Regla de Barrow), y queda:

[ (a/4)*x⁴ + (b/3)*x³ + (c/2)*x² + d*x ] = 5/4, evalúas (observa que cancelamos los términos nulos), y queda:

a/4 + b/3 + c/2 + d = 5/4, multiplicas por 12 en todos los términos de la ecuación, y queda:

3*a + 4*b + 6*c + 12*d = 15 (4).

Luego, reemplazas los valores remarcados en las ecuaciones señaladas (3) (4), cancelas los términos nulos, y queda el sistema de ecuaciones:

3*a + c = 0, aquí restas 3*a en ambos miembros, y queda: c = -3*a (5),

3*a + 6*c + 12 = 15;

luego, sustituyes la expresión señalada (5) en la última ecuación, y queda:

3*a - 18*a + 12 = 15, restas 12 en ambos miembros, reduces términos semejantes, y queda:

-15*a = 3, divides por -15 en ambos miembros, y queda:

a = -1/5;

luego, reemplazas el último valor remarcado en la ecuación señalada (5), y queda:

c = 3/5.

Luego, reemplazas los valores remarcados en la ecuación señalada (*), cancelas el término nulo, y la expresión de la función queda:

p(x) = -(1/5)*x³ + (3/5)*x + 1;

y la expresión de la función derivada primera queda:

p ' (x) = -(3/5)*x² + 3/5;

y la expresión de la función derivada segunda queda:

p '' (x) = -(6/5)*x;

y luego puedes verificar:

que la función derivada primera toma el valor cero para x = 1, que corresponde a un punto crítico;

que la función derivada segunda toma un valor negativo para x = 1, por lo que tienes un máximo relativo;

que la función derivada segunda toma el valor cero para x = 0, que corresponde a un punto de inflexión, ya que la función derivada primera toma un valor positivo.

Espero haberte ayudado.

¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que  lo entiendas.

Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).

Hola,  estuve buscando por si había algún vídeo y como lo encontré entonces escribe por si se me paso el vídeo o algo, pero ya veo que no, de igual manera lo entiendo y gracias.