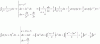-
¿Cual es la definición recursiva de esta sucesión?
0, 1, 1/2, 5/6, 7/12, ....
Ángel
el 30/3/18Suponemos que los primeros términos tienen un valor fijo (como por ejemplo la sucesión de Fibonacci: a1=1, a2=1, an=an-1+an-2 )
En tu sucesión en particular:
a1=0/1 = N1/D1
a2= 1/1 = N2/D2
a3= 1/2 = N3/D3
a4= 5/6 = N4/D4
Suponemos que, a partir de aquí, los números sucesivos estarán relacionados como lo está el quinto término con los demás términos. Observa que el numerador del quinto término es la suma de los numeradores anteriores, igual con el producto de los denominadores anteriores:
a5= (5+1+1+0)/(6*2*1*1) = 7/12
a6= (7+5+1+1+0)/(12*6*2*1*1) = 14/144
.
.
an= (N1+N2+N3+...+Nn-1)/(D1*D2*D3*...*Dn-1) = (n-1∑n=1 Nn )/(n-1∏n=1 Dn )
Antonio Silvio Palmitano
el 30/3/18Comienza por expresar en forma explícita al primer elemento de la sucesión:
a0 = 0,
Luego, planteas las restas de cada elemento con su elemento precedente, y tienes:
a1 - a0 = 1 - 0 = 1 = (-1)2/1,
a2 - a1 = 1/2 - 1 = -1/2 = (-1)3/2,
a3 - a2 = 5/6 - 1/2 = 1/3 = (-1)4/3,
a4 - a3 = 7/12 - 5/6 = -1/4 = (-1)5/4,
y observa que puedes inferir una expresión recursiva para las diferencias:
an - an-1 = (-1)n+1/n, aquí sumas an-1 en ambos miembros, y queda: an = an-1 + (-1)n+1/n,
con n ∈ N, n ≥ 1.
Luego, con las ecuaciones remarcadas, puedes inferir una definición de la sucesión en forma recursiva:
a0 = 0,
an = an-1 + (-1)n+1/n,
con n ∈ N,
n ≥ 1.
Espero haberte ayudado.
-
Hola, necesito ayuda con una integral, se que no tiene solución por que lo ingrese en diferentes programas y lo intente hacer de muchas maneras, Se me pide que realice la integral utilizando método de sustitución. Lo que necesito es saber por que esta integral no tiene solución.

Antonius Benedictus
el 29/3/18Rodrigo Perez
el 29/3/18 -
Me ayudarían con este problema (no sé ni cómo empezarlo):
P es un punto en el primer cuadrante sobre la curva y = 7 − x^2. Por P se traza la tangente a la curva y sean A y B los puntos en que corta a los ejes coordenados. Hallar la ordenada de P para que AB sea mínimo.
Antonio Silvio Palmitano
el 30/3/18Si la pregunta de tu enunciado hace referencia a que la multiplicación M = A*B debe ser mínima:
tienes en el desarrollo del colega Antonio las expresiones correspondientes: A = (x02+7)/(2x0), B = x02+7,
y la multiplicación queda expresada:
M = (x02+7)2/(2x0), desarrollas el numerador, distribuyes el denominador, simplificas (te dejo la tarea), y queda:
M = (1/2)x03 + 7x0 + (49/2)x0-1 (*),
cuya función derivada primera tiene la expresión:
M ' = (3/2)x02 + 7 - (49/2)x0-2 (1),
y cuya función derivada segunda tiene la expresión:
M ' ' = 3x0 + 49x0-3. y observa que esta expresión toma valores positivos para puntos pertenecientes al primer cuadrante.
Luego, planteas la condición de valor crítico (posible máximo o posible mínimo para la multiplicación), y queda:
M ' = 0, sustituyes la expresión señalada (1), y queda:
(3/2)x02 + 7 - (49/2)x0-2 = 0, multiplicas en todos los términos de la ecuación por 2x02, y queda:
3x04 + 14x02 - 49 = 0,
que es una ecuación polinómica "bicuadrática", por lo que aplicas la sustitución (cambio de incógnita): x02 = w (3), observa que w toma valores positivos, y queda:
3w2 + 14w - 49 = 0,
que es una ecuación polinómica cuadrática, cuyas soluciones son:
w = -,7, que no tienes sentido para este problema (recuerda que w toma valores positivos),
w =7/3, sustituyes la expresión señalada (1), y queda:
x02 = 7/3,
compones en ambos miembros con la función raíz cuadrada (observa que elegimos la solución positiva, porque el punto P pertenece al primer cuadrante), y queda:
x0 = √(7/3),
que es el valor de la abscisa del punto de tangencia, y observa que para él la derivada segunda de la función Multiplicación toma un valor positivo, por lo que tienes que el valor remarcado corresponde a un mínimo;
luego, evalúas la expresión de la función para el valor remarcado, y queda:
y = -( √(7/3) )2 + 7, resuelves y queda:
y0 = 14/3,
que es el valor de la ordenada del punto de tangencia, que queda expresado:
P( √(7/3) , 14/3 ), que pertenece al primer cuadrante.
Espero haberte ayudado.
-
Hola buenos dias me podrian colaborar con varios ejercicios de moda, mediana, media y cuartiles de estadistica para practicar (con respuestas para comparar), muchas gracias.
-
Me podriais decir los resultados para poder comprobarlos?
Dados los puntos A(3, -2) y B(5, 4):
- Halla la ecuación general de la recta r que pasa por A y B
- Halla la mediatriz del segmento AB
- Halle el punto simétrico del punto B respecto del A
- Halla el valor de K para que los puntos A, B y P(3, K) estén alineados
Gracias de antemano
-
Me podrían ayudar con los siguientes ejercicios por favor?
A) En un grupo de 40 alumnos hay 27 aprobados. Si de eligen 6 alumnos al azar, ¿cuál es la probabilidad de que 4 de ellos hayan aprobado?
B) Determina la probabilidad de:
a) Obtener tres veces un 2 en cinco lanzamientos de un dado.
b) Obtener tres veces seguidas un 2 en cinco lanzamientos de un dado.
C) La urna A contiene 3 bolas negras y 5 blancas, y la urna B, 4 negras y 6 blancas. Se escoge una bola de la urna A y se introduce en
la urna B. A continuación, se extrae una bola de la urna B.
a) ¿Cuál es la probabilidad de que sea blanca?
b) Si la bola extraída ha sido blanca, ¿cuál es la probabilidad de que la bola extraída de la urna A fuese blanca?