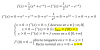-
Paula
el 1/4/18 -
Antonio Omg
el 1/4/18como puedo hacer q estas ecuaciones: AX^2 - 4X +1 = 0 -X^2 + AX - 4=0 tengan una solucion, dos doluciones , y ninguna solucion
gracias!
Alejandro Legaspe
el 1/4/18Siguiendo la idea,hay que analizar el discriminante (-4)²-4A(1)=16-4A
La ecuacion tendra una solucion si 16-4A=0, entonces A=4
tendra dos soluciones si 16-4A>0, Entonces A<4
Y no tendra soluciones en los reales si 16-4A<0 entonces 4<A
El otro es similar,si tienes dudas nos cuentas
-
Maria Aguilar Guerrero
el 1/4/18 -
Pamela Zambrano
el 1/4/18
Antonio Silvio Palmitano
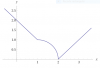
el 1/4/18
Divides la figura según su eje de simetría que pasa por el centro del círculo y, luego, observa el triángulo rectángulo sombreado en amarillo, y tienes:
senα = h/r = reemplazas valores = ( √(2)/2 ) / 1 = √(2)/2;
luego, compones con la función inversa del seno, y queda:
α = 45°;
luego, puedes plantear:
x/r = cosα, multiplicas en ambos miembros por r, y queda:
x = r*cosα = 1*√(2)/2 = √(2)/2 cm.
Luego, tienes para la longitud de la base menor del trapecio:
b = 2*x = 2*√(2)/2 = √(2) cm.
Espero haberte ayudado.
-
Sara Mrabet
el 1/4/18 -
GEMA ORTIZ DÍAZ
el 1/4/18Como se hace la derivada??
Alejandro Legaspe
el 1/4/18Derivada de una función 00 - Regla de la cadena
Habrá que derivarlo como una función elevado a un número,luego aplicar la regla de la cadena, entonces
f'(x)=2cos(3x2 -2x) d(cos(3x2 -2x))/dx=-2cos(3x2 -2x)sen(3x2 -2x) (6x-2)=-(6x-2)sen(6x2 -4x)
-
Bet
el 1/4/18
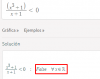
¿Cómo resuelvo esta inecuación?
Me pierdo bastante cuando queda como x2 -x+1<0 al despejar la suma de cubos con el de abajo
¿Como llego a que es Falsa usando la formula general y determinando soluciones?
Alejandro Legaspe
el 1/4/18La desigualdad se cumple en dos casos
1)(x3 +1)>0 y x+1<0
De x3 +1>0 se tiene que x3 >-1 es decir x>-1 y de x+1<0 se tiene que x<-1, es decir ninguna x cumple ambas condiciones
2) x3 +1)<0 y x+1>0
Análogamente, de x3 +1)<0 se llega a que x<-1 y de x+1>0, entonces x>-1, donde tampoco ninguna x cumple ésto, por lo que la desigualdad no tiene conjunto solución
-
Alejandro
el 1/4/18Buenas noches,
Calcula el área encerrada por y = x3–x2– 9x y el eje OX
Alejandro Legaspe
el 1/4/18Hay que encontrar los puntos de intersección de la funcion dada y y=0, es decir,
0=x3 -x2 -9x, que es x=0 y x2 -x-9=0, es decir x=(1±√37)/2, el area es la integral de y desde x=(1-√37)/2 hasta x=0 mas la integral (en valor absoluto) de y desde x=0 hasta x= (1+√37)/2
-
Joship
el 31/3/18
hi! Queria que me ayudaran a ver si estoy en el camino correcto para determinar el dominio (1 caso y 2 caso*), ahora nose como comprobar el recorrido. Se que lo de adentro tiene que ser positivo o cero pero nose... plis pido ayuda de ante mano, gracias -
Jesús B
el 31/3/18lim [(x^2+2) / 2-x^2] ^ 1 / x^2
x-->0
Espero puedan ayudarme. Gracias de antemano
Carlos Muñoz
el 1/4/18
Alejandro Legaspe
el 1/4/18En efecto es infinito, pero evaluando queda 1 al infinito,por lo que se puede usar la exponencial y su inversa, para usar propiedades del logaritmo,pues
(x2 +2)/(2-x2 )1/x2 =exp(ln((x2 +2)/(2-x2 )1/x2 )=exp(ln( (x2 +2)/(2-x2 ) )/x2 ) y hay que calcular el lim x-->0 de ln( (x2 +2)/(2-x2 ) )/ x2 , como es 0/0 se puede usar L'hopital, donde se
llega al lim x-->0 4(2x)(2-x2 )/(2-x2 ) 2 (x2 +2)(2x)=oo, así el límite es e^oo=oo
