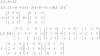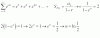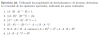-
me podéis decir como resolver este sistema por el método de sustitución
5x-2y=12
4x+3y=5
Zhang Vicente
el 16/3/18
En la primera ecuación, dejas x solo y queda x=(12+2y)/5. Después haces lo mismo en la segunda ecuación y da x=(5-3y)/4, pero puedes hacer lo mismo dejando solo las y también. Ahora, igualas las x de las dos ecuaciones que acabamos de sacar, (12+2y)/5=(5-3y)/4. Multiplicas por 20 ambos lados quedando 4(12+2y)=5(5-3y), despejas 48+8y=25-15y, -23y=23 y=1. Sustituyes y=1 en cualquiera de las dos ecuaciones del enunciado, 5x+2=12, x=2. Solución: x=1 y=2
Antonio Silvio Palmitano
el 16/3/18Vamos con una precisión.
Seguimos al colega Zhang hasta igualar las dos expresiones de la incógnita x como función de la incógnita y:
(12 + 2y)/5 = (5 - 3y)/4, multiplicas en ambos miembros por 20, simplificas, y queda:
4(12 + 2y) = 5(5 - 3y), distribuyes en ambos miembros, y queda:
48 + 8y = 25 - 15y, haces pasajes de términos, y queda:
8y + 15y = 25 - 48, reduces términos semejantes en ambos miembros, y queda:
23y = -23, divides por 23 en ambos miembros, y queda:
y = -1;
luego, tienes la primera expresión de la incógnita x como función de la incógnita y:
x = (12 + 2y)/5, reemplazas el valor remarcado, y queda:
x = ( 12 + 2(-1) )/5, resuelves el segundo término en el numerador, y queda:
x = (12 - 2)/5, resuelves el numerador, y queda:
x = 10/5, simplificas, y queda:
x = 2;
luego, tienes la segunda expresión de la incógnita x como función de la incógnita y:
x = (5 - 3y)/4, reemplazas el valor remarcado, y queda:
x = ( 5 - 3(-1) )/4, resuelves el segundo término en el numerador, y queda:
x = (5 + 3)/4, resuelves el numerador, y queda:
x = 8/4, simplificas, y queda:
x = 2;
por lo que tienes que se verifica que la solución del sistema de ecuaciones es: x = 2 e y = -1.
Espero haberte ayudado.
-
Hola, alguien podría decirme cómo se hace este ejercicio?
--> Dado el complejo 2_60º que es una solución de la raíz sexta de otro complejo, calcula el resto de soluciones?
Si es la raíz sexta haría 2_(60) / 2_(60+60)/ 2_(60+120) / 2_(60+180) etc ??
Gracias!
Antonio Silvio Palmitano
el 16/3/18Si. Es correcta tu respuesta.
w6 = (260°)6 = 266*60° = 64360° = 640° = 64 = z;
y las raíces sextas de z = 64 quedan expresadas: 6√(z) = 6√(640°) = 6√(64)(0°+k*360°)/6 = 2k*60°,
con k = 0, 1, 2, 3, 4, 5;
luego, reemplazas valores, y quedan: 260°, 2120°, 2180° = -2, 2240°, 2300° y 2360° = 20° = 2.
Espero haberte ayudado.
-
¡Hola Unicoos! ¿Podéis decirme como continúo con el ejercicio? La cuestión de Diagonalización no la tengo nada clara. Si continuáis el ejercicio, ya lo puedo tener como ejemplo para los demás.

Antonius Benedictus
el 16/3/18https://matrixcalc.org/es/#diagonalize%28%7B%7B3,1,0%7D,%7B0,3,0%7D,%7B1,0,1%7D%7D%29
Para a=1:
https://matrixcalc.org/es/#diagonalize%28%7B%7B1,1,0%7D,%7B0,3,0%7D,%7B1,0,1%7D%7D%29
-
Antonio Silvio Palmitano
el 16/3/18Vamos con los dos primeros.
1)
Tienes el determinante:
|A*(B*A)-1*B| = aplicas la propiedad del determinante de un producto de matrices:
= |A|*|(B*A)-1|*|B| = aplicas la propiedad del determinante de la matriz inversa:
= |A|*( 1/|A*B| )*|B| = aplicas la la propiedad del determinante de un producto de matrices:
= |A|*( 1/(|A|*|B| )*|B| = resuelves el producto entre fracciones:
= |A|*|B| / (|A|*|B| ) = simplificas:
= 1.
2)
Tienes el determinante:
|(A*B)t*(B-1)t| = aplicas la propiedad del determinante de un producto de matrices:
= |(A*B)t|*|(B-1)t| = aplicas la propiedad del determinante de la matriz traspuesta (|Xt| = |X|):
= |A*B|*|B-1| = aplicas la propiedad del determinante de la matriz inversa:
= |A*B|*( 1/|B| ) = aplicas la la propiedad del determinante de un producto de matrices:
=|A|*|B|*( 1/|B| ) = resuelves el producto entre fracciones:
= |A|*|B| / |B| = simplificas:
= |A|.
Espero haberte ayudado.
Antonio Silvio Palmitano
el 16/3/183)
Tienes el determinante:
|A-1*(B*A)t*B-1| = aplicas la propiedad del determinante de una multiplicación de matrices:
= |A-1|*|(B*A)t|*|B-1| = aplicas la propiedad del determinante de la matriz traspuesta:
= |A-1|*|B*A|*|B-1| = aplicas la propiedad del determinante de una multiplicación de matrices:
= |A-1|*|B|*|A|*|B-1| = aplicas la propiedad del determinante de la matriz inversa:
= ( 1/|A| )*|B|*|A|*( 1/|B| ) = resuelves el producto:
= |B|*|A| / (|A|*|B|) = simplificas:
= 1.
4)
Tienes la matriz
(B*At)-1*(B-1)-1*A = aplicas la propiedad de la matriz inversa de un producto de matrices:
= (At)-1*B-1(B-1)-1*A = aplicas la propiedad de la inversa de la matriz inversa:
= (At)-1*B-1B*A = aplicas la ley asociativa de la multiplicación de matrices:
= (At)-1*(B-1B)*A = aplicas la ley de existencia del inverso multiplicativo de la multiplicación de matrices:
= (At)-1*I*A = aplicas la ley asociativa de la multiplicación de matrices:
= (At)-1*(I*A) = aplicas la ley de existencia del elemento neutro de la multiplicación de matrices:
= (At)-1*A = aplicas la propiedad de la inversa de la matriz traspuesta:
= (A-1)t*A = aplicas la propiedad de la traspuesta de de la matriz traspuesta::
= (A-1)t*(At)t = aplicas la propiedad de la traspuesta de una multiplicación de matrices:
= (At*A-1)t.
5)
Tienes la matriz:
(A + B)2 = aplicas la definición de potencia de una matriz:
= (A + B)*(A + B) = aplicas la ley distributiva de la multiplicación de matrices con respecto a la suma:
= A*A + A*B + B*A + B*B = aplicas la hipótesis de tu enunciado (A*B = B*A):
= A*A + A*B + A*B + B*B = reduces términos semejantes:
= A*A + 2*A*B + B*B = aplicas la definición de potencia de una matriz:
= A2 + 2*A*B + B2.
6)
Tienes la matriz:
(A*B*A-1)2 = aplicas la definición de potencia de una matriz:
= (A*B*A-1)*(A*B*A-1) = aplicas la ley asociativa de la multiplicación de matrices:
= A*B*(A-1*A)*B*A-1 = aplicas la ley de existencia del elemento inverso de la multiplicación de matrices:
= A*B*I*B*A-1 = aplicas la ley asociativa de la multiplicación de matrices:
= A*B*(I*B)*A-1 = aplicas la ley de existencia del elemento neutro de la multiplicación de matrices:
= A*B*B*A-1 = aplicas la ley asociativa de la multiplicación de matrices:
= A*(B*B)*A-1 = aplicas la definición de potencia de una matriz:
= A*B2*A-1 ≠ B2;
porque la multiplicación de matrices no es conmutativa, y no puedes asociar los factores A y A-1.
Por lo tanto, tienes que las primeras cinco proposiciones son Verdaderas y la última es Falsa.
Espero haberte ayudado.