-
Antonio Silvio Palmitano
el 30/1/18Aplicas el Teorema Fundamental del Cálculo Integral, y la expresión de la función queda:
f(x) = arctan( 1/(x-a) ), cuyo dominio es: D = R - {a} = (-∞,a) u (a,+∞).
Luego, compones en ambos miembros con la función inversa del arco tangente, y queda:
tan( f(x) ) = 1/(x-a), expresas a la tangente en función de la cotangente, y queda:
1/cotg( f(x) ) = 1/(x-a), haces pasajes de divisores como factores, y queda:
x-a = cotg( f(x) ), compones en ambos miembros con la función inversa de la cotangente, y queda:
arccotg(x-a) = f(x);
por lo que tienes que una expresión equivalente de la función de tu enunciado es:
f(x) = arccotg(x-a), cuyo dominio es: D = R - {a} = (-∞,a) u (a,+∞).
1)
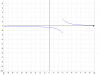
Asíntotas Horizontales:
Lím(x→-∞) f(x) = Lím(x→-∞) arccotg(x-a) = 0,
Lím(x→+∞) f(x) = Lím(x→+∞) arccotg(x-a) = 0,
por lo que tienes que la recta cuya ecuación es:
y = 0,
es asíntota horizontal de la gráfica de la función, por izquierda y por derecha.
2)
Asíntotas Verticales:
Lím(x→a-) f(x) = Lím(x→a-) arccotg(x-a) = -∞,
Lím(x→a+) f(x) = Lím(x→a+) arccotg(x-a) = +∞,
por lo que tienes que la recta cuya ecuación es:
x = a,
es asíntota vertical de la gráfica de la función, inferiro por izquierda y superior por derecha.
3)
Monotonía:
Planteas la expresión de la función derivada primera, y queda:
f ' (x) = -1/( 1+(x-a)2 ),
y observa que su denominador es estrictamente positivo y, como su numerador es igual a -1, tienes que la función derivada primera toma valores negativos, por lo que es decreciente en los dos subintervalos de su dominio.
4)
Curvatura:
Planteas la expresión de la función derivada segunda, y queda:
f ' ' (x) = 2*(x-a) / ( 1+(x-a)2 )2,
y observa que su denominador es estrictamente positivo, por lo que tienes dos opciones a partir del signo de la expresión que tienes en el numerador (observa que el numerador es distinto de cero en todo el dominio de la función):
4a)
2*(x-a) > 0, haces pasaje de factor como divisor, y luego haces pasaje de término, y queda: x > a,
por lo que tienes que la gráfica de la función es cóncava hacia arriba en el intervalo: (a,+∞);
4b)
2*(x-a) < 0, haces pasaje de factor como divisor, y luego haces pasaje de término, y queda: x < a,
por lo que tienes que la gráfica de la función es cóncava hacia arriba en el intervalo: (-∞,a),
Espero haberte ayudado.
-
Podríais explicarme el último paso de vuestra integral?. No entiendo pq se llega a x^4, quizás sea una propiedad de los números e?
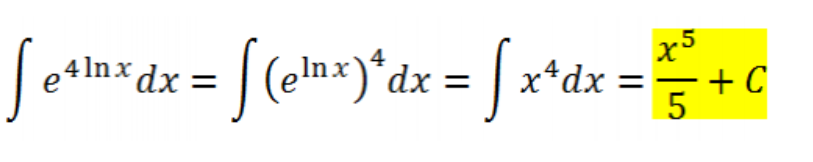
-
¿Cómo se podría resolver esto? Ya sé que si w∧v = 0 entonces w y v son ortogonales, por lo que supongo que el espacio será el de todos los vectores v tal que v sea ortogonal a w. No sé como seguir ni estoy muy seguro de lo que dije

-
Antonio Silvio Palmitano
el 30/1/18B)
Planteas la ecuación punto-pendiente de la recta r, y queda:
y - 3 = m*(x + 2) (1).
Planteas la condición de ordenada nula (y = 0), reemplazas en la ecuación de la recta s, cancelas el término nulo, y queda:
-2*x + (2*m - 4) = 0, haces pasaje de término, y queda:
-2*x = -(2*m - 4), multiplicas por -1 en ambos miembros, y queda:
2*x = 2*m - 4, divides por 2 en todos los términos de la ecuación, y queda:
x = m - 2, por lo que el punto de intersección de la recta s con el eje OX queda:
Q( (m - 2) , 0 ),
y la ecuación de la recta t, que es paralela al eje OY y pasa por el punto Q queda:
x = m - 2, haces pasajes de términos, y queda:
-m = -x - 2, multiplicas por -1 en todos los términos de la ecuación, y queda:
m = x + 2 (2).
Luego, a fin de plantear la intersección entre la recta t y la recta r, sustituyes la expresión señalada (2) en la ecuación señalada (1), y queda:
y - 3 = (x + 2)*(x + 2), reduces factores semejantes en el segundo miembro, y queda:
y - 3 = (x + 2)2,
que es una ecuación cartesiana de una parábola con eje paralelo al eje OY, con vértice V(-2,3), con ssu ramas hacia arriba.
Espero haberte ayudado.
Antonio Silvio Palmitano
el 30/1/18Tienes la inecuación:
(x - 2)*(x2 + 4y2 - 16) ≥ 0, extraes factor común 16 en el segundo factor, y queda:
(x - 2)*16*(x2/16 + y2/4 - 1) ≥ 0,
divides por 16 en ambos miembros de la inecuación (observa que no cambia la desigualdad), y queda:
(x - 2)*(x2/16 + y2/4 - 1) ≥ 0;
luego, por anulación de un producto, tienes dos opciones (observa que el producto en el primer miembro debe ser positivo):
1)
x - 2 ≥ 0 y x2/16 + y2/4 - 1 ≥ 0, haces pasajes de términos en ambas inecuaciones, y queda:
x ≥ 2 y x2/16 + y2/4 ≥ 1;
observa que la primera inecuación corresponde a un semiplano, cuyos puntos se encuentran a la derecha de la recta cuya ecuación es x = 2, y observa que la segunda inecuación corresponde a la región exterior al disco elíptico con centro de simetría (0,0), semieje mayor horizontal: a = 4, y semieje menor vertical: b = 2, por lo que tienes el conjunto de los puntos del semiplano que son exteriores al disco elíptico, con los puntos de sus bordes pertenecientes a él;
2)
x - 2 ≤ 0 y x2/16 + y2/4 - 1 ≤ 0, haces pasajes de términos en ambas inecuaciones, y queda:
x ≤ 2 y x2/16 + y2/4 ≤ 1;
observa que la primera inecuación corresponde a un semiplano, cuyos puntos se encuentran a la izquierda de la recta cuya ecuación es x = 2, y observa que la segunda inecuación corresponde a la región interior al disco elíptico con centro de simetría (0,0), semieje mayor horizontal: a = 4, y semieje menor vertical: b = 2, por lo que tienes el conjunto de los puntos del semiplano que son interiores al disco elíptico, con los puntos de sus bordes pertenecientes a él;
luego, tienes que el conjunto solución es la unión de los dos conjuntos:
S = { (x,y) ∈ R2 / [ x ≥ 2 y x2/16 + y2/4 ≥ 1 ] o [ x ≤ 2 y x2/16 + y2/4 ≤ 1 ] },
y queda que hagas la representación gráfica.
Espero haberte ayudado.