-
Isaac Balbuca
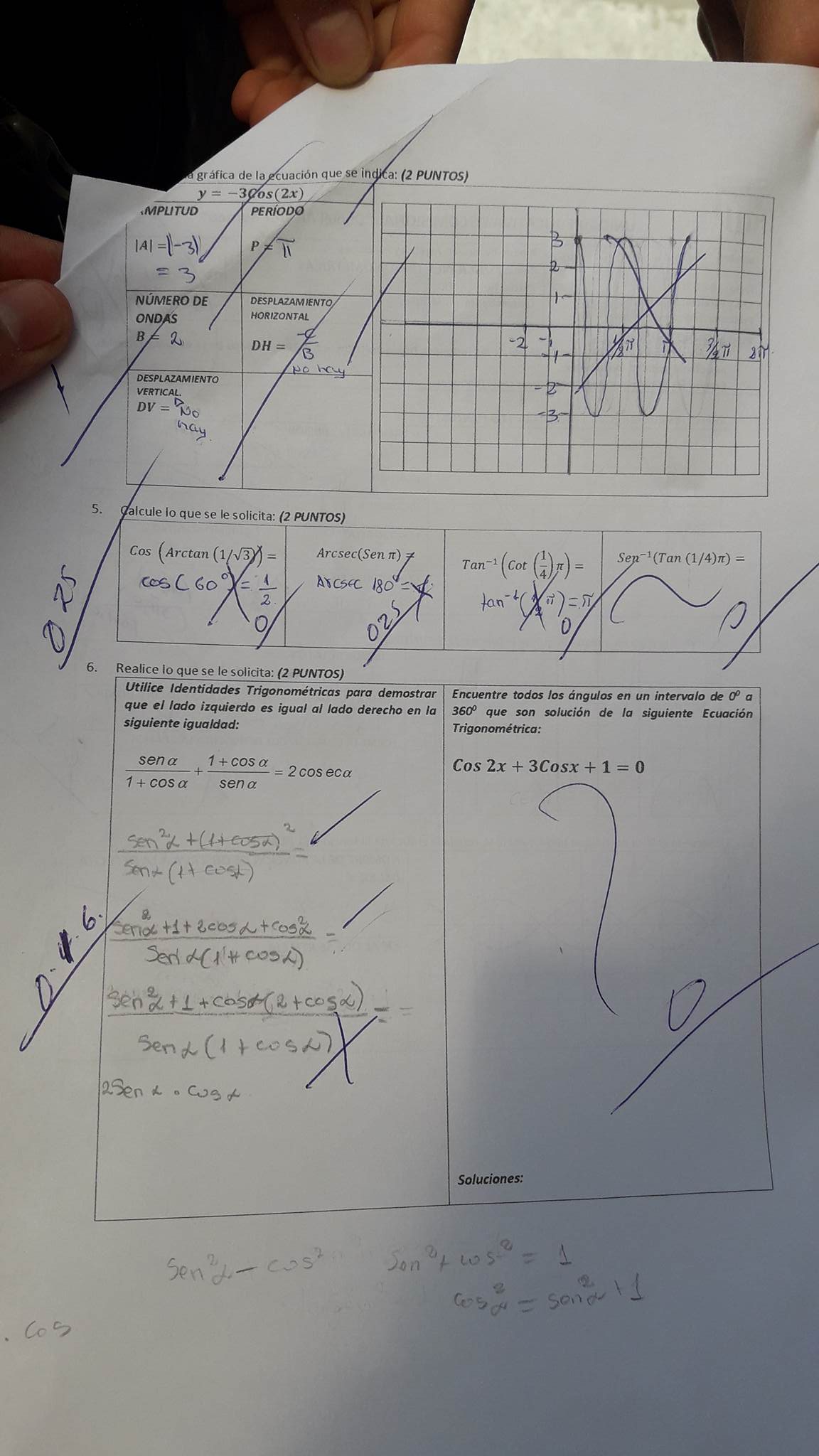
el 30/1/18Urgente ayudenme porfavor a ver como resuelvo la pregunta 5 de esta imagen porfavorr mañana me evaluan sobre esto y quiero comprender porfavooor
Ángel
el 30/1/186) a.
senx/(1+cosx) + (1+cosx)/(senx) = 2*cosecx
senx/(1+cosx) + (1+cosx)/(senx) = 2*(1/senx)
senx/(1+cosx) + (1+cosx)/(senx) = 2/(senx)
senx/(1+cosx) + (1+cosx)/(senx) = 2/(senx)
((senx)*(senx))/((1+cosx)*(senx)) + ((1+cosx)*(1+cosx))/((1+cosx)*(senx)) = (2*(1+cosx))/((1+cosx)*(senx))
((senx)*(senx)) + ((1+cosx)*(1+cosx)) = (2*(1+cosx))
sen2x + (1+cosx)2 = 2+2cosx
1-cos2x + (1+cos2x+2cosx) = 2 + 2cosx
1-cos2x + 1+cos2x+2cosx = 2 + 2cosx
2+2cosx = 2+2cosx
(2+2cosx)/(2+2cosx) = (2+2cosx)/(2+2cosx)
1=1
Ángel
el 30/1/186) b.
(cos2x) + 3cosx +1 = 0
(cos2x - sen2x) + 3cosx +1 = 0
cos2x - sen2x + 3cosx +1 = 0
cos2x - (1-cos2x) + 3cosx +1 = 0
cos2x - 1+cos2x + 3cosx +1 = 0
2cos2x+3cosx = 0
cosx*(2cosx+3)= 0
Factor 1: cosx=0 ---------> arcos(0º) = 90º y 270º
Factor 2: 2cosx+3=0 ----> cosx= -3/2 -------> No hay ninguna "x" en los números reales (y por lo tanto tampoco de 0 a 360 grados)
que haga que el cosx = -3/2, por lo tanto cosx≠ -3/2 ∀ℛ
**La solución en general es cosx= 0 ----> arcosx= 90º + 180º*n, pero si hablamos del intervalo que pide tu ejercicio las soluciones son 90º y 270º
Ángel
el 31/1/185)
cos(arctg(1/√3)) = cos(arctg((1*√3)/(√3*√3))) = cos(arctg((√3)/3)) = cos(30) = (√3)/2
arcsec(senπ)= arcsec(0º) ----> No existe, sólo existe para -1rad ≤ x ≤ 1rad https://www.symbolab.com/solver/step-by-step/arcsecx
-
David de la Torre
el 30/1/18que recomendables son para matemáticas grado en ADE?
Ángel
el 30/1/18
Parece que hay 6 asignaturas que son fundamentalmente de matemáticas (la más chunguilla parece econometría), las otras 5 son de lo que se ve en bachillerato y un poco más allá.
En la mayoría parece que se tocan muchos conceptos matemáticos, pero no se profundiza mucho, suelen ser de aplicación más o menos directa...
Esa es mi vaga y poco madurada opinión (ya que no tengo experiencia en este tipo de carreras), pero aquí tienes el planning para que lo veas tú mismo:
http://portal.uned.es/portal/page?_pageid=93,53691653&_dad=portal&_schema=PORTAL&idGrado=6502
-
Martín Sebastian
el 30/1/18 -
Gabriela
el 30/1/18
Hola unicoos necesito ayuda con el siguiente ejercicio: Probar que si dos operadores autoadjuntos T,S:V--->V conmutan, Entonces el espacio vectorial V posee una base ortonormal formada por autovectores comunes a T y S. Probar la recíproca.
Antonius Benedictus
el 30/1/18¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
Julian
el 29/1/18Me podrían ayudar con estas 2 porfa
Ángel
el 29/1/18 -
Usuario eliminado
el 29/1/18 -
Usuario eliminado
el 29/1/18 -
Silvia
el 29/1/18Hola, me podeis ayudar con este ejercicio de inecuacion con fraciones? Por favor, es URGENTE el examen lo tengo mañana. Gracias
Ángel
el 29/1/18 -
Froylan
el 29/1/18 -
Iman Mamlakti
el 29/1/18
