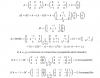A mí me sale esto. Revísalo:

Con los valores que te dan en las opciones a), c) y d) obtienes que el límite de esa función es infinito, sin embargo, si sustituyes con los valores de b) obtienes que el límite es 1 (opción correcta).

lim(x→2) ((√(x+6)-3)/(2-√(x+1))) =  ((√(2+6)-3)/(2-√(2+1))) =  (√(8)-3)/(2-√(3)) = -0.64031868764

lim(x→1) ((x-1)/(∛(x)-⁶√(x)) =   lim(x→1) ((x-1)/((x)^1/3-(x)^1/6) =    lim(x→1) ((x-1)/((x)^2/6-(x)^1/6) =  lim(x→1) ((x-1)/((x)^2/6-1/6) =  lim(x→1) ((x-1)/(x^1/6) =  (1-1)/1 = 0/1 = 0

Entonces:

lim(x→2) ((√(x+6)-3)/(2-√(x+1))) + sgn ( lim(x→1) ((x-1)/(∛(x)-⁶√(x)) ) =    -0.64031868764 + sgn ( 0 )  =  -0.64031868764 + 0  =        -0.64031868764    <----Solución

--------------

**Ten en cuenta que sgn(0)=0

https://es.wikipedia.org/wiki/Funci%C3%B3n_signo

Llevas razón... la simplificación llevó a error, corrijo entonces:

lim(x→2) ((√(x+6)-3)/(2-√(x+1))) =  ((√(2+6)-3)/(2-√(2+1))) =  (√(8)-3)/(2-√(3)) = -0.64031868764

lim(x→1) ((x-1)/(∛(x)-6√(x)) =   6

Entonces:

lim(x→2) ((√(x+6)-3)/(2-√(x+1))) + sgn ( lim(x→1) ((x-1)/(∛(x)-6√(x)) ) =    -0.64031868764 + sgn ( 6 )  =  -0.64031868764 + 1  =        0.35968    <----Solución

Sorry!

muchisimas gracias!

Para completar el a) sólo te falta calcular las frecuencias relativas f_i y con ellas calcular fácilmente las frecuencias relativas acumuladas

Para hacer el b) te conviene sumar todas las columnas en rojo, y con esos datos calcularás media, mediana, varianza y desviación stándar

¿Por qué pones "n"?

La distribución de frecuencias a las que se refiere la tabla son las absolutas (ni).

Por definición, la suma de frecuencias relativas fi da de resultado 1 ...... y obviamente 5+10+43+27+9= 94≠1

Si sigues avanzando en el ejercicio verás que llamar ni es lo correcto y toma todo su sentido, porque n1+n2+n3+n+n5=n=94 observaciones

Media=(∑ki=1xi*ni)/n = (305+640+2881+1890+657)/94 ≈ 67.8 pulgadas.

http://www.luiszegarra.cl/moodle/pluginfile.php/149/mod_resource/content/1/cap9.pdf

Aquí tienes los fundamentos teóricos que necesitas para solucionar tu problema y muchos problemas resueltos y propuestos más fáciles, de igual dificultad y más difíciles.

Después de estudiarlo intenta hacer el ejercicio de tu enunciado y si no te sale nos dices tus dudas y te ayudamos.

Gracias por el material, está muy completo.

Hay un ejercicio parecido al que formulé pero dan el centro explícitamente. En mi caso el centro está en una recta. Intenté despejando las variables x e y de la recta y sustituyéndolas en la ecuación de la circunferencia para posteriormente desarrollar los productos notables, pero no estoy muy segura si por ese camino llegaré al resultado correcto. ¿Me indicarías cómo lo solucionarías?

a)

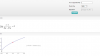
Observa que el dominio es: D = R - {-1,1}, ya que no tienes puntos en las rectas verticales que pasan por x = -1 y por x = 1.

Observa que su recorrido es: I = R (asumimos que la gráfica se acerca al eje OX tanto muy hacia la izquierda como muy hacia la derecha).

b)

Observa que la gráfica corta a ambos ejes coordenados en el origen de coordenadas.

c)

Observa que la gráfica es simétrica con respecto al eje OY, por lo que tienes que la función es par, y se cumple: f(-x) = f(x) (en forma práctica, si pliegas el gráfico tomando al eje OY como recta de plegado, tienes que las dos partes de la gráfica se superponen).

d)

Observa que la función es:

Creciente en los intervalos: (-∞,-1) y (-1,0) ("a la izquierda de x = -1, y entre x = -1 y x = 0";

Decreciente en los intervalos: (0.1) y (1,+∞) ("entre x = 0 y x = 1, y a la derecha de x = 1).

e)

Observa que la gráfica presenta un Máximo Relativo (o Local) en x = 0, y el valor de la función para él es: f(0) = 0.

Observa que la gráfica no presenta máximos absolutos, ni mínimos relativos, ni mínimos absolutos.

f)

Observa que la gráfica es Cóncava hacia Arriba en los intervalos: (-∞,-1) y (1,+∞).

Observa que la gráfica es Cóncava hacia Abajo en el intervalo: (-1,1).

Espero haberte ayudado.

1)

Plantea la expresión general de un polinomio de grado dos:

P(x) = a*x² + b*x + c (1), con los coeficientes a, b, c, que debes determinar.

Luego, evalúa la expresión del polinomio para el argumento: 2x+1, para ello sustituyes y queda:

P(2x+1) = a*(2x+1)² + b*(2x+1) + c, resuelves el binomio elevado al cuadrado, distribuyes en los dos primeros términos, y queda:

P(2x+1) = 4a*x² + 4a*x + 1 + 2b*x + 2b + c, asocias términos lineales, asocias términos constantes, ordenas términos, y queda:

P(2x+1) = 4a*x² + (4a+2b)*x + (2b+c+1) (2).

Luego, tienes la ecuación de tu enunciado:

P(2x+1) = 8*x² + 14*x, sustituyes la expresión señalada (2) en el primer miembro, sumas 0 en el segundo miembro, y queda:

4a*x² + (4a+2b)*x + (2b+c+1) = 8*x² + 14*x + 0;

luego, por igualdad entre polinomios, igualas coeficientes entre términos con grados iguales, y queda el sistema de ecuaciones:

4a = 8, aquí haces pasaje de término, y queda: a = 2,

4a + 2b = 14, aquí reemplazas el valor remarcado, haces pasaje de término, y luego de factor como divisor, y queda: b = 3,

2b + c + 1 = 0, aquí reemplazas el último valor remarcado, reduces términos semejantes, haces pasaje de término, y queda: c = -7.

Luego, reemplazas los valores remarcados en la expresión del polinomio señalada (1), y queda:

P(x) = 2*x² + 3*x - 7.

2)

a)

Tienes el polinomio:

Q(x) = x⁴ + x³ - 9*x² - 9*x, extraes factor común, y queda:

Q(x) = x*( x³ + x² - 9*x - 9 ), extraes factores comunes por grupos en el agrupamiento, y queda:

Q(x) = x*( x²*(x+1) - 9*(x+1) ), extraes factor común en el agrupamiento, y queda.

Q(x) = x*(x+1)*(x² - 9), factorizas la resta entre cuadrados perfectos en el último agrupamiento, y queda:

Q(x) = x*(x+1)*(x+3)*(x-3).

b)

Tienes la ecuación:

x⁴ + x³ - 9*x² - 9*x = 0, sustituyes la expresión remarcada en el primer miembro, y queda:

x*(x+1)*(x+3)*(x-3) = 0; luego, por anulación de un producto, anulas cada factor por separado, y tienes cuatro opciones:

x = 0;

x + 1 = 0, aquí haces pasaje de término, y queda: x = -1;

x + 3 = 0, aquí haces pasaje de término, y queda: x = -3;

x - 3 = 0, aquí haces pasaje de término, y queda: x = 3.

3)

Haces pasaje de término (observa que x debe ser distinta de -3 y de 3), y la ecuación de tu enunciado queda:

(x² - 32)/4 = -28/(x² - 9), haces pasajes de divisores como factores, y queda:

(x² - 32)*(x² - 9) = -112;

aquí planteas la sustitución (cambio de incógnita): u = x² (1) (observa que u toma valores estrictamente positivos), sustituyes y queda:

(u - 32)*(u - 9) = -112, distribuyes en el primer miembro, haces pasaje de término, reduces términos semejantes, y queda:

u² - 41*u + 400 = 0, que es una ecuación polinómica cuadrática, aplicas la Fórmula de Baskara, y sus soluciones son:

1°)

u = 16, reemplaza en la ecuación señalada (1) y queda: x² = 16, haces pasaje de potencia como raíz, y queda: x = -4 y x = 4;

2°)

u = 25, reemplaza en la ecuación señalada (1) y queda: x² = 25, haces pasaje de potencia como raíz, y queda: x = -5 y x = 5;

y luego puedes concluir que los valores remarcados son las cuatro soluciones de la ecuación de tu enunciado.

4)

Tienes el polinomio:

P(x) = 2*x³ + x² - m*x + n (1), con los coeficientes m, n que debes determinar;

luego, tienes que el polinomio es divisible por (x-3), por lo que aplicas el Teorema del Resto, y tienes la ecuación:

P(3) = 0, sustituyes la expresión evaluada del polinomio en el primer miembro, y queda:

63 - 3*m + n = 0, haces pasajes de términos, y queda:

n = 3*m - 63 (2);

luego, tienes que el resto de la división del polinomio entre el binomio (x+3) es igual a 6, por lo que aplicas el Teorema del Resto, y tienes la ecuación:

P(-3) = 6, sustituyes la expresión evaluada del polinomio en el primer miembro, y queda:

-45 + 3*m + n = 0, sustituyes la expresión señalada (2), reduces términos semejantes, y queda:

6*m - 108 = 0, haces pasaje de término, luego de factor como divisor, y queda: m = 18;

luego, reemplazas el valor remarcado en la ecuación señalada (2), resuelves y queda: n = -9;

luego, reemplazas los valores remarcadosen la expresión del polinomio señalada (1), y queda:

P(x) = 2*x³ + x² - 18*x - 9.

Espero haberte ayudado.

Observa que dices que la sucesión es geométrica, pero hablas de diferencia (que corresponde a sucesiones aritméticas) en lugar de razón (que corresponde a sucesiones geométricas), por lo que debes verificar tu enunciado.

A modo de orientación, vamos con los dos casos.

a)

Si la sucesión es geométrica (recuerda la expresión de su elemento general: a_n = a₁*r^n-1), tienes los datos: 

a₁ = 1 (primer elemento), r = 2 (razón), n = 10 (número de orden del último elemento);

luego, plantea la sucesión de sumas parciales:

S₁ = a₁ = a₁*(1-r¹)/(1-r),

S₂ = a₁ + a₂ = a₁ + a₁*r = a₁*(1+r) = a₁*(1+r)*(1-r)/(1-r) = a₁*(1-r²)/(1-r),

S₃ = a₁ + a₂ + a₃ = a₁ + a₁*r + a₁*r² = a₁*(1+r+ r²) = a₁*(1+r+r²)*(1-r)/(1-r) = a₁*(1-r³)/(1-r),

S₄ = a₁ + a₂ + a₃ + a₄ = a₁ + a₁*r + a₁*r² + a₁*r³ = a₁*(1+r+ r²+r³) = a₁*(1+r+r²+r³)*(1-r)/(1-r) = a₁*(1-r⁴)/(1-r),

luego, puedes inferir (y demostrar con el Principio de Inducción Completa), que la expresión de la suma parcial general es:

S_n = a₁*(1-rⁿ)/(1-r);

luego, reemplazas los datos de tu enunciado, y queda:

S₁₀ = 1*(1-2¹⁰)/(1-2) = 1*(1-1024)/(-1) = 1*(-1023)/(-1) = 1023.

b)

Si la sucesión es aritmética (recuerda la expresión de su elemento general: a_n = a₁+(n-1)*d), tienes los datos: 

a₁ = 1 (primer elemento), d = 2 (diferencia), n = 10 (número de orden del último elemento);

luego, plantea la suma de los diez primeros elementos:

S₁₀ = a₁ + a₂ + a₃ + a₄ + a₅ + a₆ + a₇ + a₈ + a₉ + a₁₀;

luego, ordenas y asocias términos, y queda:

S₁₀ = (a₁ + a₁₀) + (a₂ + a₉) + (a₃ + a₈) + (a₄ + a₇) + (a₅+a₆);

luego, sustituyes las expresiones de los elementos en los agrupamientos, y queda:

S₁₀ = (a₁ + a₁+9*d) + (a₁+1*d + a₁+8*d) + (a₁+2*d + a₁+7*d) + (a₁+3*d + a₁+6*d) + (a₁+4*d+a₁+5*d);

luego, reduces términos semejantes en los agrupamientos, y queda:

S₁₀ = (a₁+a₁+9*d) + (a₁+a₁+9*d) + (a₁+a₁+9*d) + (a₁+a₁+9*d) + (a₁+a₁+9*d);

luego, reduces términos semejantes, y queda:

S₁₀ = (a₁+a₁+9*d)*5;

luego, sustituyes la expresión remarcada (observa que tienes: a₁₀ = a₁+9*d), expresas al factor numérico como la mitad de su doble, y queda:

S₁₀ = (a₁ + a₁₀)*10/2,

que es un caso particular de la expresión de la suma parcial de los n primeros elementos de una sucesión aritmética: S_n = (a₁+a_n)*n/2;

luego, reemplazas los datos que tienes en u enunciado, y queda:

S₁₀ = (a₁ + a₁₀)*10/2 = (a₁ + a₁+9*d)*10/2 = (1 + 1+9*2)*10/2 = 20*5 = 100.

Espero haberte ayudado.

¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que  lo entiendas.

Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).