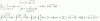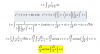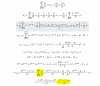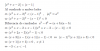-
Antonio Silvio Palmitano
el 28/1/18Debes corregir en la expresión de la función:
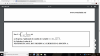
f(x) = |10 - 5*x| - 2*x =
10 - 5*x - 2*x si 10 - 5*x ≥ 0 (*)
-10 + 5*x - 2*x si 10 - 5*x < 0 (**);
luego, observa que si haces pasajes de términos en las inecuaciones señaladas (*) (**) quedan:
-5*x ≥ -10, haces pasaje de factor como divisor (observa que cambia la desigualdad), y queda: x ≤ 2;
-5*x < -10, haces pasaje de factor como divisor (observa que cambia la desigualdad), y queda: x > 2.;
luego, tienes que la expresión de la función queda:
f(x) = |10 - 5*x| =
10 - 7*x si x ≤ 2
-10 + 3*x si x > 2.
Luego, tienes la integral:
I = 1∫3 (|10 - 5*x| - 2*x)*dx, descompones como suma de integrales, y queda:
I = 1∫2 (|10 - 5*x| - 2*x)*dx + 2∫3 (|10 - 5*x| - 2*x)*dx, sustituyes expresiones en los argumentos de las integrales, y queda:
I = 1∫2 (10 - 7*x)*dx + 2∫3 (-10 + 3*x)*dx;
luego, integras en ambos términos (observa que indicamos con corchetes que debes evaluar con Regla de Barrow), y queda:
I = [ 10*x - (7/2)*x2 ] + [ -10*x + (3/2)*x2 ];
luego, evalúas en cada término según sus límites de integración, y queda:
I = ( (20-14) - (10-7/2) ) + ( (-30+27/2) - (-20+6) ), resuelves agrupamientos menores, y queda:
I = (6 - 13/2) + (-33/2 + 14), resuelves agrupamientos, y queda:
I = -1/2 - 5/2 = -6/2 = -3.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 28/1/18a)
Te indican en tu enunciado que plantees el cambio de variable:
t = 2 + √(x+1) (*), haces pasaje de término, y queda:
t - 2 = √(x+1) (1), haces pasaje de raíz como potencia, y queda:
(t - 2)2 = x + 1, haces pasaje de término, y queda:
(t - 2)2 - 1 = x, y a partir de aquí tienes:
2*(t - 2)*dt = dx (2).
Luego, sustituyes las expresiones señaladas (1) (2), y la integral de tu enunciado queda (observa que dejamos expresados los límites de integración):
I = a∫b (1/t)*2*(t - 2)*dt, distribuyes en el argumento, y queda:
I = a∫b (2 - 4/t)*dt, integras (observa que indicamos con corchetes que debes evaluar con Regla de Barrow), y quda:
I = [ 2*t - 4*ln|t| ];
luego, sustituyes la expresión señalada (*) (observa que recuperas los límites de integración de tu enunciado, y queda:
I = [ 2*( 2 + √(x+1) ) - 4*ln|2 + √(x+1)| ];
luego, evalúas con Regla de Barrow entre x = 0 y x = 8, y queda:
I = ( 2*5 - 4*ln(5) ) - ( 2*3 - 4*ln(3) ), resuelves en los dos términos, y queda:
I = 10 - 4*ln(5) - 6 + 4*ln(3), reduces términos semejantes, y queda:
I = 4 - 4*ln(5) + 4*ln(3).
Espero haberte ayudado.
-
Doce trabajadores pueden hacer una obra en 160 días ¿qué tiempo necesitarán 4 obreros del mismo rendimiento para realizar la misma labor?
Antonio Silvio Palmitano
el 28/1/18Observa que las magnitudes "cantidad de trabajadores (x)" y "tiempo empleado para realizar la tarea (t)" son inversamente proporcionales.
Observa que en la situación inicial y en la situación final tienes que el trabajo realizado es el mismo: una obra.
Luego, tienes los valores iniciales: xi = 12 trabajadores, ti = 160 días.
Luego, tienes los valores finales: xf = 4 trabajadores, tf = a determinar.
Luego, puedes plantear la ecuación proporcional correspondiente para magnitudes inversamente proporcionales:
xi/xf = tf/ti, reemplazas valores, y queda:
12/4 = tf/160, resuelves el primer miembro, haces pasaje de término, resuelves, y queda:
480 días = tf, que es el tiempo que tardarán 4 obreros para realizar la obra.
Espero haberte ayudado.
-
Buenas, en este video de Unicoos https://www.youtube.com/watch?v=wGl-E5LRvac se explican los cambios de base por medio de combinaciones lineales, pero en otros he visto que se hace con la matriz asociada. ¿Qué diferencia hay entre ambos métodos? Gracias de antemano
-
Explicacion números combinados naturales .
Richie
el 28/1/18David
el 31/1/18Sin un enunciado concreto es imposible saber que necesitas. Espero te sirvan estos..
Operaciones combinadas 01 -
¿Me ayudarían con esta inecuación con valor absoluto? |x^2+x-2|-|1-x|<0
Intenté pasar -|1-x|al otro lado de la desigualdad y elevar ambos miembros al cuadrado pero no puedo llegar a la solución. Por lo que para hacer más cómoda la resolución, factoricé x^2+x-2 -> | (x+2)(x-1) | y por propiedad lo separé de esta forma |x+2| |x-1| - |1-x|< 0. Sin embargo, eso me obliga a definir 3 veces y me daría tres casos con 3 inecuaciones y me es confuso. Agradecería que me ayudasen.
-
Hola buenas, el planteamiento de este problema sería así?
Una empresa invierte 2 millones de euros en un producto financiero A, 4 millones en otro B y 2 millones en C, obteniendo una rentabilidad media total del 3.5 %. Calcula la rentabilidad de estos 3 productos si el producto A renta un punto mas que el B, y que el C es tan rentable como los otros dos juntos.

Antonio Silvio Palmitano
el 28/1/18Tienes que el capital total invertido es: C = 2 + 4 + 2 = 8 millones de euros, y que la renta total obtenida es:
R = (3,5/100)*8 = 0,035*8 = 0,28 millones de euros = 280000 euros.
Luego, puedes llamar rB = r/100 a la tasa correspondiente a la inversión B, por lo que tienes que la tasa correspondiente a la inversión A es rB = (r+1)/100, y que la tasa correspondiente a la inversión C es rC = (r + r+1)/100 = (2*r+1)/100.
Luego, plantea la expresión de interés simple (I = C*(r/100)*t) para cada una de las rentas de las inversiones (suponemos que el tiempo es igual a un periodo de capitalización):
RA = CA*rA*t = 2*( (r+1)/100 )*1 = (2*r + 2)/100 (1) (en millones de euros),
RB = CB*rB*t = 4*( r/100 )*1 = 4*r/100 (2) (en millones de euros),
RC = CC*rC*t = 2*( (2*r+1)/100 )*1 = (4*r + 2)/100 (3) (en millones de euros).
Luego, tienes para la renta total obtenida:
RA + RB + RC = R, sustituyes las expresiones señaladas (1) (2) (3) y el valor de la renta total, y queda:
(2*r + 2)/100 + 4*r/100 + (4*r + 2)/100 = 0,28, multiplicas por 100 en todos los términos de la ecuación, y queda:
2*r + 2 + 4*r + 4*r + 2 = 28, haces pasajes de términos, reduces términos semejantes, y queda:
10*r = 24, haces pasaje de factor como divisor, y queda:
r = 2,4;
luego, reemplazas en las expresiones señaladas (1) (2) (3), y queda:
RA = 0,068 millones de euros = 68000 euros,
RB = 0,096 millones de euros = 96000 euros,
RC = 0,116 millones de euros = 116000 euros,
y observa que las tasas de rendimiento de las inversiones son:
rA = 3,4 %, rB = 2,4 %, rC = 5,8 %.
Espero haberte ayudado.
-
Buenas noches me pueden ayudar con estos ejercicios no soy capaz de resolver.
Muchas gracias
Sabiendo que log k = 14,4, calcula el valor de las siguientes expresiones:
Antonio
el 27/1/18Antonio Silvio Palmitano
el 28/1/18Vamos con una precisión.
Debes tener en cuenta las propiedades de los logaritmos:
log(x*y) = log(x) + log(y),
log(x/y) = log8x) - log(y),
log(xp) = p*log(x),
log( r√(x) ) = (1/r)*log(x),
log(10) = 1,
log(1) = 0.
Luego, si consideramos que los logaritmos de tu enunciado son decimales, aplicas las propiedades correspondientes en cada paso, y tienes:
a)
log(k/100) = log(k) - log(100) = log(k) - log(102) = log(k) - 2*log(10) = reemplazas valores = 14,4 - 2*1 = 14,4 - 2 = 12,4.
b)
log(0,1*k2) = log(0,1) + log(k2) = log(1/10) + 2*log(k) = log(1) - log(10) + 2*log(k) = reemplazas valores = 0 - 1 + 2*14,4 = -1 + 28,8 = 27,8.
c)
log(∛(1/k) = (1/3)*log(1/k) = (1/3)*( log(1) - log(k) ) = reemplazas valores = (1/3)*(0 - 14,4) = (1/3)*(-14,4) = - 4,8.
d)
( log(k) )1/2 = expresas a la potencia fraccionaria como raíz = √( log(k) ) = reemplazas = √(14,4) = √(144*10/100) = √(144)*√(10)/√(100) = 12*√(10)/10 = 6*√(10)/5.
Espero haberte ayudado.