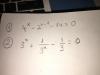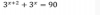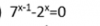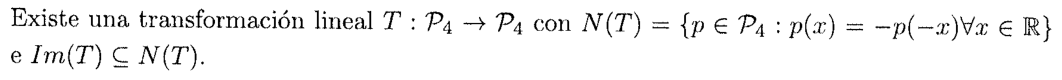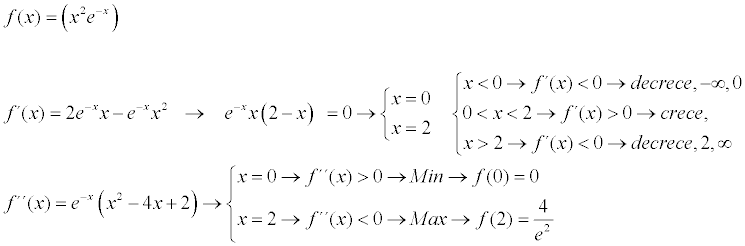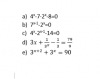Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

Mathias
el 26/1/18

_{Viendo el Teorema de las disensiones, ¿una transformación lineal siempre que es sobreyectiva también es inyectiva (y al revés)?}

••0 voto/s
•
Ángel
el 27/1/18
Si nos rediriges a un link con información acerca del "Teorema de las disensiones", quizá podamos ayudarte. Yo no he encontrado nada respecto a este tema.

•1 voto/s
•
Antonius Benedictus
el 27/1/18
No, Mathías. Esto sucede solamente cuando la transformación lineal va de un espacio en otro de la misma dimensión ( o en el mismo espacio, y se trata de un endomorfismo).
Si dim(E)=n y dim (F)=m
n>m obliga a que no sea inyectiva.
n<m obliga a que no sea sobreyectiva.

•1 voto/s
•
Mathias
el 27/1/18
Para Ángel:

•0 voto/s
•
Ángel
el 27/1/18
"Teorema de las diSensiones" ≠ TEOREMA (de las diMensiones)

•0 voto/s
•

Cancelar
SODA
el 26/1/18

¿Me ayudan con esto?
Hallar la ecuación de una recta que es perpendicular a 5x+8y=13 y que contiene al punto (Xo, Yo) que está en la recta y=x

••1 voto/s
•
Antonio Silvio Palmitano
el 26/1/18
Plantea la ecuación explícita de la primera recta, para ellos haces pasaje de término, y queda:
8y = -5x + 13, luego divides por 8 en todos los términos de la ecuación, y queda: y = -(5/8)x + 13/8,
y observa que su pendiente es: m = -5/8.
Luego, tienes que el punto indicado pertenece a la recta cuya ecuación es y = x, por lo que sus coordenadas son: (x₀,x₀).
Luego, tienes que la pendiente de la recta buscada, que es perpendicular a la primera recta queda: M = -1/m = -1/(-5/8) = 8/5.
Luego, planteas la expresión de la ecuación punto-pendiente de la recta buscada y queda:
y = M*(x - x₀) + x₀, reemplazas el valor de la pendiente, y queda:
y = (8/5)*(x - x₀) + x₀, distribuyes el primer término, reduces términos semejantes, y queda:
y = (8/5)x - (3/5)x₀,
que es la ecuación de un conjunto de rectas que cumplen las condiciones que tienes en tu enunciado.
Espero haberte ayudado.

•0 voto/s
•

Cancelar
Luis Ortega
el 26/1/18

Como se haria esto? Me lo pueden explicar paso a pso? Gracias de antemano

••0 voto/s
•
Mathias
el 26/1/18
Fijate las propiedades de potencia:
https://www.vitutor.net/1/potencias.html
Usando esas cosas, sacas factor común, pon las potencias de un lado y el resto del otro y aplica la definición de logaritmo.

•0 voto/s
•
Mathias
el 26/1/18
en donde dice 4^x tené en cuenta que lo podés escribir como (2^2)^x

•0 voto/s
•

Cancelar
Adela García
el 26/1/18

Me podeis ayudar con estos ejercicios:?:
1)
2)

••0 voto/s
•
Mathias
el 26/1/18
En el 1, sacas como factor común el 3^x y te queda el 3^x(3^2 +1), dejas el que está con la potencia de un lado y lo que son solo números del otro. Ahí aplicas la definición de logaritmo. El 2do es igual

•0 voto/s
•
Ángel
el 27/1/18
2)
7x-1-2x= 0
7x-1= 2x
ln(7x-1) = ln(2x)
(x-1)*ln7 = ln(2x)
ln7*x-ln7 = x*ln2
ln7*x- x*ln2 = ln7
x= (ln7)/(ln7-ln2)
x= (ln7)/(ln(7/2))

•0 voto/s
•
Ángel
el 27/1/18
1)
3^x+2+3^x=90
Cambio de variable t=3x
t²+t=90
t²+t-90=0
Resuelves y obtienes:
t1=9
t2= -10

Como t1=3^x=9=3², entonces x=2
Como t2=3^x= -10, entonces no existe solución en R.

https://www.unicoos.com/video/matematicas/4-eso/ecuaciones-y-sistemas/ecuaciones-exponenciales-y-logaritmicas/ecuacion-exponencial-de-segundo-grado

•0 voto/s
•

Cancelar
Mathias
el 26/1/18

Buenas, como podría saber si existe una transformación lineal tal que dado el núcleo, la imagen de ésta esté incluida en su núcleo. Dejo captura de la pregunta (es un verdadero o falso):

Gracias.
••0 voto/s
•
Antonius Benedictus
el 27/1/18

•1 voto/s
•

Cancelar
Ylenia Montes
el 26/1/18

Tengo una pregunta. Si a z le doy el valor de lambda, ¿porque no le da valor para t otro valor también? Muchas gracias

••0 voto/s
•
Antonius Benedictus
el 26/1/18
Pon foto del enunciado original.

•0 voto/s
•

Cancelar
Majda Yahya
el 26/1/18

Necesito ayuda con esta actividad, he podido derivarla pero no estoy segura del resultado de mínimos y máximos que me ha dado, ¿alguien me ayuda?

••0 voto/s
•
César
el 26/1/18

•1 voto/s
•
Antonius Benedictus
el 26/1/18

•2 voto/s
•

Cancelar
Iman Mamlakti
el 26/1/18

Me podría ayudar con estas ecuaciones por favor

••0 voto/s
•
Antonius Benedictus
el 26/1/18
Has puesto las posibles soluciones, no el enunciado.

•0 voto/s
•

Cancelar
Usuario eliminado
el 26/1/18

Te dan una superficie. En este caso un hiperboloide de una hoja:
(x-1)^2-4*(y-2)^2+z^2=9
En este ejercicio me piden hallar los planos tangentes en varios puntos. Decir si se puede despejar de forma implicita z=(xy) y a parte encontrar los puntos críticos.
Mi pregunta es El vector gradiente que es el que tengo que utilizar para todos los ejercicios ( tanto el de planos tangentes como el de puntos criticos) puedo expresarlo como:
Δf(xyz)=(2x-2,8y-16,2z)
ó tendría que despejar z : z=f(xy)= raiz de 9+4(y-2)^2-(x-1)^2 y de ahi sacar el gradiente y luego las derivadas de segundo orden (lo cual es algo más complicado)
En resumen...¿ da igual de dónde lo saque?¿ puedo hacerlo de la primera forma que es mucho más sencilla o no? y por qué?
Gracias

••0 voto/s
•
César
el 26/1/18

•1 voto/s
•
Usuario eliminado
el 26/1/18
Muchísimas gracias! Me ha quedado más claro.
Pero, ¿la forma implícita de F(xyz)=0 no es z= f(xy)?

•0 voto/s
•
César
el 26/1/18
esa es explícita.

•1 voto/s
•

Cancelar
Lucia Serrano
el 26/1/18

Me podeis explicar estos ejercicios. Tengo examen y no tengo ni idea. Mil gracias

••0 voto/s
•
Ángel
el 26/1/18
Son ejercicios en los que has de aplicar cambio de variable y la fórmula para ecuaciones de segundo grado.
a)
Cambio de variable t=2^x
t²-7t-8 = 0
Aplicas la fórmula y obtienes:
t1= -1
t2= 8

Deshacemos cambio de variable:
t1= -1 = 2^x -----> No existe solución en ℛ
t2= 8 = 2^x -----> x=3

•0 voto/s
•
Ángel
el 26/1/18
b)
7^x-1-2^x= 0
7^x-1=2^x
ln(7^x-1) = ln(2^x)
(x-1)*ln7 = ln(2^x)
ln7*x-ln7 = x*ln2
ln7*x- x*ln2 = ln7
x= (ln7)/(ln7-ln2)
x= (ln7)/(ln(7/2))

•0 voto/s
•
Ángel
el 26/1/18
c)
Se hace igual que el a) y obtienes como solución no válida x= -7/2 y la válida x=2

d)
Tu enunciado tiene un fallo, debería ser 3^x + (1/3^x) - 1/3 = 0
Cambio de variable t=3^x
Obtienes x1= -2 , x2= 2

e)
Cambio de variable t=3^x
Obtienes x=2

•0 voto/s
•
Lucia Serrano
el 26/1/18
Deshacemos cambio de variable:
t1= -1 = 2^x -----> No existe solución en ℛ
t2= 8 = 2^x -----> x=3

Y eso como se hace? de donde sale el x=3?

•0 voto/s
•
Ángel
el 27/1/18
t1= -1 = 2x -----> Como no hay ningún número en los reales que, con base 2, pueda dar de resultado -1, entonces No existe solución en ℛ

Ten en cuenta que 2³=8 ...
t2= 8 = 2x -----> t2= 2³ = 2^x -----> x=3

--------------------
https://www.unicoos.com/video/matematicas/4-eso/ecuaciones-y-sistemas/ecuaciones-exponenciales-y-logaritmicas/ecuacion-exponencial-de-segundo-grado

•0 voto/s
•

Cancelar