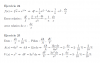-
Ylenia Montes
el 25/1/18 -
Bryam Maldonado
el 25/1/18
Me pueden ayudar con este ejercicio porfavor
Antonio Silvio Palmitano
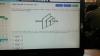
el 25/1/18Tienes que el área de cada placa mide 0,25 = 25/100 = 1/4 más que el área de la placa anterior, a partir de la segunda placa.
Tienes que las áreas miden:
A1 = 1 = (5/4)0,
A2 = 1*(1 + 1/4) = 1*5/4 = 5/4 = (5/4)1,
A3 = (5/4)1*(1 + 1/4) = (5/4)1*(5/4) = (5/4)2,
A4 = (5/4)2*(1 + 1/4) = (5/4)2*(5/4) = (5/4)3,
luego puedes inferir la expresión general del área de una placa:
Ak = (5/4)k-1,
que es la expresión del elemento general de una progresión geométrica cuyo primer elemento es: A1 = 1, y cuya razón es: r = 5/4;
y recuerda que la expresión general de la suma de los n primeros elementos de esta progresión tiene la expresión:
Sn = A1*(1 - rn)/(1 - r),
reemplazas valores (n = 10, A1 = 1, r = 5/4), y queda:
S10 = 1*(1 - (5/4)10)/(1 - 5/4) = (1 - (5/4)10)/(-1/4),
multiplicas por -1 en el numerador y en el denominador distribuyes en el numerador, y queda:
S10 = (-1 + (5/4)10)/(1/4),
ordenas términos en el numerador, y queda:
S10 = ( (5/4)10 - 1 )/(1/4),
resuelves la división, y queda:
S10 = ( (5/4)10 - 1 )*4,
ordenas factores, y queda:
S10 = 4*( (5/4)10 - 1 ),
por lo que tienes que la tercera opción es la respuesta correcta.
Espero haberte ayudado.
-
Marco Antonio
el 25/1/18 -
Daniel Albarenga
el 25/1/18Hola, buenas a todos, ando necesitando una ayudita en Álgebra, en el punto 2 quisiera saber si hay una forma de saber si el sistema es SCD (Sistema compatible determinado), SCI(Sistema compatible indeterminado) o SI(Sistema incompatible) con solo verlo?
Y en el punto 3 de igual manera, como saber sin realizar calculo alguno si una matriz aumentada tiene solución única, infinitas soluciones o ninguna??
Saludos desde Argentina!!!
Muchas gracias ..
Antonio Silvio Palmitano
el 25/1/18Hay que tener mucha práctica para determinar la compatibilidad de un sistema de ecuaciones a simple vista, en la mayoría de los casos.
Es muy evidente cuando tienes que una ecuación es múltiplo escalar de otra, o cuando una ecuación es suma o resta entre otras, pero se complica cuando tienes una combinación lineal, que es cuando una ecuación es suma o resta entre múltiplos de otras ecuaciones.
Luego, recuerda que los sistemas homogéneos siempre son compatibles porque admiten al menos la solución trivial nula, pero pueden ser determinados o indeterminados.
Por todo, lo más seguro es aplicar el Método de Gauss, y determinar el rango de la matriz y el rango de la matriz ampliada, para luego aplicar el Teorema de Rouché-Frobenius.
Por ejemplo, en el ejercicio 3a tienes que la matriz del sistema es triangular inferior, por lo que su determinante es distinto de cero y su rango es 3, y como el sistema tiene tres ecuaciones con tres incógnitas, tienes que es compatible determinado.
Por ejemplo, en el ejercicio 3d tienes que la tercera fila es igual a la suma de las otras dos filas, por lo que el sistema es compatible indeterminado, ya que la primera fila no es múltiplo de la segunda.
En los demás casos, es aconsejable que emplees el Método de Gauss antes de responder.
Espero haberte ayudado.
-
Ramon Barcelo
el 25/1/18Hola, buenas. Ciertamente este es un ejercicio complicado , tenemos que implementar el algoritmo de Knuth-Morris-Pratt (KMP) pero para cadenas en el alfabeto binario. Esta es una explicación del algoritmo:
"Este algoritmo está basado en la construcción de un AFD. El algoritmo KMP es un algoritmo de búsqueda de subcadenas simple y por lo tanto su objetivo es buscar la existencia de una subcadena dentro de una cadena. Para ello utiliza información basada en los fallos previos, aprovechando la información que la propia palabra a buscar contiene de sí (sobre ella se precalcula una tabla de valores), para determinar donde podría darse la siguiente existencia, sin necesidad de analizar más de 1 vez los caracteres de la cadena donde se busca.
El algoritmo KMP, trata de localizar la posición de comienzo de una cadena, dentro de otra. Antes que nada con la cadena a localizar se precalcula una tabla de saltos (conocida como tabla de fallos) que después al examinar entre si las cadenas se utiliza para hacer saltos cuando se localiza un fallo"
Estoy comenzando a leer este artículo: https://users.dcc.uchile.cl/~bebustos/apuntes/cc30a/BusqTexto/#2]https://users.dcc.uchile.cl/~bebustos/apuntes/cc30a/BusqTexto/#2 donde muestra el algoritmo pero para localizar búsqueda en texto, la idea es la misma pero dentro del alfabeto binario, tomando en cuenta esta página donde se muestra:
https://es.convertbinary.com/alfabeto/]https://es.convertbinary.com/alfabeto/
No pido que se me resuelta el ejercicio, solo ocupo un impulso, la idea de cómo comenzar a realizarlo, tener ideas de cómo podría ser para poder trabajar en él, la verdad es que no he logrado comprender cómo resolverlo...espero alguien pueda tomarse el tiempo.
Un saludo !.
Ángel
el 25/1/18Para que aproveches más la ayuda y orientar un poco más sobre lo que quieres, deberías ponerte en serio con el algoritmo e intentar comprenderlo....te vas apuntando las dudas concretas que te surjan (utilización de bucles, transcripciones, funcionamiento, programación, etc) y las pones aquí.
**Si escribes tus dudas te ayudaré como excepción, pero recuerda que este foro es de matemáticas.
Ramon Barcelo
el 25/1/18Hola, muchas gracias por responder.
Es muy complicado, tengo más de una semana intentando entender o intentando aplicar el algoritmo en el alfabeto binario pero me es imposible, no logro entender cómo puedo moverme de posiciones entre el 0 y 1 diferenciando las palabras. Aplicándolo en una cadena de texto convencional el procedimiento del algoritmo ya lo tengo, el cambio a binario es lo que no puedo lograr.
-
Sergi Raga Estruch
el 24/1/18
Me da 5490
Antonio Silvio Palmitano
el 25/1/18Puedes plantear para los capitales iniciales, expresados en euros:
Ci = C1 + C2. con C1 = 1000 y C2 = 4000.
Luego, puedes plantear para los capitales finales, expresados en euros:
C1f = C1*(1 + 0,08)2 = 1000*1,082 = 1000*1,1664 = 1166,4,
C2f = C2*(1 + 0,04)2 = 4000*1,042 = 4000*1,0816 = 4326,4,
y el capital final total queda:
Cf = C1f + C2f = 5492,80 euros.
Espero haberte ayudado.
-
A. Q Torres
el 24/1/18Unicoos tengo una pequeña duda con este ejercicio:
Luego que tengo la solución por cramer del determinante |Ax|y|Ay| que número utilizo para dividir por el determinante de A? . (No se si esta bien así?)
Por favor díganme si esta bien planteado el ejercicio!! Saludos y muchas gracias
Última cosa en la parte del SCI no se si es necesario hacer el rango las dos veces?
-
Ainhoa Ramos
el 24/1/18PREGUNTA NO RELACIONADA CON LAS MATES:
Hola, es que hace poco que tengo el programa de Unicoos Pro y tengo algunas dudillas. En el chat, las personas que me aparecen conectadas, ¿Son todas del mismo curso que yo o son todos los alumnos que hay metidos en esta página? Es que no se como usarlo ni si preguntarle a alguien así al azar.
Lo mismo me pasa con el foro, es solo mi curso o todo?
-
Anna Lopez
el 24/1/18Hola! Me podéis ayudar a resolver esta ecuación trigonométrica?
Sen x+sen 2x+sen 3x=0
Muchas gracias
Ángel
el 24/1/18senx + sen(2x) + sen(3x) = 0
senx + sen(2x) + sen(2x+x) = 0
senx + 2*senx*cosx + sen(2x) *cosx+ cos(2x) *senx = 0
senx + 2*senx*cosx + 2*senx*cosx *cosx+ cos2x -sen2x *senx = 0
senx + 2*senx*cosx + 2*senx*cos2x+ (1-sen2x) -sen2x *senx = 0
senx + 2*senx*√(1-sen2x) + 2*senx*(1-sen2x)+ (1-sen2x) -sen2x *senx = 0
senx + 2*senx*√(1-sen2x) + 2*(senx-sen3x)+ 1-sen2x -sen3x = 0
senx + 2*senx*√(1-sen2x) + 2*(senx-sen3x) + 1-sen2x -sen3x = 0
senx + 2*senx*√(1-sen2x) + 2senx - 2sen3x + 1-sen2x -sen3x = 0
2*senx*√(1-sen2x) = 2sen3x + sen3x + sen2x -2senx - senx
2*senx*√(1-sen2x) = 3sen3x + sen2x -3senx
2*√(1-sen2x) = 3sen2x + senx - 3
(2*√(1-sen2x))2 = (3sen2x + senx - 3)2Cambio de variable--> senx=t(2*√(1-t2))2 = (3t2 + t - 3)222*(1-t2) = 9t4 + t2 + 9 + 6t3 + 18t2 + 6t4-4t2 = 9t4 + t2 + 9 + 6t3 + 18t2 + 6t9t4 + 6t3 + 23t2 + 6t - 5 = 0Busca los valores de t del polinomio en negrita, luego deshace el cambio de variable t=senx , después calculas en arcoseno de los distintos valores x, por último combina las soluciones de x .
-
Sergi Raga Estruch
el 24/1/18
Me lo podéis resolver, gracias 
Ángel
el 24/1/18Sergi, en estos ejercicios sólo tienes que prestar un poco de atención (podrías tomar como costumbre enviar tus soluciones)
a)
temporadaPasada= x
estaTemporada= 20 = (1-0.2)*x = 0.8x
20=0.8x ----> x= 20/(0.8) = 25 = temporadaPasada
b)
Primera rebaja= 30*(1-0.2)= 30*0.8 = 24 euros
Segunda rebaja = Precio final = 24*(1-0.3) = 24*(0.7) = 16.8 euros
