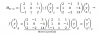Recuerda que el producto vectorial entre los vectores BC y CA es igual a un vector w, y w es perpendicular a los dos vectores a la vez, por lo que es un vector normal al plano que contiene a dichos vectores

w = BC x CA = < -1 , -8 , -6 > x < -2 , 6 , 0 > = < 36 , 12 , -22 > (1).

Luego, puedes plantear el producto vectorial entre el vector w y uno de los vectores de tu enunciado (por ejemplo: CA), y tendrás un vector p perpendicular al vector w, por lo que p pertenece al plano al que pertenecen los vectores de tu enunciado:

p = w x CA = < 36 , 12 , -22 > x < -2 , 6 , 0 > = < 132 , 44 , 240 >.

Luego, puedes plantear el producto mixto entre los vectores de tu enunciado y el vector p, a fin de verificar que los tres vectores son coplanares:

(BC x CA) • p = sustituyes la expresión señalada (1) y la expresión remarcada:

= < 36 , 12 , -22 > • < 132 , 44 , 240 > = desarrollas el producto escalar:

= 36*132 + 12*44 - 22*240 = resuelves términos:

= 4752 + 528 - 5280 = 0,

por lo que tienes que los vectores BC, CA y p son coplanares.

Espero haberte ayudado.

Muchas gracias profe. Buen día. 

Recuerda las expresiones del volumen y del área lateral para un cilindro circular recto, con radio r y altura h, y la asignas al cilindro menor:

V_m = π*r²*h (1)

A_m = 2*π*r*h (2).

Luego, como los cilindros son semejantes, puedes plantear que sus radios y sus alturas son proporcionales, por lo que puedes expresar al radio del cilindro mayor con r_M = k*r, y a su altura con h_M = k*h, donde k es la constante de proporcionalidad, que debe ser un número real estrictamente mayor que cero, y las expresiones del volumen y del área lateral para el cilindro mayor quedan:

V_M = π*(k*r)²*(k*h) = π*k²*r²*k*h = k³*π*r²*h (3),

A_M = 2*π*(k*r)*(k*h) = k²*2*π*r*h (4).

Luego, sustituyes la expresión señalada (1) en la ecuación señalada (3), sustituyes la expresión señalada (2) en la ecuación señalada (4), y queda:

V_M = k³*V_m (5),

A_M = k²*A_m (6).

a)

Reemplazas los valores que tienes en tu enunciado en las ecuaciones señaladas (5) (6), y queda:

270 = k³*80, aquí haces pasaje de factor como divisor, y luego de potencia como raíz, y queda: 3/2 = k,

A_M = k²*112, 

luego reemplazas en la segunda ecuación, y queda:

A_M = (3/2)²*112 = (9/4)*112 = 252 cm², que es el valor del área del cilindro mayor.

b)

Plantea la relación entre las alturas de los cilindros:

h_M = k*h, remplazas el valor que tienes en tu enunciado, y el valor de la constante de proporcionalidad, y queda:

6,6 = (3/2)*h, multiplicas en ambos miembros por 2/3, y queda:

4,4 cm = h, que es el valor de la altura del cilindro menor.

Espero haberte ayudado.

¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que  lo entiendas.

Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).

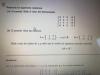
Comienza por resolver cada miembro por separado (recuerda cómo se desarrolla un producto de matrices):

A*B = 

2x-4        x-2

-4-2y      -2-y.

B² = B*B =

 2          1

-2        -1.

Luego, por igualdad entre matrices, igualas elemento a elemento, y tienes el sistema de cuatro ecuaciones con dos incógnitas:

2x - 4 =  2

 x -  2 =  1, aquí haces pasaje de término, y queda: x = 3,

-4 - 2y = -2

-2 -  y = -1, aquí haces pasajes de términos, y queda: -1 = y;

luego, reemplazas los valores remarcados en las demás ecuaciones, y queda:

6 - 4 = 2, que es una igualdad Verdadera,

-2 - (-1) = -1, que es una identidad Verdadera;

por lo que puedes concluir que los valores remarcados son una solución válida para este problema

Espero haberte ayudado.

Observa que los resultados de cada dado son independientes de los resultados de los demás, y observa que la probabilidad de sacar un seis en un dado equilibrado es 1/6.

a)

p(6 6 6) = (1/6)*(1/6)*(1/6) = (1/6)³.

b)

Observa que tienes que la probabilidad de no sacar 6 en un lado equilibrado (observa que puedes sacar cualquiera de los cinco resultados: 1, 2, 3, 4 o 5) es 5/6.

p(no6 no6 no6) = (5/6)*(5/6)*(5/6) = (5/6)³.

c)

Observa que el suceso complementario es no sacar 6 en los tres dados, por lo que puedes plantear:

p(al menos un 6) = 1 - (5/6)³.

d)

Observa que para el primer dado tienes seis resultados posibles, para el segundo te quedan cinco (todos, menos el resultado del primer dado), y para el tercer te quedan cuatro (todos, menos los resultados de los dos primeros dados), luego, puedes plantear:

p(tres resultados distintos) = (6/6)*(5/6)*(4/6) = 1*(5/6)*(2/3) = 1*(5/3)*(1/3) = 5/9.

Espero haberte ayudado.

Muchas gracias , me has ayudado bastante y muy bien explicado.

Saludos.

Por favor, revisa tu enunciado, o envía una foto del mismo para que podamos ayudarte.

El enunciado es correcto, esta tal cual en mi hoja de tarea.