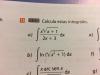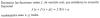Muchas gracias, me ha sido muy útil 

Observa que la recta r está presentada como intersección entre dos planos, de los que tienes sus ecuaciones cartesianas implícitas, y sus vectores normales: <3,a,-6a> y <-1,1,3>;

luego, puedes plantear que un vector director de la recta r es el producto vectorial entre los vectores normales:

u_r = <3,a,-6a> x <-1,1,3> = <9a,6a-9,a+3>.

Observa que tienes las ecuaciones cartesianas paramétricas de la recta s, y su vector director es: u_s = <-1,1,a>.

Luego, como las rectas r y s deben ser perpendiculares, puedes plantear que sus vectores directores también lo son, y que el producto escalar entre ellos es igual a cero:

u_r • u_s = 0, sustituyes las expresiones de los vectores, y queda:

<9a,6a-9,a+3> • <-1,1,a> = 0, desarrollas el producto escalar, y queda:

9a*(-1) + (6a-9)*1 + (a+3)*a = 0, resuelves en cada término, distribuyes en el tercer término, y queda:

-9a + 6a - 9 + a² + 3a = 0, reduces términos semejantes (observa que tienes cancelaciones), y queda:

a² - 9 = 0, haces pasaje de potencia como raíz, y tienes dos opciones:

1)

a = 3;

Luego, los vectores directores quedan: 

u_r = <27,9,6> y u_s = <-1,1,3>;

2)

a = -3;

Luego, los vectores directores quedan: 

u_r = <-27,-27,0> y u_s = <-1,1,-3>.

Espero haberte ayudado.

43)

Plantea la matriz ampliada del sistema:

a      1     -1      1

1      2      1      2

1      3     -1      0

Permutas la primera fila con la tercera, y queda:

1      3     -1      0

1      2      1      2

a      1     -1      1

A la segunda fila le restas la primera, a la tercera fila le restas la primera multiplicada por a, y queda:

1        3       -1        0

0       -1        2        2

0     1-3a     0        1

Luego, observa que tienes dos opciones, a partir de la expresión del segundo elemento de la tercera fila:

a)

1 - 3a = 0, de donde puedes despejar: a = 1/3;

luego reemplazas en la matriz remarcada, y queda:

1        3       -1        0

0       -1        2        2

0        0        0        1

y tienes, a partir de la tercera fila, que el sistema es incompatible.

b)

1 - 3a ≠ 0, de donde puedes despejar: a ≠ 1/3;

divides a la tercera fila de la matriz remarcada por (1-3a), y queda:

1        3       -1        0

0       -1        2        2

0        1        0    1/(1-3a)

a la segunda fila la multiplicas por -1, y queda:

1        3       -1        0

0        1       -2       -2

0        1        0    1/(1-3a)

a la primera fila le restas el triple de la segunda, a la tercera fila le restas la segunda, y queda:

1        0        5              6

0        1       -2            -2

0        0        2    (3-6a)/(1-3a)

luego, tienes que la matriz es escalonada, y tiene tres filas no nulas, por lo que el sistema es compatible determinado.

Espero haberte ayudado

45)

Multiplicas por la matriz identidad en el segundo término del primer miembro, y queda:

A² - 3*A*I 0 -2*I

Puedes extraer factor común izquierdo en el primer miembro de la ecuación, y queda:

A*(A - 3*I) = -2*I (*).

Luego, tienes una igualdad entre dos expresiones matriciales, por lo que puedes plantear la igualdad entre sus determinantes (observa que indicamos no n al orden de la matriz A), y queda:

det(A*(A - 3*I)) = det(-2*I)

Luego, aplicas la propiedad del determinante de un producto en el primer miembro, y del determinante de un múltiplo escalar de una matriz en el segundo miembro, y queda:

det(A) * det(A - 3*I) = (-2)ⁿ * det(I)

Luego, reemplazas el valor del determinante de la matriz identidad en el segundo miembro (recuerda que es igual a uno), resuelves, y queda:

det(A) * det(A - 3*I) = (-2)ⁿ (1)

Luego, observa que el segundo miembro es una potencia de -2, por lo que es distinto de cero, por lo que tienes que los dos factores del primer miembro son distintos de cero:

det(A) ≠ 0, por lo que tienes que la matriz A es invertible;

y también tienes:

det (A - 3*I) ≠ 0, por lo que tienes que la matriz (A - 3*I) es invertible.

Luego, haces pasajes de factores como divisores en la ecuación señalada (1), y queda:

det(A - 3*I)/(-2)ⁿ = 1/det(A),

por lo que tienes la expresión del determinante de la matriz inversa de la matriz A:

det(A^-1) = det(A - 3*I)/(-2)ⁿ.

Luego, multiplicas por  -1/2 en ambos miembros de la ecuación matricial señalada (*), y queda:

(-1/2)*A*(A - 3*I) = I

Ordenas factores en el primer miembro, y queda:

A * (-1/2)*(A - 3*I) = I

Luego, de acuerdo con la definición de matriz inversa, tienes:

A^-1 = (-1/2)*(A - 3*I).

Espero haberte ayudado.

Es muy muy complicada pero te dejo un link donde la explican paso a paso...
http://www.wolframalpha.com/input/?i=int+(arcsin((x%2F(x%2B1))%5E(1%2F2)))

En las páginas de la Olimpiada Matemática tienes resueltos éste y otros ejercicios similares.

Hola Antonio Benito García, gracias por todas tus repuestas y tu dedicación. No encuentro en la página de la Olimpiada Matemática la respuesta a éste problema, ¿podrías pasarme el link?

Gracias.

www.oei.es/historico/oim/revistaoim/numero30/ecuacionesfuncionales1.pdf