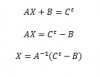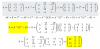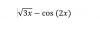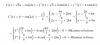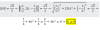-
Buenas, tengo dudas sobre este ejercicio de números complejos, alguien sabría solucionarlo? Gracias de antemano.
Antonio Silvio Palmitano
el 19/1/18Multiplicas por z en todos los términos de la ecuación que tienes en tu enunciado, y queda:
z2 + 1 = 2*cost*z, ordenas factores en el segundo miembro, haces pasajes de términos, y queda:
z2 - 2*z*cost = -1, sumas cos2t en ambos miembros, y queda:
z2 - 2*z*cost + cos2t = -1 + cos2t, factorizas en el primer miembro, extraes factor común en el segundo miembro, y queda:
(z - cost)2 = -1*(1 - cos2t), aplicas la identidad trigonométrica del cuadrado del seno en función del cuadrado del coseno en el segundo miembro, y queda:
(z - cost)2 = -1*sen2t, haces pasaje de potencia como raíz, y tienes dos opciones:
1)
z - cost = i*sent, haces pasaje de término, y queda:
z = cost + isent, luego, plantea las potencias del número complejo con la Fórmula de De Moivre:
zn = cos(nt) + isen(nt),
1/zn = z-n = cos(-nt) + isen(-nt) = aplicas las identidades trigonométricas del ángulo opuesto = cos(nt) - isen(nt);
luego, planteas la suma que tienes en tu enunciado:
zn + 1/zn = sustituyes expresiones = cos(nt) + isen(nt) + cos(nt) - isen(nt) = reduces términos semejantes (observa que tienes cancelaciones) = 2*cos(nt).
2)
z - cost = -i*sent, haces pasaje de término, y queda:
z = cost - i*sent = cos(-t) + i*sen(-t), luego, plantea las potencias del número complejo con la Fórmula de De Moivre:
zn = cos(-nt) + isen(-nt) = aplicas las identidades trigonométricas del ángulo opuesto = cos(nt) - isen(nt)
1/zn = z-n = cos(-n(-t)) + isen(-n(-t)) = cos(nt) + isen(nt);
luego, planteas la suma que tienes en tu enunciado:
zn + 1/zn = sustituyes expresiones = cos(nt) - isen(nt) + cos(nt) + isen(nt) = reduces términos semejantes (observa que tienes cancelaciones) = 2*cos(nt).
Por lo tanto, puedes concluir:
zn + 1/zn = 2*cos(nt).
Espero haberte ayudado.
-
3ºESO
1.- Descompón en producto de factores el polinomio, indicando cuáles son sus raíces:
a) P(x) = X4 + 3X3 − x2 − 3x ; b) P(x) = x3 − x2 − 12x ; c) P(x) = x3 − x2 + 4x − 4 ; d) P(x) = x3 − x − 6 ; e) P(x) = x5 − x4 − 5x3 − 3x2 ; f) P(x) = x3 − 7x2 + 14x − 8 ; g) P(x) = 3x4 + 15x2 ; h) P(x) = x4 − 16
Muchas Gracias.
Jordi García
el 19/1/18Te recomiendo que mires esta lista de UNICOOS sobre factorización y luego vuelvas a intentar a hacer el ejercicio.
Aún así te digo una pequeña explicación.
Tienes que igualar el polinomio a 0, resuelves la ecuación y las soluciones que te den son las raíces. Para expresarlo como producto de factores haz lo siguiente:
Supongamos que las soluciones de una ecuación te salen x1 = 2 y x2 = -3; pues el polinomio sería (x-2) · (x+3). Fíjate que si igualas cada paréntesis a 0, la solución del primer paréntesis es x1 = 2 y del segundo x2 = -3.
Saludos.
Antonio Silvio Palmitano
el 19/1/18Debes tener en cuenta el Teorema Fundamental:
"un polinomio de grado n admite a lo sumo n raíces reales, y admite exactamente n raíces en el campo de los números complejos);
y debes recordar los casos de factorización, la resolución de ecuaciones polinómicas cuadráticas por medio de la Fórmula de Baskara, y la Regla de Ruffini.
a)
El polinomio es de grado 4, por lo que admite a lo sumo cuatro raíces reales.
Puedes comenzar por extraer factor común, y queda: P(x) = x*(x3+3x2-x-3);
luego, extraes factores comunes por grupos en el agrupamiento, y queda: P(x) = x*( x2*(x+3) - 1*(x+3) );
luego, extraes factor común en el agrupamiento, y queda: P(x) = x*(x+3)*(x2-1);
luego, factorizas la resta de cuadrados perfenctos en el último factor, y queda:
P(x) = x*(x+3)*(x+1)*(x-1), que es la expresión factorizada del polinomio,
y sus raíces son: a = 0, b = -3, c = -1, d = 1, que son los valores de la variable x que anulan cada factor.
b)
El polinomio es de grado 3, por lo que admite a lo sumo tres raíces reales.
Puedes comenzar por extraer factor común, y queda: P(x) = x*(x2-x-12);
luego, factorizas el polinomio cuadrático en el agrupamiento por medio de la Fórmula de Baskara, y queda:
P(x) = x*(x+3)*(x-4), que es la expresión factorizada del polinomio,
y sus raíces son: a = 0, b = -3, c = 4, que son los valores de la variable x que anulan cada factor.
e)
El polinomio es de grado 5, por lo que admite a lo sumo cinco raíces reales.
Puedes comenzar por extraer factor común, y queda: P(x) = x2*(x3-x2-5x-3);
luego, observa que una de las raíces del polinomio en el agrupamiento es -1,
por lo que factorizas por medio de la Regla de Ruffini, y queda: P(x) = x2*(x+1)*(x2-2x-3);
luego, factorizas el polinomio cuadrático en el agrupamiento por medio de la Fórmula de Baskara, y queda: P(x) = x2*(x+1)*(x+1)*(x-3),
luego, reduces factores semejantes, y queda:
P(x) = x2*(x+1)2*(x-3), que es la expresión factorizada del polinomio,
y sus raíces son: a = 0, b = -1, c = 3, que son los valores de la variable x que anulan cada factor.
g)
El polinomio es de grado 4, por lo que admite a lo sumo cuatro raíces reales.
Puedes comenzar por extraer factor común, y queda:
P(x) = 3x2*(x2+5);
luego, observa que el polinomio en el agrupamiento no tiene raíces reales, por lo que tienes la expresión factorizada del polinomio en el campo de los números reales,
y su raíz es: a = 0, que es el único valor de la variable x que anula un factor;
luego, si has trabajado con números complejos, puedes igualar a cero la expresión del segundo factor, luego despejas, y tienes que la expresión factorizada del polinomio en el campo de los números complejos queda:
P(x) = 3x2*(x+5i)*(x-5i),
y sus raíces son: a = 0, b = -5i, c = 5i, que son los valores de la variable x que anulan factores.
c)
El polinomio es de grado 3,por lo que admite a lo sumo tres raíces reales.
Puedes comenzar por extraer factores comunes por grupos, y queda: P(x) = x2*(x-1) + 4*(x-1);
luego, extraes factor común, y queda:
P(x) = (x-1)*(x2+4);
luego, observa que el polinomio en el agrupamiento no tiene raíces reales, por lo que tienes la expresión factorizada del polinomio en el campo de los números reales,
y su raíz es: a = 1, que es el único valor de la variable x que anula un factor.
luego, si has trabajado con números complejos, puedes igualar a cero la expresión del segundo factor, luego despejas, y tienes que la expresión factorizada del polinomio en el campo de los números complejos queda:
P(x) = (x-1)*(x+2i)*(x-2i),
y sus raíces son: a = 1, b = -2i, c = 2i, que son los valores de la variable x que anulan factores.
d)
El polinomio es de grado 3, por lo que admite a lo sumo tres raíces reales.
Observa que 2 es una raíz del polinomio, luego factorizas por medio de la Regla de Ruffini, y queda:
P(x) = (x-2)*(x2+2x+3);
que es la expresión factorizada del polinomio en el campo de los números reales,
y su raíz es: a = 2, que es el único valor real de la variable x que anula un factor;
luego, si has trabajado con números complejos, aplicas la Fórmula de Baskara para factorizar el polinomio del agrupamiento, y queda:
P(x) = (x-2)*( x -(-1-√(2)i) )*( x -(-1+√(2)i) );
que es la expresión factorizada del polinomio en el campo de los números complejos,
y sus raíces son: a = 2, b = -1-√(2)i, c = -1+√(2)i, que son los valores de la variable x que anulan factores.
f)
El polinomio es de grado 3, por lo que admite a lo sumo tres raíces reales.
Observa que 2 es una raíz del polinomio, por lo que factorizas por medio de la Regla de Ruffini, y queda: P(x) = (x-2)*(x2-5x+4);
luego, factorizas el polinomio cuadrático del agrupamiento por medio de la Fórmula de Baskara, y qeuda:
P(x) = (x-2)*(x-1)*(x-4);
que es la expresión factorizada del polinomio,
y sus raíces son: a = 2, b = 1, c = 4, que son los valores de la variable x que anulan factores.
h)
El polinomio es de grado 4, por lo que admite a lo sumo cuatro raíces reales.
Factorizas la resta entre cuadrados perfectos, y queda: P(x) = (x2-4*(x2+4);
luego, factorizas la resta de cuadrados en el primer factor (observa que el segundo no tiene raíces reales), y queda:
P(x) = (x+2)*(x-2)*(x2+4);
que es la expresión factorizada del polinomio en el campo de los números reales,
y sus raíces son: a = -2, b = 2, que son los valores reales de la variable x que anulan factores;
luego, si has trabajado con números complejos, puedes igualar a cero la expresión del tercer factor, luego despejas, y tienes que la expresión factorizada del polinomio en el campo de los números complejos queda:
P(x) = (x+2)*(x-2)*(x+2i)*(x-2i),
y sus raíces son: a = -2, b = 2, c = -2i, d = 2i, que son los valores de la variable x que anulan factores.
Espero haberte ayudado.
-
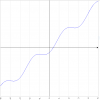
Necesito encontrar el crecimiento y decrecimiento de esta función. Tengo dudas para hallar x. ¿Cómo sería paso por paso? Muchas gracias!
Antonius Benedictus
el 19/1/18Carlos
el 19/1/18