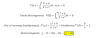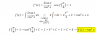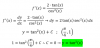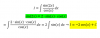-
en un bombo de loteria quedan cinco bolas. tres con numero par y dos con numero impar. si damos vueltas al bombo y extraemos dos bolas. ¿cual es la probabilidad de que la suma sea impar?
a) 1/2 b) 1/3 c) 2/5 d)3/5 e)3/4
Ángel
el 17/1/18C(5,2)= 5!/(2!*(5-2)!)= 5!/(2!*3!)= (5*4*3*2*1)/(2*1*3*2*1)= 120/12 = 10 combinaciones posibles
(impar1, impar2) = par
(impar1, par1) = impar
(impar1, par2) = impar
(impar1, par3) = impar
(impar2, par1) = impar
(impar2, par2) = impar
(impar2, par3) = impar
(par1, par2) = par
(par1, par3) = par
(par2, par3) = par
La probabilidad de que la suma x+y= (x,y) sea impar es casos favorables/ casos posibles = 6 casos favorables/ 10 casos posibles = 6/10 = 3/5
-
Neofito 007
el 17/1/18Antonius Benedictus
el 17/1/18Aleatorius
el 24/1/18La respuesta más precisa la encontré en otro lado, no obstante le doy 5 puntos a los dos participantes que respondieron educadamente e inteligentemente, y cuyas respuestas son adecuadas y dan una explicación útil y certera. Les agradezco muchos!!!
Respuesta buscada:
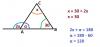
2x es el ángulo suplementario de alfa, por ende ambos suman 180. Y 180 también es la suma de los ángulos interiores del triángulo, de ahí sale la igualdad x+30+alfa=2x+alfa, que es igual a x+30=2x. De ahí sale x y luego usas ese valor para sacar alfa usando lo de que 2x+alfa=180 (como dije al comienzo).
En general, a los ángulos suplementarios de un ángulo interior se le llaman ángulo exterior y tienen el valor de la suma de los otros dos ángulos interiores. -
¿podéis ayudarme con ese ejercicio de integrales definidas?
Calcula la ecuacón de la recta tangente a la grafica de la función F(x)=
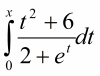 en el punto de abscisa x = 0.
en el punto de abscisa x = 0.Neofito 007
el 17/1/18Por el primer teorema fundamental del cálculo , la derivada de esa función es : F´(x) = ( x^2 + 6 ) / ( 2 +e^x )
La pendiente de la recta tangente en x = 0 es m = F´( 0) = ( 0^2 + 6 ) / ( 2 +e^0 ) = 6 / ( 2 +1 ) = 2
Ya tienes pendiente falta el punto reemplaza x = 0 en la función (que está dada por esa integral) y tendrías la integral desde 0 hasta 0 , esa integral es 0 ya que los límites de integración son iguales , por lo tanto F(0) = 0 , luego el punto es P( 0 , 0)
Tienes punto de paso P( 0 , 0) y pendiente m = 2 , la recta es y = 2x
-
Hola, ¿me podrían ayudar con estos ejercicios de integrales indefinidas?:
1- ∫ sen2x · sen3x dx
2- ∫ sen2x/cosx dx
3- ∫ x2 sen 3x
Muchas gracias.
Neofito 007
el 17/1/18Lo ha intentando alguno ?? a revisado las identidades trigonométricas ?
Mire la segunda es muy sencilla , basta saber que Sen2x = 2Senx Cosx , si a esto lo divides por Cosx se obtienes
Sen2x / Cosx = 2Senx , integrar esto último es elemental.
El tercero es por partes ( 2 veces ) , el primero quizá un poco más rebuscado pero con propiedades elementales se resuelve de manera inmediata .
Siempre primero intente , revise y si aún así no lo ha resuelto busque ayuda. -
Ángel
el 17/1/18Revisemos la continuidad desde -infinito hasta infinito, en todos los números reales:
Desde -infinito hasta 0.9999999...
Función lineal y=mx+n = 2ax+3 , que es continua por definición (una recta)
Desde 1.0000.....000001 hasta infinito
Función polinómica cuadrática y=mx2+nx =x2-bx , que es continua por definición (una parábola)
En el punto x=1
Tienen que coincidir los límites laterales lim(x->1-) 2a*x +3 = lim(x->1+) 1-b con el valor 3 = f(1)
2a*1 +3 = 3 = 12 -b*1 -----------> 2a+3=3=1-b -----> 2a+3=3 y 3=1-b ------> a=(3-3)/2 y b= 1-3 ------> a= 0 y b= -2
Por lo tanto, la función a trozos será continua en todo ℛ si a= 0 y b= -2 .
-
Antonio
el 17/1/18Calcule la derivada de esa funcion con la regla de la derivada de las divisiones. Una vez calculada esa, sustituyes donde haya x por el 0, y despeja. Para f'', derivas sobre la derivada primera y donde haya la x, lo sustituyes por 0 y sacas el resultado.
Derivada de la division: (Numerador derivado * Denominador sin derivar) - (Numerador sin derivar * Denominador derivado) todo ello dividido entre el Denominador elevado al cuadrado.
Ángel
el 17/1/18Ángel
el 17/1/18f´(x)= (-x2+2)/(x2+2)2
f´´(x)= ( (-2x)*(x2+2)2 - (-x2+2)*(2*(x2+2)*2x) )/ (x2+2)4 =0 ---------------> ( (-2x)*(x2+2)2 - 4x(-x2+2)*(x2+2) )/ (x2+2)4 =0
------------> ( (-2x)*(x2+2)2 - 4x(-x2+2)*(x2+2) ) = 0 -----------> ( (-2x)*(x4+4+4x2) - 4x(-x2+2)*(x2+2) ) = 0 ------------>
------------> -2x5-8x-8x3 - 4x(-x4+4) = 0 -----------> -2x5-8x-8x3 +4x5-16x = 0 ----------> 2x5-8x3-24x = 0 --------> x(x4-4x2-12)=0
Las soluciones de x las sacas de x(x4-4x2-12)=0
-----> x=0
-----> x4-4x2-12=0 ----cambio t=x2------> t2-4t-12=0 ----------> t=6 ,
t= -2----------> t=x2= 6 --------> x=±√6 -
Hola, buenas tardes, alguien podría ayudarme a demostrar por medio de inducción el siguiente ejercicio por favor:
Teniendo en cuenta la siguiente propiedad:
Y la siguiente definición:
Gracias de antemano!!, saludos.
Antonius Benedictus
el 17/1/18¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).