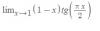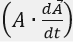-
Andres Sampayo
el 25/11/17
hola, alguien podira ayudarme con esta incognita, como puedo saber las componentes de un vector A(x,y,z)=xi+yj+zk, sabiendo 2 vectores por ejemplo
A(2)=2i-j+2k
A(3)=4i-2k-3k
-
Julio Rojas
el 25/11/17
demuestro el limite dado expresandolo como una funcion itnegral definida y evaluando , la integral ya realice todos los otros ejercicios pero este no se muy bien como demostrarlo -
Livaldo Ocanto
el 25/11/17 -
Carlos
el 25/11/17Es periodica la función p(x)= cos(2x)/(3+k'x) ? Según mis cálculos solo sería periódica si k=0 pero no estoy seguro.
Carlos
el 25/11/17 -
Juan
el 25/11/17Un función f: R->R continua y acotada, cómo demuestro que f(x)-x^3=0 tiene como mínimo una raíz real?
-
Andres Sampayo
el 25/11/17
como le calculo la integral?
Antonius Benedictus
el 25/11/17¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
Antonio Silvio Palmitano
el 26/11/17Vamos con una orientación.
Tomamos a modo de ejemplo la función vectorial de tres variables:
A = < p , q , r >,
cuyas componentes (p, q, r) son funciones con variable t, que son derivables y también integrables.
Luego, plantea la expresión de la función derivada primera:
dA/dt = < dp/dt , dq/dt , dr/dt >.
Luego, plantea el producto escalar:
A • dA/dt = < p , q , r > • < dp/dt , dq/dt , dr/dt > = p*dpdt + q*dq/dt + r*dr/dt.
Luego, plantea la integral:
∫ (A • dA/dt) = ∫ (p*dpdt + q*dq/dt + r*dr/dt) = p2/2 + q2/2 + r2/2 + C = (p2 + q2 + r2)/2 + C = |A|2/2 + C,
que es la solución general de la integral, que corresponde a una familia de funciones escalares con variable t.
Espero haberte ayudado.
-
Sara
el 25/11/17Calcula D, P y A10 de la matriz diagonalizable: ¿Cómo se haría?
A= 1 0 3
0 -2 0
2 0 0
Antonius Benedictus
el 25/11/17¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
Carlos
el 25/11/17porque la función y = 1/(x-2) en x=2 la discontinuidad es de segunda especie? no seria en todo caso una discontinuidad asintotica, es decir, de primera especie?
Antonius Benedictus
el 25/11/17
Carlos
el 25/11/17https://www.youtube.com/watch?v=5VcHZxch6H8 En este video, David dice que es de segunda especie. Que diferencia hay?
Antonius Benedictus
el 25/11/17No te compliques. Es cuestión de nomenclatura y varía de un texto a otro. La discontinuidad de 2ª especie se da cuando al menos uno de los límites laterales no existe (ni finito, ni infinito).
En cambio, otros textos incluyen el caso de los límites laterales infinitos.
