-
Antonius Benedictus
el 15/11/17Antonio Silvio Palmitano
el 15/11/17Observa que el signo * no indica el producto usual.
Plantea:
E = a2*√(b) = 8*2,
luego, comparas factores, y tienes:
a2 = 8, de donde tienes: a = √(8),
√(b) = 2, de donde tienes: b = 4.
Luego, plantea las expresiones logarítmicas:
a)
loga( 4√(b) ) = (1/4)loga(b) = reemplazas = (1/4)log√(8)(4) = (1/4)(4/3) = 1/3,
porque ( √(8) )4/3 = 22 = 4.
b)
logb(2a) = logb(2) + logb(a) = reemplazas = log4(2) + log4( √(8) ) =
= log4(2) + (1/2)log4(8) = 1/2 + (1/2)(3/2) = 1/2 + 3/4 = 5/4,
porque: 41/2 = 2 y 43/4 = √(8).
Luego, plantea la expresión de un enunciado, reemplazas, y queda:
E = 8*2 = log√(8)( 4√(4) ) + log4( 2√(8) ) = reemplazas valores remarcados = 1/3 + 5/4 = 19/12,
por lo que tienes que la opción A es la respuesta correcta.
Espero haberte ayudado.
-
-
Sea f la aplicación lineal de R3en R4 definida por f(x,y,z)= (x+z,2x+y,-y+2z,x+y-z). Dar dimensiones i bases de ker i Imf. Calcular la matriz asociada a f en la base B = {(1,-1,0),(1,0,-1),(1,0,1)} de R3 i en la base canonica de R4 .
Ayuda, no consigo resolverlo entero correctamente y tengo mañana el examen.
Antonius Benedictus
el 15/11/17¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
necronomicion00
el 15/11/17Rodrigo Ivan Saez
el 17/11/17El ker lo hallas igualando a cero y reduciendo el sistema y de alli sacas base y dimension, y la Im(f) es igual al espacio generado por las columnas de la matriz A de la transformacion, entonces para determinar base tomas la transpuesta de A y la reduces a la forma escalonada por reglones, los reglones que te queden seran una base.
la matriz de la transformacion la hallas asi: evaluas T(1,-1,0) , T(1,0,-1) , T(1,0,1) (con esto te aseguras de calcular la matriz con la base B del dominio, R3), y lo que te de, lo colocas como columnas de la matriz, y listo. La base del codominio (R4) te queda por definicion con base canonica.
Otro fuera el caso si te pidieran otra base en R4...
-
Hola Unicoos, me sale la segunda derivada igual que la primera derivada y no veo el fallo. Los resultados que me salen no son coherentes. Me podrían decir dónde está el fallo? Muchas gracias
-
Hola estoy intentando hacer un límite pero no me sale, me gustaría saber qué pasos seguir,es este :
Limite de x tendiendo a cero= 2xcos(lnx)
Antonio Silvio Palmitano
el 15/11/17Vamos con una orientación:
observa que la expresión del argumento es una multiplicación,
y que el primer factor (2x) tiende a 0, y que el segundo factor ( cos(lnx) ) está acotado entre -1 y 1,
por lo tanto, tienes que el límite de tu enunciado es igual a 0.
Espero haberte ayudado.
-
Llego a plantear ecuaciones
x2 -6x = x
3x+3y= 3
-2x-2y = -2
-6+y2 = y
Resuelvo x y me da 3 y -2, resuelvo y y me da 3 y -2. ¿ Y no se cuál es la solución?
Neofito 007
el 15/11/17Pues es muy sencillo , ambas son soluciones osea que son 2 matrices que cumplen dicha condición .
Matriz A1 , para x = 3 , y = -2
Matriz A2 , para x = -2 , y = 3
Esto es así :
* De la primera ecuación se encuentra x = 3 ó x = -2
* Se trabaja para x=3 y se reemplaza en la segunda (o en la tercera) y se calcula " y " que se obtiene y = -2
* Se verifica que este valor de " y "satisface las otras 2 ecuaciones .
* Si satisface entonces es solución , luego el par ordenado (x,y) = (3 , -2) es solución.
Similar se toma x = -2 y se realiza el proceso anterior , dado que verifica entonces se tiene (x,y) = ( - 2 , 3) es solución
-
Antonio Silvio Palmitano
el 15/11/171)
Plantea la condición para las raíces (consideramos que a es la incógnita):
a5 - a3b2 - a2b3 + b5 = 0, extraes factores comunes por grupos, y queda:
a3(a2 - b2) - b3(a2 - b2) = 0, extraes factor común, y queda:
(a2 - b2)(a3 - b3) = 0;
luego, por anulación de un producto, tienes dos opciones:
a)
a2 - b2 = 0, haces pasaje de término, y queda:
a2 = b2, haces pasaje de potencia como raíz, y tienes dos raíces:
a = -b y a = b;
b)
a3 - b3 = 0, haces pasaje de término, y queda:
a3 = b3, haces pasaje de potencia como raíz, y queda:
a = b, que es una de las dos raíces remarcadas.
Por lo tanto, puedes concluir que las raíces del polinomio:
P(a) = a5 - a3b2 - a2b3 + b5, son: a = -b y a = b.
Espero haberte ayudado.
Antonio Silvio Palmitano
el 15/11/17Tienes la inecuación:
(x2 - 4) / (x2+3x) < 0,
luego, factorizas en el numerador y en el denominador, y queda:
(x + 2)(x - 2) / x(x + 3) < 0,
luego, tienes dos opciones:
a)
si el denominador es positivo: x(x + 3) > 0, que corresponde al intervalo: (-∞,-3) ∪ (0,+∞) (1);
haces pasaje de divisores como factores (observa que no cambia la desigualdad, y queda:
(x + 2)(x - 2) < 0, que corresponde al intervalo (-2,2) (2);
luego, plantea la intersección entre los intervalos señalados (1) (2), y queda:
Ia = [ (-∞,-3) ∪ (0,+∞) ] ∩ (-2,2) = (0,2);
b)
si el denominador es negativo: x(x + 3) < 0, que corresponde al intervalo: (-3,0) (3);
haces pasaje de divisores como factores (observa que si cambia la desigualdad, y queda:
(x + 2)(x - 2) > 0, que corresponde al intervalo (-∞,-2) ∪ (2,+∞) (4);
luego, plantea la intersección entre los intervalos señalados (3) (4), y queda:
Ib = [ (-∞,-2) ∪ (2,+∞) ] ∩ (-3,0) = (-3,-2);
luego, planteas la unión de los intervalos obtenidos en las opciones, y tienes el intervalo solución:
S = Ib ∪ Ia= (-3,-2) ∪ (0,2).
Espero haberte ayudado.












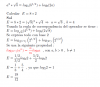


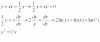






















 Alguien me puede ayudar con este ejercicio porfavor
Alguien me puede ayudar con este ejercicio porfavor

