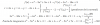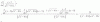-
Adrián
el 16/11/17
Ayuda con este ejercicio de espacios vectoriales porfavor.
Muchisimas gracias
Antonius Benedictus
el 16/11/17Rodrigo Ivan Saez
el 16/11/17es lo mismo que se aplica con vectores en R^n como en los videos, solo que los vectores son los coeficientes de los polinomios. En tu caso, para la matriz de B a B' por ejemplo, debes hallar combinaciones lineales de cada uno de los polinomios de la base B, en funcion de B':
x = a(1) + b(1+x) + c(x^2)
pero esto es una ecuacion con 4 incognitas, como hallamos las otras 2 ecuaciones? pues este polinomio se cumple para todo x perteneciente a los reales, entonces si evaluamos para x=-1, x=0, x=1 obtenemos:
-1 = a+c
0=a+b
1=a+2b+c
y eso es un sistema, te dara un vector (a,b,c)
Lo mismo haces para:
1+x^2 = d(1) + e(1+x) + f(x^2)
que te dara un vector (d,e,f),
y tambien para:
x+x^2 = g(1) + h(1+x) + i(x^2)
que te dara un vector (g,h,i)
Y esos 3 vectores los colocas como columnas de una matriz, que sera tu matriz de cambio de base de B a B':
a...d...g
b...e...h
c...f....i
Entonces por ejemplo si tienes un polinomio en terminos de la base B:
t(1) + u(1+x) + v(x^2)
y lo quieres transformar a un polinomio en base B', multiplicas la matriz anterior por el vector columna (t,u,v), y te dara un vector con los coeficientes del mismo polinomio pero en términos de la base B'
Para la matriz de B' a B puedes hacer el mismo procedimiento (al revés), o simplemente hallar la inversa.
En cuanto al polinomio que te dan, tienes que hallar nuevas matrices de cambio de base, una matriz de Bc a B , y otra matriz de Bc a B'
donde Bc=base canonica -> {1,x,x^2}
-
Eric
el 16/11/17 -
daniel
el 16/11/17
me ayudan con el ejercicio e
Hallar laplace inversa.... :
Antonius Benedictus
el 16/11/17¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
Ani Levi
el 16/11/17Buenas, bueno tengo una duda con el apartado B), me podrían ayudar ¿se haría el mismo proceso que el apartado a)?. Gracias
-
Elisa guti
el 16/11/17me podeis ayudar con este ejercicio , es de 2 bachillerato , por favor
-
Elisa guti
el 16/11/17 -
Luis Vila Perez
el 16/11/17matrices cuadradas y determinantes de orden dos y tres
Me gustaría aprender a identificar en el plano y en el espacio los conceptos intuitivos que representan una matriz y determinante de orden 2, o una matriz y determinante de orden tres.
También, igualmente, explicarme geométricamente para los casos anteriores cuando la cupla o terna represente una línea en el plano o en el espacio respectivamente. Por ejemplo en el caso de una matriz de orden tres cuando las filas sean de la forma : ax by cz donde a,b,z son números reales , y el resto variables x , y y z también de ℛ.
Entender intuitivamente las transformaciones en matrices equivalentes mediante transformaciones de las mismas a matriz triangular, sumas de cantidades linealmente dependientes y conceptos relacionados.
Hacerme a una idea intuitiva de lo que estoy haciendo en base a la resolución de sistemas de ecuaciones de primer grado con matrices en base a lo que las ecuaciones que trato de resolver representan geométricamente.
Y, en fin, algún enlace que me ilumine sobre estas ideas intuitivas siempre limitadas a el orden 2 y el orden 3.
Si el resultado de un determinante de orden dos o tres tiene alguna significación geométrica.
Gracias
-
carmela
el 16/11/17 -
Angelica
el 16/11/17 -
Francisco Bk Gtz
el 16/11/17tengo una duda con el siguiente ejercicio al resolverlo A me da 0.6695 y B 0.12 es correcto el resultado? Saludos.
Antonius Benedictus
el 16/11/17¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
